Productive Rage

27 March 2018

Learning F# via some Machine Learning: The Single Layer Perceptron

TL;DR

I know C# well and I want to learn F#. I want to wrap my head about some of the underlying algorithms that enable the machine learning that seems so prevalent in the world today (voice recognition, computer vision, sales prediction, semantic analysis, translation). I'm going to try to do both together and prove to myself that I have a good understanding of them both by writing about it.

The lure of F#

For a few years now, I've been wanting to have a proper crack at learning F#. There's a lot about it that sounds very appealing - immutability-by-default and better representation / handling of null values while still being able to use Visual Studio and use the .NET framework library (as well as other .NET assemblies). I've tried a couple of times in the past but without any concrete project to work on, I find that I struggle to motivate myself without a target to work towards that is more tangible than "feel like I've learned a bit of a new language".

To address this, I've decided to combine learning-some-F# with learning-some-machine-learning-basics so that I have a more solid goal. As I go, I thought that I'd write a few posts about the process for two reasons; firstly, being able to explain something clearly is a good indicator that you understand it yourself and, secondly, there is a chance (admittedly slim!) that this might be useful to someone else in a similar position to me, who is familiar with C# and wants to get to grips with F# - I wouldn't even consider myself intermediately competent yet and so I'm still encountering the pain points of being an F# beginner and seeing how I deal with them might be helpful to others.

Last year, I wrote Face or no face (finding faces in photos using C# and Accord.NET), which classified image regions using a linear support vector machine. This was technically a machine learning solution but it's only one particular algorithm and there are limitations to the sorts of problem that it can tackle. I want to work up to implementing a Back-Propagation Neural Network that will categorise hand written digits (0-9) but I'm going to start a little simpler.

While trying to decide how I was going to get started, I read (or scan-read, in many cases, if I'm being honest) what felt like hundreds of articles about neural networks. One of the issues with trying to learn something like this through the research of others is that the people writing about it already have a level of knowledge far above my own on the matter and it feels like there is a lot of knowledge that it assumed that the reader will have. Another issue is that there is often maths involved that can seem sufficiently complicated that it is off-putting. In my posts, I'm going to try to keep things as simple as possible (which may well mean brushing some "whys" under the carpet - leaving it as an exercise to the reader to find out more from other people, once the basics are understood). One series of posts that I did find very approachable, though, was on a site "Robosoup" - which is for a consultancy based in London that specialise in machine learning. The first post in the series is "The Single Layer Perceptron C#" and I'm actually going to start with some of the code there and the example data. I'm going to try to explain things my own way but much of the content here will owe a debt to that Robosoup article (I got in touch with John Wakefield at Robosoup and he said that he was happy for me share his code - rest assured that I'm not just stealing it without asking for permission first!).

The Single Layer Perceptron

The concept of an "artificial neural network" is, essentially, that there is a system of neurons that are connected together and that have a series of inputs that send signals into the system and which eventually get (somehow) transformed into a series of outputs. Each output represents a particular result. If, for example, the neural network was intended to categorise images then the inputs will all be derived from the image data in some way and there may be an output for "dog" and an output for "cat" and these output will end up with a stronger or weaker signal depending upon the input data. The connections between the neurons will have different "weights" and so different input values will somehow result in different outputs. These different weights will have to calculated as part of the network's "training". This sort of description is often accompanied by complicated-looking diagrams such as this:

(Taken from Cesar Harada's Flickr under license conditions)

This raises a lot of questions and feels like far too complicated a place to start! (Though, in later posts, I will be talking about multi-layered multi-output neural networks similar to what is shown above).

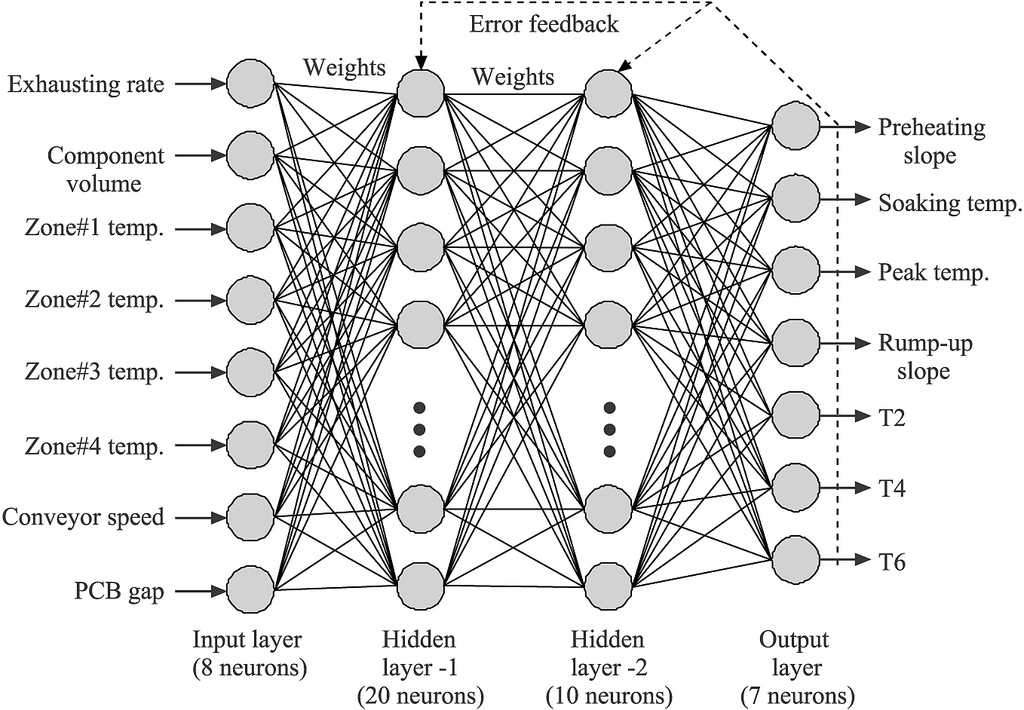
The "Single Layer Perceptron" is simpler - it only has one input "layer" and one output "layer", where a layer is a list of "neurons". A neuron is something that takes an input value (a value from -1 to 1), multiplies it by a "weight" (also a value from -1 to 1) and then passes that value onto every node that it is connected to in the layer ahead of it. Pretty much the simplest possible network imaginable that would fit this description would be just two neurons in the input layer and a single neuron in the output layer. Like this:

Now this might almost seem too simple! Can this really do anything useful? Well, actually, it's entirely possible to configure a network like this to act as a classifier for any data that is "linearly separable" in as many dimensions as there are inputs. This is already sounding like mumbo jumbo, so I'll go over those terms..

A "classifier" will look at its inputs and give a yes/no answer (for example, an "is this a cat?" classifier might look at a photograph and report whether there appears to be a cat in it or not).

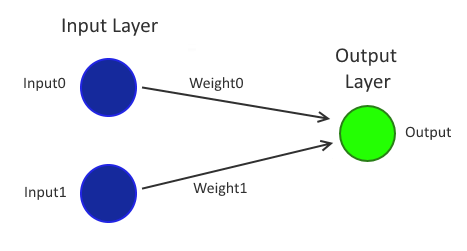
"Linearly separable" is simplest to understand in 2D - if the data is plotted on a graph then it's "linearly separable" if it's possible to draw a straight line across the graph that puts all of the values for "yes" lie on one side and all inputs for "no" lie on the other side. When I wrote about linear support vector machines, I talked about a fictional decision history for a manager, where they would give the go-ahead (or not) to a new feature based upon how much of it could be billed to Clients and what strategic value it had to the company.

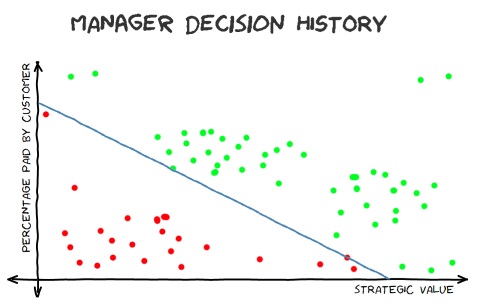
This data is linearly separable because it's possible to draw a line on the graph where all of the data above gets a "yes" response and all of the data below gets a "no".

Some data sets will not fit this model and so are not linearly separable. That won't make it impossible to classify using a neural network but it will make it impossible for a perceptron to classify (without some form of processing of the data before classification - which is out of the scope of what I want to cover today).

2D data like this would involve a perceptron with two inputs. 3D data that is linearly separable would have all of its data points separable by a plane in the 3D space - all points on one side would be "yes" and all points on the other would be "no"; this data would involve a perceptron with three inputs.

While it's not as easy to envisage this in more dimensions, the same principle holds. For this sort of multi-dimensional data, the additional dimensions tend to be additional measurable factors that are thought to have affected the outcome (for example, maybe the manager in the example above is predictably less likely to give the go-ahead to features on Monday and Tuesday because they're always snowed under with emails for those first two days of the week and they're less likely to sign off on things when they're hungry; that would mean that there would be four dimensions to consider, which would be "amount of cost that can be put onto Clients", "strategic value of the work", "day of the week" and "time since last ate" - these four dimensions would require a perceptron with four inputs to model the data).

Training a perceptron

I said above that it's possible to configure a network to act as a classifier for linearly separable data. All that is required to configure the network is to assign the weight0 and weight1 values (at least, that is the case for 2D data - since each input has its own weight value then 2D data requires two inputs but if the input is three dimensional then there will be three weight values that must be set and if there were four dimensions then there would be four weight values, etc..). When it is correctly configured, it will be possible to apply any values to the input neurons and to get a single output value. If this output value is higher than a particular threshold then the output will be considered a positive response and otherwise it will be considered a negative response.

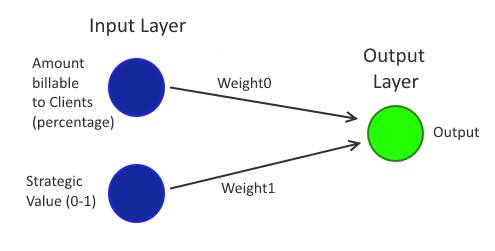
Returning to the Manager Decision data, one of the inputs will be for the "amount of cost that can be put onto Clients" while the other will be the "strategic value of the work". For the data and the code that I'm going to look at further down, all inputs and outputs are in the 0-1 range (this is convenient enough for "amount of cost that can be put onto Clients" but it may be more difficult in the real world to fit all features into a 0-1 range for "strategic value of the work" - but since that data is just a fictional example, we don't need to worry about that too much).

The question, then, is how should we determine the weights for each neuron? This is where the "machine learning" part comes into it. What we're going to do is "train" a network by using historical data.

At its essence, the way that a trained network like this is produced is by -

1. Setting all of the weights to be random values between 0 and 1
2. Passing all of the historical data (aka "training data") through it and, for each "pattern" (which is the name given to a series of inputs)

• Calculating the "local error" (the error for that particular pattern)
• Adjusting the weights based upon this local error

1. Taking the "total error" or "global error" (the sum of all of the local errors from the training data) and either finding that it is less than a predetermined threshold (in which case the network training is considered complete - hurrah!) or going back to step 2

There are a lot of things to consider there - what precisely are the "local errors", how are the weights adjusted each iteration and what threshold should we stop at? Let's work through each of those in order..

The local error for a particular pattern is how far away the output of the network is from the expected result. Since all of the input data has a yes/no expected output, we'll translate "yes" into 1 and "no" into 0. For each pattern, we take its inputs and set the input neurons with those values. Then we calculate the output for the network (by multiplying the first input by the first weight and the second input by the second weight and then adding those two values together). Then we compare this output value to the expected 1 or 0 - so, if we get 0.3 as the output value for the first pattern and we expected 1 then that's an error of 0.7 (since 0.3 is 0.7 away from the expected value of 1). If we get 0.6 for the output value for the second pattern and we expected 0 then that's an error of 0.6 (since 0.6 is 0.6 away from the expected value of 0).

In order to adjust the weights after each pattern has been run through the network, a fairly simple equation is used - each new weight is calculated using:

weight[i] = weight[i] + (learningRate * localError * patternInput[i])

For this network, there are only two inputs and so there will only be two values for "i".

The "learning rate" is a value between 0 and 1 that determines how quickly the weights change as the network is trained. Clearly, a value of 0 would mean that the weights don't change each iteration, which would be useless. The larger the value of the learning rate, the more that the weights will be adjusted each iteration - however, larger is not always better because the adjustments may swing too far each time and, instead of slowing homing in on a well-trained network, the weights may alternate back and forth and never significantly improve. In the example code that I'm going to look at, I'm using a learning rate of 0.1* but this is a value that you may wish to try playing with when experimenting with training - there seem to be many guidelines when it comes to machine learning and many sensible approaches to classes or problem but there aren't always hard and fast rules for all of the variables and there are often things to tweak here and there that may affect how quickly you get a result (or if you get one at all).

* (To be honest, I've "decided" to use a learning rate of 0.1 because much of the initial C# code below comes from the Robosoup article that I mentioned earlier and a 0.1 learning rate is used there!)

The acceptable "global error" is another "tunable parameter" in that a higher acceptable threshold should mean that training will complete more quickly but also that the resulting network will be less accurate. On the other hand, it may be impossible to train a network (particularly so simple a network as a single perceptron) to match all of the training data perfectly and so a reasonable threshold must be accepted. In the example code below, a network that perfectly matches the training data is possible and won't take long to train and so we'll aim for a zero global error.

I'm not going to go into any more detail about how you may set these tunable parameters (learning rate and global error threshold) because there's a lot of material to cover and I want to try to stick to practical concepts and code (and because I'm still not very confident that I've got a great system for deciding them!).

Input bias

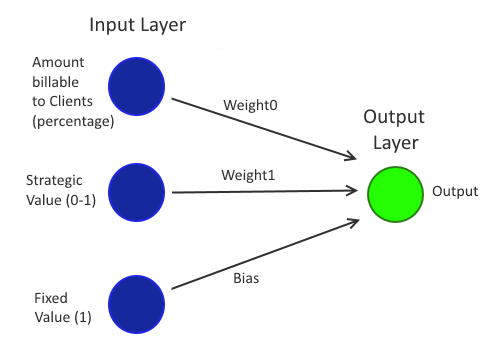
Using the training method described above, you will always get a line that cuts through the data at the point (0, 0). This would not work for the "Manager Decision History" graph because there is no way that a line starting at the bottom left of the graph could correctly cut through the data with all of the red points on one side and all of the green points on the other (on that graph all values are 0-1 and so the bottom left is the 0, 0 point).

A way to address this is to introduce an additional "bias" value. This is effectively like adding an additional neuron whose input value is always one and that has its own weight, just like every other input. Every time that a pattern is passed through the system while it is being trained, when the weights are adjusted, the bias should also be adjusted using the following formula:

bias = bias + (learningRate * localError)

(The formula is basically the same as the weight-adjusting formula except that the "patternInput[i]" value is removed because the bias neuron's input value is always 1)

This bias value means that the line that separates the yes/no values no longer has to go through (0, 0) but it has no other effect on training process, other than there being more slightly more work to do (although, without it, we wouldn't be able to get an answer for many sets of data - so it's not really more work at all!).

I've just said that it would not be possible to train a simple network of this form for some data sets without a bias.. which begs the question "for what data sets should a bias node be introduced?" - I think that it makes sense to always include one since, presumably, you don't know what solution the neural net should produce and so you don't know whether or not it would strictly be necessary to have a bias. So it's better to err on the safe side. If the data does not require a bias then the trained network should end up with a small (ie. close to zero) bias value and it will have little impact.

(This "input bias" is very different to moral biases that can creep into machine learning predictions due to biases, that are often unintentionally included, in the training data - see "Forget Killer Robots—Bias Is the Real AI Danger")

From C# to F#..

The format that I intend to follow for these posts is roughly as follows:

1. Talk about the theory (we've already done that today!)
2. Look at some fairly standard C# code
3. Look at making the C# code more functional by removing variable mutations (including loops)
4. Rewrite the "functional C#" in F#

As an F# beginner, this is the approach that I've been using for trying to learn it - until I've internalised it further, it still feels like a big ask to take regular C# and rewrite it into idiomatic F# and so the "functional C#" stage helps me a lot. The syntax of F# is not that big of a deal but thinking in (functional) F# is still something that I'm working towards.

(It's worth noting that, for me, getting my head around F# and functional programming is the priority. Much of the C# that we'll be looking will be doing in-place mutations - which, arguably, is a good model for doing the processing that we'll be looking at when it's done on a single thread - and since we'll be moving to using immutable structures then there is a good chance that the performance will be worse in the final F# code. If that turns out to be the case, though, then I'm not going to worry about it. I think that performance concerns are for when you have a better grasp of the technology that you're working with and I'm not there yet with F# - so I don't mind if I end up with worse-performing code in the context of this post so long as I've learned a lot from writing it!)

// Code slightly modified from that at
// http://www.robosoup.com/2008/09/the-single-layer-perceptron-c.html
public static class Perceptron
{
  public static void Go(Random r)
  {
    // Load sample input patterns and expected outputs
    var trainingData = new[]
    {
      Pattern(0.08, 0.94, true), Pattern(0.13, 0.95, true), Pattern(0.28, 0.66, true),
      Pattern(0.3, 0.59, true), Pattern(0.31, 0.51, true), Pattern(0.34, 0.67, true),
      Pattern(0.34, 0.63, true), Pattern(0.36, 0.55, true), Pattern(0.38, 0.67, true),
      Pattern(0.4, 0.59, true), Pattern(0.4, 0.68, true), Pattern(0.41, 0.5, true),
      Pattern(0.42, 0.53, true),  Pattern(0.43, 0.65, true), Pattern(0.44, 0.56, true),
      Pattern(0.47, 0.61, true), Pattern(0.47, 0.5, true), Pattern(0.48, 0.66, true),
      Pattern(0.52, 0.53, true), Pattern(0.53, 0.58, true), Pattern(0.55, 0.6, true),
      Pattern(0.56, 0.44, true), Pattern(0.58, 0.63, true), Pattern(0.62, 0.57, true),
      Pattern(0.68, 0.42, true), Pattern(0.69, 0.21, true), Pattern(0.7, 0.31, true),
      Pattern(0.73, 0.48, true), Pattern(0.74, 0.47, true), Pattern(0.74, 0.42, true),
      Pattern(0.76, 0.34, true), Pattern(0.78, 0.5, true), Pattern(0.78, 0.26, true),
      Pattern(0.81, 0.48, true), Pattern(0.83, 0.32, true), Pattern(0.83, 0.28, true),
      Pattern(0.85, 0.07, true), Pattern(0.85, 0.45, true), Pattern(0.88, 0.4, true),
      Pattern(0.89, 0.92, true), Pattern(0.9, 0.33, true), Pattern(0.91, 0.05, true),
      Pattern(0.92, 0.44, true), Pattern(0.95, 0.94, true), Pattern(0.96, 0.08, true),

      Pattern(0.02, 0.76, false), Pattern(0.06, 0.22, false), Pattern(0.07, 0.16, false),
      Pattern(0.09, 0.43, false), Pattern(0.1, 0.08, false), Pattern(0.14, 0.07, false),
      Pattern(0.15, 0.23, false), Pattern(0.17, 0.18, false), Pattern(0.17, 0.11, false),
      Pattern(0.21, 0.28, false), Pattern(0.22, 0.17, false), Pattern(0.25, 0.09, false),
      Pattern(0.28, 0.28, false), Pattern(0.28, 0.27, false), Pattern(0.29, 0.22, false),
      Pattern(0.29, 0.29, false), Pattern(0.3, 0.29, false), Pattern(0.31, 0.14, false),
      Pattern(0.33, 0.19, false), Pattern(0.33, 0.06, false), Pattern(0.39, 0.15, false),
      Pattern(0.52, 0.1, false), Pattern(0.65, 0.07, false), Pattern(0.71, 0.1, false),
      Pattern(0.74, 0.05, false)
    };

    // Randomise weights
    var weights = new[] { r.NextDouble(), r.NextDouble() };
    var bias = 0d;

    // Set learning rate
    var learningRate = 0.1;
    var iteration = 0;
    double globalError;
    do
    {
      globalError = 0;
      for (var p = 0; p < trainingData.Length; p++)
      {
        // Calculate output
        var inputs = trainingData[p].Item1;
        var output = Output(weights, bias, inputs[0], inputs[1]) ? 1 : -1;

        // Calculate error
        var expected = trainingData[p].Item2;
        var localError = (expected ? 1 : -1) - output;
        if (localError != 0)
        {
          // Update weights
          for (var i = 0; i < 2; i++)
          {
            weights[i] += learningRate * localError * inputs[i];
          }
          bias += learningRate * localError;
        }

        // Convert error to absolute value
        globalError += Math.Abs(localError);
      }
      Console.WriteLine("Iteration {0}\tError {1}", iteration, globalError);
      iteration++;
    } while (globalError != 0);

    Console.WriteLine();
    Console.WriteLine(
      $"Final weights: {weights[0]}, {weights[1]}, Bias: {bias} => Error: {globalError}"
    );

    // Display network generalisation (note: the "Manager Decision" data has input values that
    // are all in the range 0-1 in both dimensions and so we will only look at values in this
    // range in this preview here)
    Console.WriteLine();
    Console.WriteLine("X,\tY,\tOutput");
    for (double x = 0; x <= 1; x += .25)
    {
      for (double y = 0; y <= 1; y += .25)
      {
        var output = Output(weights, bias, x, y);
        Console.WriteLine("{0},\t{1},\t{2}", x, y, output ? "Yes" : "No");
      }
    }
    Console.WriteLine();
  }

  private static bool Output(double[] weights, double bias, double x, double y)
  {
    var sum = (x * weights[0]) + (y * weights[1]) + bias;
    return (sum >= 0);
  }

  /// <summary>Helper for initialising training data</summary>
  private static Tuple<double[], bool> Pattern(double x, double y, bool output)
  {
    return Tuple.Create(new[] { x, y }, output);
  }
}

This code is fairly straightforward and it goes through the steps that I described before:

1. Set weights to be random values and the bias to be zero
2. Take each training data entry's input and calculate the output using the current weights (and bias), adjusting the weights (and bias) if the calculated output did not match the expected output
3. Compare the total error against a threshold (of zero) and go back to step 2 if it's too high

The way that I'm going to change this code from "regular" (I would call it "object oriented" C# but the code shown here is probably closer to being "procedural") to "functional*" C# is by looking for things that would seem out of place in functional code and replacing them.

* ("functional" is often interpreted as meaning that you avoid side effects and avoid mutation - we can argue about that definition another day if you like but it's a good enough place to start for now!)

Immediately, the following things jump out at me:

1. Variables whose values are explicitly changed during processing (eg. "iteration" and "globalError")
2. Variables whose values change as part of looping constructs (eg. "i", "x" and "y")
3. The do..while loop will not be useful if values are not to be mutated with it and so that will need to be replaced with something else

I suppose the question, then, is how can we possibly write code like this without changing / mutating / updating values?

The first thing to recognise is that LINQ made a more functional style of processing much more mainstream within C# and seem less alien. Before LINQ, if you had an array of values and you wanted an array containing the squares of these values (contrived example, I know, but bear with me) then you may well have achieved this in a fairly procedural manner - eg.

var values = new[] { 1, 2, 3 };
var squaredValues = new int[values.Length];
for (var i = 0; i < values.Length; i++)
  squaredValues[i] = values[i] * values[i];

Each time the loop is executed, the value of "i" changes and the "squareValues" array is updated.

Until the for loop has been fully executed, the "squaredValues" array is only partially initialised.

Within the loop, it's technically possible to change the value of "i" and move it backwards or forwards (such as by throwing in a bonus "i++" to keep future code maintainers on their toes) and this can be the cause of potential coding errors in loops more complicated than the one shown here.

Since all we want to do is transform every single value in one array and create a new array from the results, it would be nice if we could be more descriptive in what we are trying to do and to remove some "book keeping" (such as tracking the "i" value using the for loop). This is what would happen if LINQ was used to perform the same work -

var values = new[] { 1, 2, 3 };
var squaredValues = values
  .Select(value => value * value)
  .ToArray();

Note that there is no mutation occurring here. Each time that the lambda that is passed to the "Select" method is called, a new "value" reference is created (unlike "i", which was a single variable shared across each iteration of the loop).

This is one technique that will be useful to remove mutation from code.

Another is the "Aggregate" method for enumerating a list of items and reducing it to a single reference. To try to illustrate; if I had a collection of words and I wanted to get the total number of words and the total number of letters then I might write procedural code like this:

static void ShowLetterAndWordCount(IEnumerable<string> words)
{
  var numberOfLetters = 0;
  var numberOfWords = 0;
  foreach (var word in words)
  {
    numberOfLetters += word.Length;
    numberOfWords++;
  }
  Console.WriteLine("Total number of letters: " + numberOfLetters);
  Console.WriteLine("Total number of words: " + numberOfWords);
}

.. or I could achieve the same thing without any mutating variables by using the following code:

static void ShowLetterAndWordCount(IEnumerable<string> words)
{
  var summary = words.Aggregate(
    seed: new { NumberOfLetters = 0, NumberOfWords = 0 },
    func: (valueSoFar, nextWord) => new
    {
      NumberOfLetters = valueSoFar.NumberOfLetters + nextWord.Length,
      NumberOfWords = valueSoFar.NumberOfWords + 1
    }
  );
  Console.WriteLine("Total number of letters: " + summary.NumberOfLetters);
  Console.WriteLine("Total number of words: " + summary.NumberOfWords);
}

What "Aggregate" does is it takes a "seed" value and the first value of the list of items and combines them using the "func" lambda. It then takes this result and combines it with the second value of the list, also using the "func" lambda. It will then take this result and combines it with the third value of the list, etc.. until one final combined value is returned. In the code above, I've used an anonymous type for the seed (and so the final "summary" reference will also be an instance of that anonymous type and so have "NumberOfLetters" and "NumberOfWords" properties) but the seed can be a class or a primitive or any type that you need.

All of the "book keeping" required by the Aggregate method is handled by the method itself - there is no loop variable to worry about and there are no variables outside of the loop (such as "numberOfLetters" and "numberOfWords") that must be tracked. You need only to tell it what the initial "seed" value should be and how it should combine the "value so far" with a single item from the input list.

This is the advantage that it has over the procedural version (which may initially appear "less complicated") - you only need to consider what actually happens within a single operation and you don't have to look after any variables that must be maintained across the entire loop (which was the case with "numberOfLetters" and "numberOfWords" in the first version).

At its core, this means that the scope of variables is reduced and when they don't change (ie. they are immutable) there are less moving parts for you to mentally consider when trying to reason about any particular line of code.

I'm finding that the F# version of Aggregate (called "fold") is a very powerful and useful technique and so having a good grasp on how it works is very useful. Just to make it extra clear (apologies if this is belabouring the point but Aggregate doesn't, in my experience, tend to be commonly used in C# and so it may not be familiar to some), here's another example:

var values = new[] { 1, 2, 3, 4, 5 };
var sumOfValues = words.Aggregate(
  seed: 0,
  func: (valueSoFar, value) => valueSoFar + value
);

This will return 15 because it will just add all of the values together. It begins with a seed value of 0 and adds it to the first value (which is 1) to get 1. It then adds this "value so far" to the second value (which is 2) to get 3. It adds this to the third value (which is 3) to get 6 and adds this to the fourth value (which is 4) to get 10 and adds this to the fifth value (which is 5) to get 15.

Not a particularly useful piece of code - and one that could have been written more clearly as:

var values = new[] { 1, 2, 3, 4, 5 };
var sumOfValues = words.Sum();

.. but hopefully it reinforces how the Aggregate method operates on data. And hopefully it makes it clear how powerful Aggregate can be because so many other operations may be built on top of it, such as Min or Max -

static int? Min(IEnumerable<int> values)
{
  return values.Aggregate(
    seed: (int?)null,
    func: (valueSoFar, nextValue) => (valueSoFar.HasValue && valueSoFar < nextValue)
      ? valueSoFar
      : nextValue
  );
}

static int? Max(IEnumerable<int> values)
{
  return values.Aggregate(
    seed: (int?)null,
    func: (valueSoFar, nextValue) => (valueSoFar.HasValue && valueSoFar > nextValue)
      ? valueSoFar
      : nextValue
  );
}

To functional code.. one step at a time

Back to the Single Layer Perceptron code.. The way that I'm approaching this is to take one logical section of code and replace the procedural style of code with functional constructs.

The first that I'll tackle is the do..while loop and the mutation of the outer "iteration", "weights", "bias" and "globalError" variables.

This will be straightforward if we use the Aggregate method where the "value so far" contains a "Weights" array, a "Bias" value and a "GlobalError" value that will be re-calculated each iteration.

The input list passed to Aggregate will be an incrementing list of integers representing the current iteration number. The "func" lambda will take the previous Weights / Bias / GlobalError state and calculate the next Weight / Bias / GlobalError state. If the "previousState" already has a low enough GlobalError then the "func" lambda won't have to do any more calculating and can just return the previousState reference immediately (meaning that we don't have to do any more work and we can just let Aggregate finish as many iterations as it is configured to do so until the Aggregate call completes - if that sounds a bit unclear then hopefully it will make more sense after you see the code and I talk more about it below).

const double learningRate = 0.1;
const int maxNumberOfIterationsToPerform = 100; // See notes below code

var finalResult = Enumerable.Range(0, maxNumberOfIterationsToPerform)
  .Aggregate(
    seed: new
    {
      Weights = new[] { r.NextDouble(), r.NextDouble() },
      Bias = 0d,
      GlobalError = double.MaxValue
    },
    func: (previousState, iteration) =>
    {
      // The network is already trained - no more calculations required
      if (previousState.GlobalError == 0)
        return previousState;

      var weights = previousState.Weights;
      var bias = previousState.Bias;
      var globalError = 0d;
      for (var p = 0; p < trainingData.Length; p++)
      {
        // Calculate output
        var inputs = trainingData[p].Item1;
        var output = Output(weights, bias, inputs[0], inputs[1]) ? 1 : -1;

        // Calculate error
        var expected = trainingData[p].Item2;
        var localError = (expected ? 1 : -1) - output;
        if (localError != 0)
        {
          // Update weights (taking a copy of the weights array rather than altering its values)
          weights = weights.ToArray();
          for (var i = 0; i < 2; i++)
          {
            weights[i] += learningRate * localError * inputs[i];
          }
          bias += learningRate * localError;
        }

        // Convert error to absolute value
        globalError += Math.Abs(localError);
      }
      Console.WriteLine("Iteration {0}\tError {1}", iteration, globalError);
      return new { Weights = weights, Bias = bias, GlobalError = globalError };
    }
  );

(You may notice that I also changing "learningRate" from being a variable to be a const - since this will never change, it makes sense).

I've had to make a compromise in how I've written this code - I've had to specify a "maxNumberOfIterationsToPerform" value because the Aggregate method has no way to say "stop processing now, we have an answer that we're happy with". This is why there is the check at the top of the "func" lambda that says "if previousState's GlobalError is low enough then do no more calculation" - the Aggregate method will keep running through every single value in the input list. But how do we know that 100 iterations will be enough to get a zero Global Error? We don't!

What would be really helpful would be if we could have a variation of Aggregate that returns an IEnumerable of all of the intermediate calculation states (all of the "previousState" values) so that we could stop enumerating as soon as one of them has a GlobalError of zero - that way we wouldn't have to limit ourselves to a low maxNumberOfIterationsToPerform value. Something that would let us write code like this:

const double learningRate = 0.1;

var finalResult = Enumerable.Range(0, int.MaxValue)
  .AggregateAndReturnIntermediateStates(
    seed: new
    {
      // Same as in earlier code sample..
    },
    func: (previousState, iteration) =>
    {
      // Same as in earlier code sample but without the need to check GlobalError..
    }
  )
  .First(state => state.GlobalError == 0);

I searched through the LINQ and the F# library documentation and I couldn't find anything in LINQ that I could use to do this but I did find something in F# called "scan". To implement it as a LINQ-esque C# extension method, though, is simple. If we start by considering what an implementation of Aggregate would look like:

public static TAccumulate Aggregate<TSource, TAccumulate>(
  this IEnumerable<TSource> source,
  TAccumulate seed,
  Func<TAccumulate, TSource, TAccumulate> func)
{
  var valueSoFar = seed;
  foreach (var value in source)
    valueSoFar = func(valueSoFar, value);
  return valueSoFar;
}

.. we need only to change the return type from TAccumulate to IEnumerable<TAccumulate> and to throw in some "yield return" magic to produce "Scan":

public static IEnumerable<TAccumulate> Scan<TSource, TAccumulate>(
  this IEnumerable<TSource> source,
  TAccumulate seed,
  Func<TAccumulate, TSource, TAccumulate> func)
{
  yield return seed;

  var valueSoFar = seed;
  foreach (var value in source)
  {
    valueSoFar = func(valueSoFar, value);
    yield return valueSoFar;
  }
}

This means that I can now write:

const double learningRate = 0.1;

var finalResult = Enumerable.Range(0, int.MaxValue)
  .Scan(
    seed: new
    {
      // Same as in earlier code sample..
    },
    func: (previousState, iteration) =>
    {
      // Same as in earlier code sample (but still without the need to check GlobalError)..
    }
  )
  .First(state => state.GlobalError == 0);

Hurrah! That's a good step forward!

Now I need to tackle the inner section:

var weights = previousState.Weights;
var bias = previousState.Bias;
var globalError = 0d;
for (var p = 0; p < trainingData.Length; p++)
{
  // Calculate output
  var inputs = trainingData[p].Item1;
  var output = Output(weights, bias, inputs[0], inputs[1]) ? 1 : -1;

  // Calculate error
  var expected = trainingData[p].Item2;
  var localError = (expected ? 1 : -1) - output;
  if (localError != 0)
  {
    // Update weights (taking a copy of the weights array rather than altering its values)
    weights = weights.ToArray();
    for (var i = 0; i < 2; i++)
    {
      weights[i] += learningRate * localError * inputs[i];
    }
    bias += learningRate * localError;
  }

  // Convert error to absolute value
  globalError += Math.Abs(localError);
}

Console.WriteLine("Iteration {0}\tError {1}", iteration, globalError);
return new { Weights = weights, Bias = bias, GlobalError = globalError };

I'm going to start from the inside and work outward this time. The first thing that I want to get rid of is the loop that is used to update weights. What this loop is effectively doing is walking through two arrays ("weights" and "inputs") and performing an operation on a single pair of items from each (each loop iteration, we do something with one weight value and one input value).

This is just what the "Zip" LINQ function does and so we can use that here. We'll replace:

// Update weights (taking a copy of the weights array rather than altering its values)
weights = weights.ToArray();
for (var i = 0; i < 2; i++)
{
  weights[i] += learningRate * localError * inputs[i];
}

.. with this:

weights
  .Zip(inputs, (weight, input) => weight + (learningRate * localError * input))
  .ToArray();

To maker the "inner section" simpler, I'm going to hide that logic into a function:

private static double[] UpdateWeights(double[] weights, double learningRate, double localError, double[] inputs)
{
  if (localError == 0)
    return weights;

  return weights
    .Zip(inputs, (weight, input) => weight + (learningRate * localError * input))
    .ToArray();
}

I've also pulled the "is localError zero" check into the method. It feels a little unnecessary when there are only two weights and two inputs but this new version of the weight-updating code may be called with any number of inputs and so it may make sense to avoid looping through them all when the localError is zero (because we won't be making any changes to the weights in that case).

The next thing to do is to get rid of the other for-loop and the values that it mutates on each iteration. This part:

var weights = previousState.Weights;
var bias = previousState.Bias;
var globalError = 0d;
for (var p = 0; p < trainingData.Length; p++)
{
  // Apply current pattern and alter weights, bias and globalError accordingly..
}

If we group the "weights / bias / globalError" values into a single value then we can replace this with an Aggregate call, like we saw earlier:

var resultForIteration = trainingData.Aggregate(
  seed: new { Weights = previousState.Weights, Bias = previousState.Bias, GlobalError = 0d },
  func: (stateSoFar, pattern) =>
  {
    // Apply current pattern and calculate new weights, bias and globalError values..

    // .. and return new object wrapping these values
    return new { Weights = newWeights, Bias = newBias, GlobalError = newGlobalError },
  }
);

Before I pull it all together, I want to make a small change to the "Output" function - the current version only works if there are precisely two inputs and two weights but the "UpdateWeights" function from a moment ago works with any number of inputs and so I think that "Output" should too. So we'll replace this:

private static bool Output(double[] weights, double bias, double x, double y)
{
  var sum = (x * weights[0]) + (y * weights[1]) + bias;
  return (sum >= 0);
}

.. with this:

private static bool Output(double[] weights, double bias, double[] inputs)
{
  var sum = inputs.Zip(weights, (input, weight) => input * weight).Sum() + bias;
  return (sum >= 0);
}

(Note that using "Zip" again means that we don't have to resort to any for loops)

Combining all of this, the network-training code becomes the following:

const double learningRate = 0.1;

var finalResult = Enumerable.Range(0, int.MaxValue)
  .Scan(
    seed: new
    {
      Weights = new[] { r.NextDouble(), r.NextDouble() },
      Bias = 0d,
      GlobalError = double.MaxValue
    },
    func: (previousState, iteration) =>
    {
      var resultForIteration = trainingData.Aggregate(
        seed: new { Weights = previousState.Weights, Bias = previousState.Bias, GlobalError = 0d },
        func: (stateSoFar, pattern) =>
        {
          var output = Output(stateSoFar.Weights, stateSoFar.Bias, pattern.Item1) ? 1 : -1;
          var localError = (pattern.Item2 ? 1 : -1) - output;
          return new
          {
            Weights = UpdateWeights(stateSoFar.Weights, learningRate, localError, pattern.Item1),
            Bias = stateSoFar.Bias + (learningRate * localError),
            GlobalError = stateSoFar.GlobalError + Math.Abs(localError)
          };
        }
      );
      Console.WriteLine("Iteration {0}\tError {1}", iteration, resultForIteration.GlobalError);
      return resultForIteration;
    }
  )
  .First(state => state.GlobalError <= 0);

The final piece of the puzzle is to change the "Display network generalisation" code to remove the for loops from there too -

for (double x = 0; x <= 1; x += .25)
{
  for (double y = 0; y <= 1; y += .25)
  {
    var output = Output(weights, bias, new[] { x, y });
    Console.WriteLine("{0},\t{1},\t{2}", x, y, output ? "Yes" : "No");
  }
}

The natural thing would seem to be to replace those loops with Enumerable.Range calls.. however, "Range" only works int values and we need to use double in order to increment by 0.25 each time. We could write a new "Range" extension method that would take double values or we could just workaround the limitation. If we want the values 0, 0.25, 0.5, 0.75, 1 then that's five distinct values. The number of items may be calculated by taking the end value, subtracting the start value, dividing by the increment and then adding one (to ensure that we get the start value and the end value).

In this case, that would be ((1 - 0) / 0.25) + 1 = 4 + 1 = 5.

We can do that in code like this:

const double startAt = 0;
const double endAt = 1;
const double increment = 0.25;
var range = Enumerable.Range(0, (int)((endAt - startAt) / increment) + 1)
  .Select(value => value * increment);

We then want to "cross join" range with itself so that we loop through every (x, y) combination. We can do that with creative use of "SelectMany" -

var xyPairs = range.SelectMany(value => range, (x, y) => new[] { x, y });

And now that nested for-loop may be replaced by this:

const double startAt = 0;
const double endAt = 1;
const double increment = 0.25;
var range = Enumerable.Range(0, (int)((endAt - startAt) / increment) + 1)
  .Select(value => value * increment);
var xyPairs = range.SelectMany(value => range, (x, y) => new[] { x, y });
Console.WriteLine(string.Join(
  Environment.NewLine,
  xyPairs.Select(inputs => $"{string.Join("\t", inputs)}\t{(Output(finalResult.Weights, finalResult.Bias, inputs) ? "Yes" : "No")}")
));

That's the final piece of the convert-to-functional-code puzzle. Now we just need to translate it into F#!

Sidebar: "Function" vs "Method"

I find that in languages that are thought to be object oriented, the words "function" and "method" are commonly used interchangeably. Since beginning to become interested in so-called "functional programming", I've tried to find out whether there is a definitive or accepted difference between the two (after all, it's called functional programming rather than methodical programming, so surely someone thought that there was a difference!).

A few times, I've heard that the difference is that a "function" should not have any side effects and so should always return the same value given the same inputs. On the other hand, a "method" may cause side effects or rely upon ambient references - if the code writes to disk or reads DateTime.Now then it's not "pure" (where "pure" means that it relies only upon its arguments and does not produce any side effects - it only produces a return value and does not manipulate anything else) and so should be described as being part of a method rather than part of a function. Most recently I've seen it described in this Software Engineering Stack Exchange answer.

I try to use the word "function" only when it is known to be a pure function and a "method" otherwise (when it either definitely causes / relies upon side effects or if it's not clear). I still get it wrong from time to time (for example, I've been referring to LINQ "methods" in this post and we can probably presume that they are pure functions in most cases) but I'm still in the process of trying to internalise this terminology while I'm trying to internalise writing a more "functional" style of code for writing F#.

Writing F# code

If you've read this far then you may be detecting an unexpectedly abrupt end to the post judging by your browser's scrollbar!

Originally, I had intended to include all of the above content and go into how precisely to translate the functional C# code into F# but it quickly became clear that the post would be insanely large (I've written my fair share of monster posts in the past and I think that the time has come to put an end to them - this one's already pretty hefty).

Cliffhanger!

Sorry.

My next post will jump straight into F#. I will assume zero prior knowledge of the language itself but I also want to proceed at a decent rate. Hopefully this will mean that you won't get bored if you already have a little exposure to F# (or maybe it will be the worst of both worlds and be too slow for F# novices but too fast for those who've never seen it before). Let's wait and see*!

* (Should you be desperately excited and dying for part two, rest assured that it's already written and just needs a thorough proof-read - so it should be published early next week at the latest)

I'm not sure how many posts there will be in the series in total but the Single Layer Perceptron is just the first model that I want to cover before moving onto the Back Propagation Neural Network model and then onto the Multi-Output variation (which will be necessary in order to classify hand written digits from 0-9 as opposed to being a simple yes/no classifier). Although I said that performance is not my primary concern for this playing-with-F# process, there are a couple of interesting things that I'd like to talk about on that front. So there should be a lot to come over the next few months!

Posted at 22:18

Comments