So.. what is machine learning? (#NoCodeIntro)
TL;DR
Strap in, this is a long one. If the title of the post isn't enough of a summary for you but you think that this "TL;DR" is too long then this probably isn't the article for you!
A previous job I had was, in a nutshell, working on improving searching for files and documents by incorporating machine learning algorithms - eg. if I've found a PowerPoint presentation that I produced five years ago on my computer and I want to find the document that I made with loads of notes and research relating to it, how can I find it if I've forgotten the filename or where I stored it? This product could pull in data from many data sources (such as Google Docs, as well as files on my computer) and it could, amongst other things, use clever similarity algorithms to suggest which documents may be related to that presentation. This is just one example but even this is a bit of a mouthful! So when people outside of the industry asked me what I did, it was often hard to answer them in a way that satisfied us both.
This came to a head recently when I tried to explain to someone semi-technical what the difference actually was between machine learning and.. er, not machine learning. The "classic approach", I suppose you might call it. I tried hard but I made a real meal of the explanation and doing lots of hand waving did not make up for a lack of whiteboard, drawing apparatus or a generally clear manner to explain. So, for my own peace of mind (and so that I can share this with them!), I want to try to describe the difference at a high level and then talk about how machine learning can work (in this case, I'll mostly be talking about "supervised classification" - I'll explain what that means shortly and list some of the other types) in a way that is hopefully understandable without requiring any coding or mathematical knowledge.
The short version
- The "classic approach" involves the programmer writing very specific code for every single step in a given process
- "Supervised classification" involves the programmer writing some quite general (ie. not specific to the precise task) code and then giving it lots of information along with a brief summary of each piece of information (also known as a label) so that it can create a "trained model" that can guess how to label new information that it hasn't seen before
What this means in practice
An example of the first ("classic") approach might be to calculate the total for a list of purchases:
- The code will look through each item and lookup in a database what rate of tax should be applied to it (for example, books are exempt from VAT in the UK)
- If there is a tax to apply then the tax for the item will be calculated and this will be added to the initial item's cost
- All of these costs will be added up to produce a total
This sort of code is easy to understand and if there are any problems encountered in the process then it's easy to diagnose them. For example, if an item appeared on the list that wasn't in the database - and so it wasn't possible to determine whether it should be taxed or not - then the problem could easily stop with an "item not found in database" error. There are a lot of advantages to code being simple to comprehend and having it easy to understand how and why bad things have happened.
(Anyone involved in coding knows that dealing with "the happy path" of everything going to plan is only a small part of the job and it's often when things go wrong that life gets hard - and the easier it is to understand precisely what happened when something does go wrong, the better!)
An example of the second ("machine learning") approach might be to determine whether a given photo is of a cat or a dog:
- There will be non-specific (or "generic") code that is written that can take a list of "labelled" items (eg. this is a picture of a cat, this is a picture of a dog) and use it to predict an unseen and unlabelled item (eg. here is a picture - is it a cat or a dog?) - this code is considered to be generic because nothing in the way it is written relates to cats or dogs, all it is intended to do is be able to receive lots of labelled data and produce a trained model that can make predictions on future items
- The code will be given a lot of labelled data (maybe there are 10,000 pictures of cats and 10,000 pictures of dogs) and it will perform some sort of clever mathematics that allows it to build a model trained to differentiate between cats and dogs - generally, the more labelled data that is provided, the better the final trained model will be at making predictions.. but the more data that there is, the longer that it will take to train
- When it is finished "training" (ie. producing this "trained model"), it will then be able to be given a picture of a cat or a dog and say how likely it is that it thinks it is a cat vs a dog
This sounds like quite a silly example but there are many applications of this sort of approach that are really useful - for example, the same non-specific/generic code could be given inputs that are scans of hospital patients where it is suspected that there is a cancerous growth in the image. It would be trained by being given 1,000s of images that doctors have already said "this looks like a malignant growth" or "this looks like nothing to worry about" and the trained model that would be produced from that information would then be able to take images of patient scans that it's never seen before and predict whether it shows something to worry about.
(This sort of thing would almost certainly never replace doctors but it could be used to streamline some medical processes - maybe the trained model is good enough that if it predicts with more than 90% certainty that the scan is clear then a doctor wouldn't need to look at it but if there was even a 10% chance that it could be a dangerous growth then a doctor should look at it with higher priority)
Other examples could be taken from self-driving cars; from the images coming from the cameras on the car, does it look like any of them indicate pedestrians nearby? Does it look like there are speed limit signs that affect how quickly the car may travel?
The results of the trained model need not be binary (only two options), either - ie. "is this a picture of a cat or is it a picture of a dog?". It could be trained to predict a wide range of different animals, if we're continuing on the animal-recognition example. In fact, an application that I'm going to look at in more depth later is using machine learning to recognise hand-written digits (ie. numbers 0 through 9) because, while this is a very common introductory task into the world of machine learning, it's a sufficiently complicated task that it would be difficult to imagine how you might solve it using the "classic" approach to coding.
Back to the definition of the type of machine learning that I want to concentrate on.. the reason it's referred to as "supervised classification" is two-fold:
- The trained model that it produces has the sole task of taking inputs (such as pictures in the examples above, although there are other forms of inputs that I'll mention soon) and predicting a "classification" for them. Generally, it will offer a "confidence score" for each of the classifications that it's aware of - to continue the cat/dog example, if the trained model was given a picture of a cat then it would hopefully give a high prediction score that it was a cat (generally presented as a percentage) and the less confident it was that it was a cat, the more confident it would be that the picture was of a dog.
- The model is trained by the "labelled data" - it can't guess which of the initial pictures are cats and which are dogs if it's just given a load of unlabelled pictures and no other information to work from. The fact that this data is labelled means that someone has had to go through the process of manually applying these labels. This is the "supervised" aspect.
There are machine learning algorithms (where an "algorithm" is just a set of steps and calculations performed to produce some result) that are described as "unsupervised classification" but the most common example of this would be to train a model on a load of inputs and ask it to split them into groups based upon which it thinks seem most similar. It won't be able to give a name to each group because all it has access to is the raw data of each item and no "label" for what each one represents.
This sort of approach is a little similar to how the "find related documents" technology that I described at the top of this post works - the algorithm looks for "features"* that it thinks makes it quite likely that two documents contain the same sort of content and uses this to produce a confidence score that they may be related. I'll talk about other types of machine learning briefly near the end of this post but, in an effort to give this any semblance of focus, I'm going to stick with talking about "supervised classification" for the large part.
* ("Features" has a specific meaning in terms of machine learning algorithms but I won't go into detail on it right now, though I will later - for now, in the case of similar documents, you can imagine "features" as being uncommon words or phrases that are more likely to crop up in documents that are similar in some manner than in documents that are talking about entirely different subject matters)
Supervised classification with neural networks
Right, now we're sounding all fancy and technical! A "neural network" is a model commonly used for supervised classification and I'm going to go through the steps of explaining how it is constructed and how it works. But first I'm going to try to explain what one is.
The concept of a neural net was inspired by the human brain and how it has neurons that connect to each other with varying strengths. The strengths of the connections are developed based upon patterns that we've come to recognise. The human brain is amazing at recognising patterns and that's why two Chicago researchers in 1944 were inspired to wonder if a similar structure could be used for some form of automated pattern recognition. I'm being intentionally vague here because the details aren't too important and the way that connections are made in the human brain is much more complicated than those in the neural networks that I'll be talking about here, so I only really mention it for a little historical context and to explain some of the names of things.
A neural net has a set of "input neurons" and a set of "output neurons", where the input neurons are connected to the output neurons.
Each time that the network is given a single "input" (such as an image of a cat), that input needs to be broken down into values to feed to the input neurons; these input neurons accept numeric values between 0 and 1 (inclusive of those two values) and it may not immediately be apparent how a picture can be somehow represented by a list of 0-to-1 values but I'll get to that later.
There are broadly two types of classifier and this determines how many output neurons there will be - there are "binary classifiers" (is the answer yes or no; eg. "does this look like a malignant growth or not?") and there are "multi-class classifier" (such as a classifier that tries to guess what kind of fruit an image is of; a banana, an apple, a mango, an orange, etc..). A binary classifier will have one output neuron whose output is a confidence score for the yes/no classification (eg. it is 10% certain that it is not an indication of cancer) while a multi-class classifier will have as many output neurons as there are known outputs (so an image of a mango will hopefully produce a high confidence score for the mango output neuron and a lower confidence score for the output neurons relating to the other types of fruit that it is trained to recognise).
Each connection from the input neurons to the output neurons has a "weight" - a number that represents how strong the connection is. When an "input pattern" (which is the name for the list of 0-to-1 input neuron values that a single input, such as a picture of a cat, maybe represented by) is applied to the input neurons, the output neurons are set to a value that is the sum of every input neuron's value that is connected to it multiplied by the weight of the connection.
I know that this is sounding very abstract, so let's visualise some extremely simple possible neural nets.
Examples that are silly to use machine learning for but which are informative for illustrating the principles
The image below depicts a binary classifier (because there is only one output neuron) where there are only two input neurons. The connections between the two inputs neurons to the single output neuron each have a weight of 0.3.
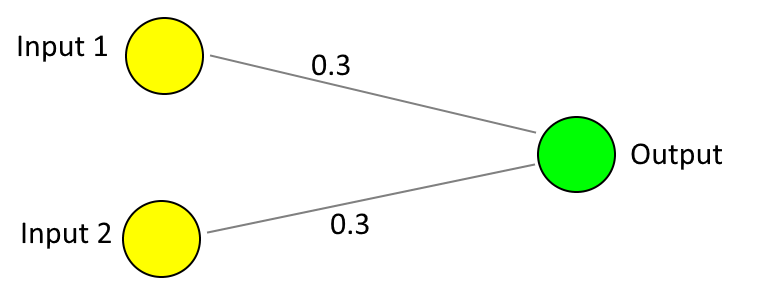
This could be considered to be a trained model for performing a boolean "AND" operation.. if you'll allow me a few liberties that I will take back and address properly shortly.
An "AND" operation could be described as a light bulb that is connected to two switches and the light bulb only illuminates if both of the switches are set to on. If both switches are off then the light bulb is off, if only one of the switches is on (and the other is off) then the light bulb is off, if both switches are on then the light bulb turns on.
Since the neuron inputs have to accept values between 0 and 1 then we could consider an "off" switch as being a 0 input and an "on" switch as being a 1 input.
If both switches are off then the value at the output is (0 x 0.3) + (0 x 0.3) = 0 because we take the input values, multiply them by their connection weights to the output and add these values up.
If one switch is on and the other is off then the output is either (1 x 0.3) + (0 x 0.3) or (0 x 0.3) + (1 x 0.3), both of which equal 0.3 and we'll consider 0.5 to be the cut-off point at which we consider the output to be "on".
If both switches are on then the output is (1 x 0.3) + (1 x 0.3) = 0.6, which is greater than 0.5 and so we consider the output to be on, which is the result that we wanted!
Just in case it's not obvious, this is not a good use case for machine learning - this is an extremely simple process that would be written much more obviously in the "classic approach" to programming.
Not only would it be simpler to use the classic approach, but this is also not suited for machine learning because we know all of the possible input states and what their outputs should be - we know what happens when both switches are off and when precisely one switch is on and when both switches are on. The amazing thing with machine learning is that we can produce a trained model that can then make predictions about data that we've never seen before! Unlike this two-switches situation, we can't possibly examine every single picture of either a cat or a dog in the entire world but we can train a model to learn from one big set of pictures and then perform the crucial task of cat/dog identification in the future for photos that haven't even been taken yet!
For a little longer, though, I'm going to stick with some super-simple boolean operation examples because we can learn some important concepts.
Where the "AND" operation requires both inputs to be "on" for the output to be "on", there is an "OR" operation where the output will be "on" if either or both of the inputs are on. The weights on the network shown above will not work for this.
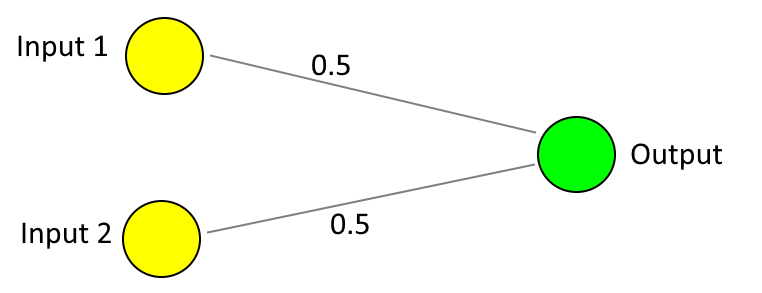
Now this second network would work to imitate an OR operation - if both switches are off then the output is (0 x 0.5) + (0 x 0.5) = 0, if precisely one switch is on then the output is (1 x 0.5) + (0 x 0.5) or (0 x 0.5) + (1 x 0.5) = 0.5, if both switches are on then the output is (1 x 0.5) + (1 x 0.5) = 1. So if both switches are off then the output is 0, which means the light bulb should be off, but if one or both of the switches are on then the output is at least 0.5, which means that the light bulb should be on.
This highlights that the input neurons and output neurons determine the form of the data that the model can receive and what sort of output/prediction it can make - but it is the weight of the connections that control what processing occurs and how the input values contribute in producing produce the output value.
- *(Note that there can be more layers of neurons in between the input and output layer, which we'll see an example of shortly)
In both of the two examples above, it was as if we were looking at already-trained models for the AND and the OR operations but how did they get in that state? Obviously, for the purposes of this post, I made up the values to make the examples work - but that's not going to work in the real world with more complex problems where I can't just pull the numbers out of my head; what we want is for the computer to determine these connection weight values and it does this by a process of trial and improvement and it is this act that is the actual "machine learning"!
The way that it often works is that, as someone who wants to train a model, I decide on the number of inputs and outputs that are appropriate to my task and then the computer has a representation of a neural network of that shape in its memory where it initially sets all of the connection weights to random values. I then give it my labelled data (which, again, is a list of inputs and the expected output - where each individual "input" is really a list of input values that are all 0-1) and it tries running each of those inputs through its neural network and compares the calculated outputs to the outputs that I've told it to expect. Since this first attempt will be using random connection weights, the chances are that a lot of its calculated output will not match the outputs that I've told it to expect. It will then try to adjust the connection weights so that hopefully things get a bit closer and then it will try running all of the inputs through the neural network with the new weights and see if the calculated outputs are closer to the expected output. It will do this over and over again, making small adjustments to the connection weights each time until it produces a network with connection weights that calculate the expected output for every input that I gave it to learn with.
The reason that the weights that it uses initially are random values (generally between 0 and 1) is that the connection weight values can actually be any number that makes the network operate properly. While the input values are all 0-1 and the output value should end up being 0-1, the connection weights could be larger than one or they could be negative; they could be anything! So your first instinct might be "why set them all to random values instead of setting them all to 0.5 initially" and the answer is that while 0.5 is the mid-point in the allowable ranges for the input values and the output values, there is no set mid-point for the connection weight values. You may then wonder why not set them all to zero because that sounds like it's in the middle of "all possible numbers" (since the weights could be positive or they could be negative) and the machine learning could then either change them from zero to positive or negative as seems appropriate.. well, at the risk of skimming over details, numbers often behave a little strangely in some kinds of maths when zeroes are involved and so you generally get better results starting with random connection weight values, rather than starting with them all at zero.
Let's imagine, then, that we decided that we wanted to train a neural network to perform the "OR" operation. We know that there are two inputs required and one output. And we then let the computer represent this model in memory and have it give the connections random weight values. Let's say that it picks weights 0.9 and 0.1 for the connections from Input1-to-Output and Input2-to-Output, respectively.
We know that the labelled data that we're training with looks like this:
| Input 1 | Input 2 | Output |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
.. and the first time that we tried running these inputs through our 0.9 / 0.1 connection weight neural network, we'd get these results:
| Input 1 | Input 2 | Calculated Output | Expected Output | Is Correct |
|---|---|---|---|---|
| 0 | 0 | (0x0.9) + (0x0.1) = 0.0 | 0 | Yes (0.0 < 0.5 so consider this 0) |
| 0 | 1 | (0x0.9) + (1x0.1) = 0.1 | 1 | No (0.1 < 0.5 so consider this 0 but we wanted 1) |
| 1 | 0 | (1x0.9) + (0x0.1) = 0.9 | 1 | Yes (0.9 >= 0.5 so consider this 1) |
| 1 | 1 | (1x0.9) + (1x0.1) = 1.0 | 1 | Yes (1.9 >= 0.5 so consider this 1) |
Unsurprisingly (since completely random connection weights were selected), the results are not correct and so some work is required to adjust the weight values to try to improve things.
I'm going to grossly simplify what really happens at this point but it should be close enough to illustrate the point. The process tries to improve the model by repeatedly running every input pattern through the model (the input patterns in this case are (0, 0), (0, 1), (1, 0), (1, 1)) and comparing the output of the model to the output that is expected for each input pattern (as we know (0, 0) should have an output of < 0.5, while any of the input patterns (0, 1), (1, 0) and (1, 1) should have an output of >= 0.5). When there is a discrepancy in the model's output and the expected output, it will adjust one or more of the connection weights up and down.. then it will do it again and hopefully find that the calculated outputs are closer to the expected outputs, then again and again until the model's calculated outputs for every input pattern match the expected outputs.
So it will first try the pattern (0, 0) and the output will be 0 and so no change is needed there.
Then it will try (0, 1) and find that the output is too low and so it will increase the weight of the connections slightly, so now maybe they go from 0.9 / 0.1 to 0.91 / 0.11.
Then it will try (1, 0) with the new 0.91 / 0.11 weights and find that it gets the correct output (more than 0.5) and so make no change.
Then it will try (1, 1) with the same increased 0.91 / 0.11 weights and find that it still gets the correct output there and so make no more changes.
After this adjustment, the input pattern (0, 1) will still be too low (0 x 0.9) + (1 x 0.11) and so it will have to go round again.
It might continue doing this multiple times until the weights end up something like 0.5 / 1.4 and now it will have a model that gets all of the right values!
| Input 1 | Input 2 | Calculated Output | Expected Output | Is Correct |
|---|---|---|---|---|
| 0 | 0 | (0x1.4) + (0x0.5) = 0.0 | 0 | Yes (0.0 < 0.5 so consider this 0) |
| 0 | 1 | (0x1.4) + (1x0.5) = 0.5 | 1 | Yes (0.5 >= 0.5 so consider this 1) |
| 1 | 0 | (1x1.4) + (0x0.5) = 1.4 | 1 | Yes (1.4 >= 0.5 so consider this 1) |
| 1 | 1 | (1x1.4) + (1x0.5) = 1.9 | 1 | Yes (1.9 >= 0.5 so consider this 1) |
That's the very high-level gist, that it goes round and round in trying each input pattern and comparing the computed output to the expected output until the computed and expected outputs match. Great success!
(I'm not going to go into any more detail about how this weight-adjusting process works because I'm trying to avoid digging into any code in this post - just be aware that this process of calculating the output for each known input and then adjusting the connection weights and retrying until the output values are what we expect for each set of inputs is the actual training of the model, which I'll be referring to multiple times throughout the explanations here)
Now, there are a few things that may seem wrong based upon what I've said previously and how exactly it adjusts those weights through trial-and-improvement:
- The calculations here show that the four outputs are 0.0, 0.5, 1.4 and 1.9 but I said earlier that the input values should all be in the range 0-1 and the output values should be in the same range of 0-1
- Why does it adjust the weights so slowly when it needs to alter them; why would it only add 0.01 to the weight that connects Input1-to-Output each time?
Because I'm contrary, I'll address the second point first. If the weights were increased too quickly then the outputs may then "overshoot" the target output values that we're looking for and the next time that it tries to improve the values, it may find that it has to reduce them. Now, in this simple case where we're trying to model an "OR" operation, that's not going to be a problem because the input pattern (0, 0) will always get an output of 0 since it is calculated as (0 x Input1-to-Output-connection-weight) + (0 x Input2-to-Output-connection-weight) and that will always be 0, while the other three input patterns should all end up with an output of 0.5 or greater. However, for more complicated models, there will be times when weights need to be reduced in some cases as well as increased. If the changes made to the weights are too large then they might bounce back and forth on each attempt and ever settle into the correct values, so smaller adjustments are more likely to result in training a model that matches the requirements but at the cost of having to go round and round on the trial-and-improvement attempts more often.
This means that it will take longer to come to the final result and this is one of the issues with machine learning - for more complicated models, there can be a huge number of these trial-and-improvement attempts and each attempt has to run every input pattern through the model. When I was talking about training a model with 10,000 pictures of cats and 10,000 pictures of dogs and all these inputs have to be fed through a neural network until the outputs are correct then it can take a long time. That's not the case here (where there are only 4 input patterns and it's a very simple network) but for larger cases, there can be a point where you allow the model to train for a certain period and then accept that it won't be perfect but hope that it's good enough for your purposes, as a compromise against how long it takes to train - it can take days to train some really complex models with lots and lots of labelled data! Likewise, another challenge/compromise is trying to decide how quickly the weights should be adjusted - the larger the changes that it makes to the weight values of connections between neurons, the closer that it can get to a good result but it might actually make it impossible to get the best possible result if it keeps bouncing some of the weights back and forth, as I just explained!
Now to address the first point. There's a modicum of maths involved here but you don't have to understand it in any great depth. I've been pretending that the way to calculate the output value on our network is to take (Input1's value x the Input1-to-Output's connection weight) + (Input2's value x the Input2-to-Output's connection weight) but, as we've just seen, this result of this can be greater than 1 and input values and output values are all supposed to be within the 0-1 range. In fact, using this calculation, it would be possible to get a negative output value because neuron connection weights can be negative (I'll explain why in some more examples of machine learning a little later on) and that would also mean that the output value would fall outside of the 0-1 range that we require.
To fix this, we take the simple calculation that I've been using so far and pass the value through a formula that can take any number and squash it into the 0-1 range. While there are different formula options for neural networks, a common one is the "sigmoid function" and it would look like this if it was drawn on a graph (picture courtesy of Wikipedia) -
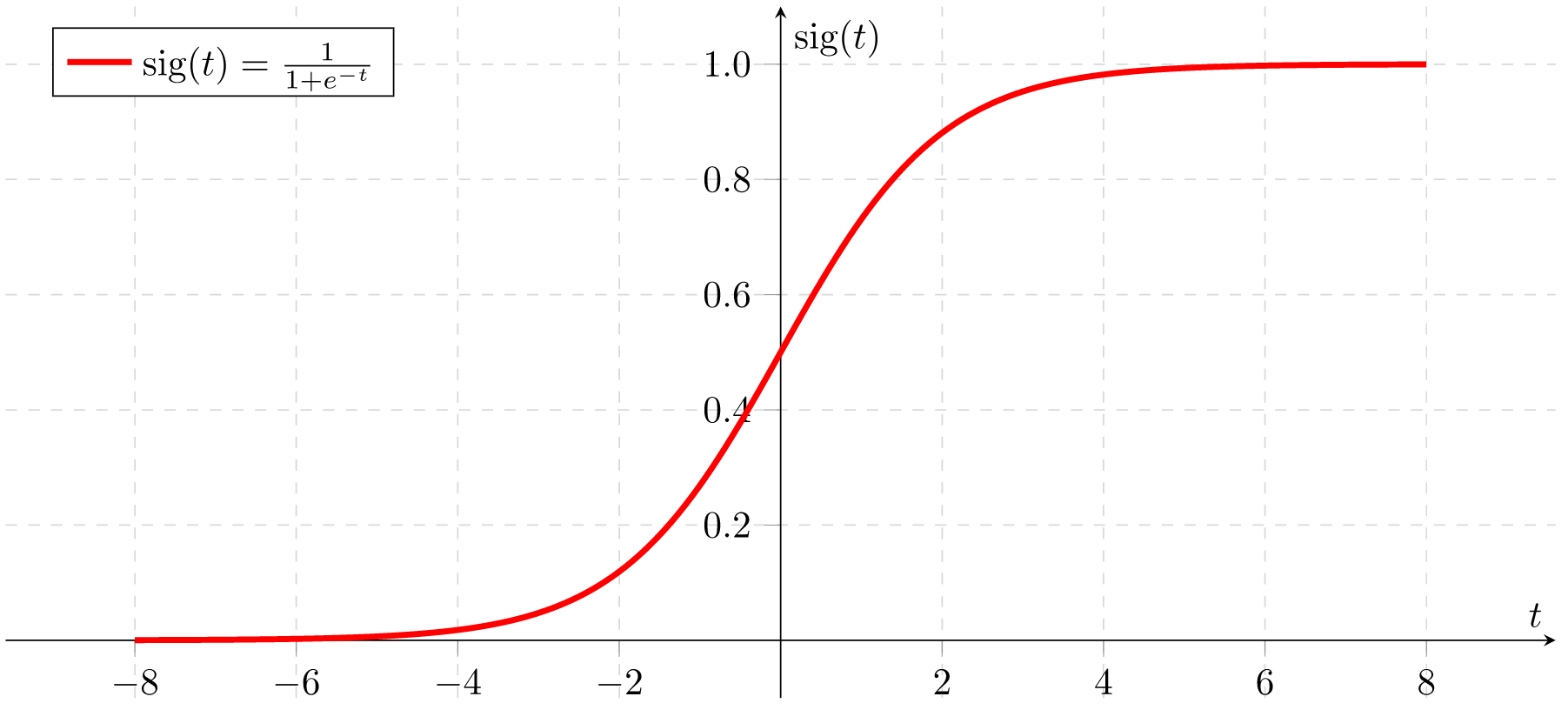
Although this graph only shows values from -8 to +8, you can see that its "S shape" means that the lines get very flat the larger that the number is. So if the formula is given a value of 0 then the result will be 0.5, if it's given a value of 2 then the result will be about 0.88, if it's given a value of 4 then the result is about 0.98, it's given a value of 8 then it's over 0.999 and the larger the value that the function is given the closer that the result will be to 1. It has the same effect for negative numbers - negative numbers that are -8 or larger (-12, -100, -1000) will all return a value very close to 0.
The actual formula for this graph is shown on the top left of the image ("sig(t) = 1 / (1 + e^-t)") but that's really not important to us right now, what is important is the shape of the graph and how it constrains all possible values to the range 0-1.
If we took the network that we talked about above (that trains a model to perform an "OR" operation and where we ended up with connection weights of 1.4 and 0.5) and then applied the sigmoid function to the calculated output values then we'd find that those weights wouldn't actually work and the machine learning process would have to produce slightly different weights to get the correct results. But I'm not going to worry about that now since the point of that example was simply to offer a very approximate overview of how the trial-and-improvement process works. Besides, we've got a more pressing issue to talk about..
The limits of such a simple network and the concept of "linearly separable" data
The two examples of models that we've trained so far are extremely simple in one important way - if you drew a graph with the four input values on them and were asked to draw a straight line that separated the inputs that should relate to an "off" state from the inputs that should relate to an "on" state then you do it very easily, like this:
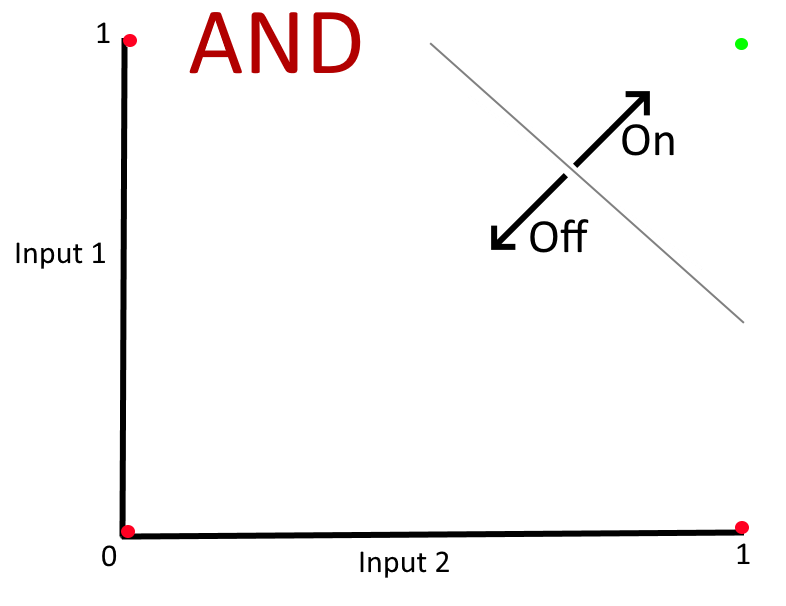
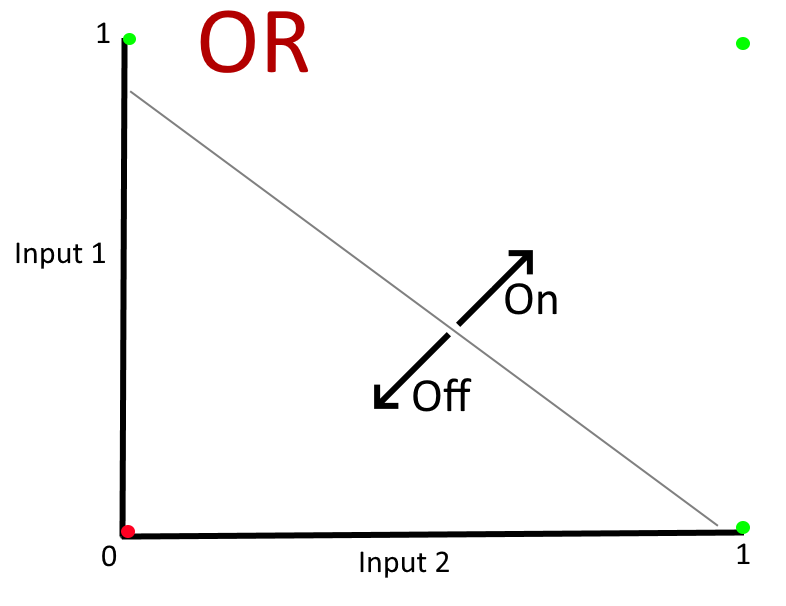
But not all sets of data can be segregated so simply and, unfortunately, it is a limitation to the very simple network shape that we've seen so far (where the input layer is directly connected to the output layer) that it can only work if the data can be split with all positive results on one side of a straight line and all negative results on the other side. Cases where this is possible (such as the "AND" and "OR" examples) are referred to as being "linearly separable" (quite literally, the results in either category can be separated by a single straight line and the model training is, in effect, to work out where that line should lie). Interestingly, there are actually quite a lot of types of data analysis that have binary outcomes that are linearly separable - but I don't want to go too far into talking about that and listing examples because I can't cover everything about machine learning and automated data analysis in this post!
A really simple example of data that is not linearly separable is an "XOR" operation. While I imagine that the "AND" and "OR" operations are named so simply that you could intuit their definitions without a grounding in boolean logic, this may require slightly more explanation. "XOR" is an abbreviation of "eXclusive OR" and, to return to our light bulb and two switches example, the light should be off if both switches are off, it should be on if one of the switches is on but it should be off if both of the switches are on. On the surface, this sounds like a bizarre situation but it's actually encountered in nearly every two-storey residence in the modern world - when you have a light on your upstairs landing, there will be a switch for it downstairs and one upstairs. When both switches are off, the light is off. If you are downstairs and switch the downstairs switch on then the light comes on. If you then go upstairs and turn on your bedroom light, you may then switch the upstairs landing light and the light will go off. At this point, both switches are on but the light is off. So the upstairs light is only illuminated if only one of the switches is on - when they're both on, the light goes off.
If we illustrated this with a graph like the "AND" and "OR" graphs above then you can see that there is no way to draw a single straight line on that graph where every state on one side of the line represents the light being on while every state on the other side of the line represents the light being off.
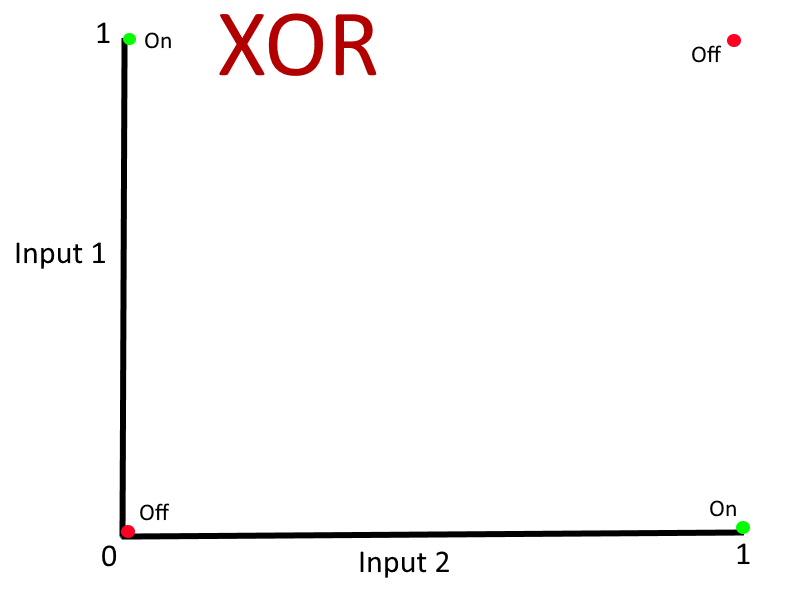
This is a case where the data points (where "data" means "all of the input patterns and their corresponding output values") are not linearly separable. And this means that the simple neural network arrangement that we've seen so far can not produce a trained model that can represent the data. If we tried to train a model in the same way as for AND and OR, the neuron connection weights would go back and forth as the training process kept finding that its "trial-and-improvement" approach continuously came up with at least one wrong result.
There is a solution to this, and that is to introduce another layer of neurons into the graph. In our simple network, there are two "layers" of neurons - the "input" neurons on the left and the "output" neuron on the right. What we would need to do here is add a layer in between, which is referred to as a "hidden layer". A neural network to do this would look something like the following:
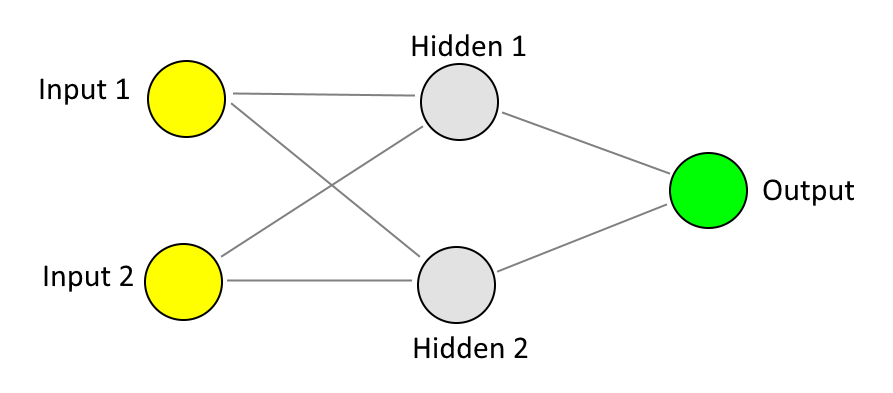
To calculate the output value for any pair of input values, more calculations are required now that we have a hidden layer. Whereas before, we only had to multiple Input 1 by the weight that joined it to the Output and add that value to Input 2 multiplied by its connection we weight, now we have three hidden layer neurons and we have to:
- Multiply Input 1's value by the weight of its connection to Hidden Input 1 and then add that to Input 2's value multiplied by its connection weight to Hidden Input 1 to find Hidden Input 1's "initial value"
- Do the same for Input 1 and Input 2 as they connect to Hidden Input 2
- Apply the sigmoid function for each of the Hidden Input values to ensure that they are between 0 and 1
- Take Hidden Input 1's value multiplied by its connection weight to the output and add that to Hidden Input 2's value multiplied by its connection weight to the Output to find the Output's "initial value"
- Apply the sigmoid function to the Output value
The principle is just the same as when there were only two layers (the Input and Output), except now there are three and we have to take the Input layer and calculate values for the second layer (the Hidden layer) and then use the values there to calculate the value for third and final layer (the Output layer).
(Note that with this extra layer in the model, it is necessary to apply the sigmoid function after each calculation - we could get away with pretending that it didn't exist on the earlier examples but things would fall apart here if kept trying to ignore it)
The learning process described earlier can be applied here to determine what connection weights to use; start with all connection weights set to random values, calculate the final output for every set of inputs, then adjust the connection weights to try to get closer and repeat until the desired results are achieved.
For example, the learning process may result in the following weights being determined as appropriate:
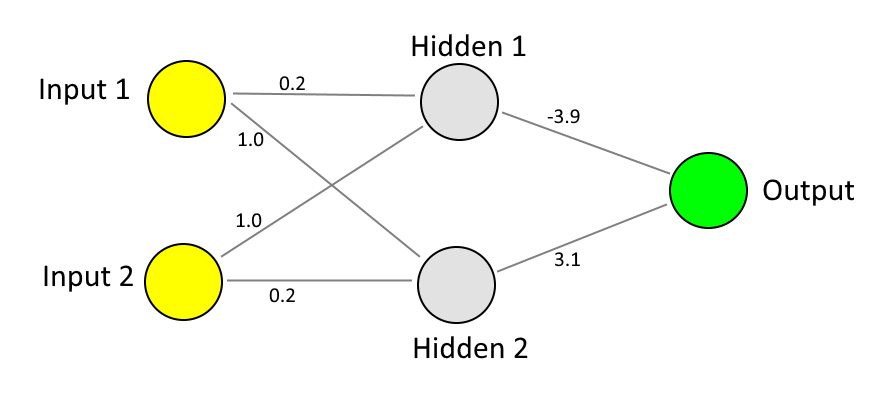
.. which would result in the following calculations occurring for the four sets of inputs (0, 0), (1, 0), (0, 1) and (1, 1) -
| Input 1 | Input 2 | Hidden 1 Initial | Hidden 2 Initial | Hidden 1 Sigmoid | Hidden 2 Sigmoid | Output Initial | Output Sigmoid |
|---|---|---|---|---|---|---|---|
| 0 | 0 | (0x0.2) + (0x0.2) = 0.0 |
(0x1) + (0x1) = 0.0 |
0.50 | 0.50 | (-3.9x0.50) + (3.1x0.50) = -0.40 |
0.17 |
| 0 | 1 | (0x0.2) + (1x0.2) = 0.2 |
(0x1) + (0x1) = 1.0 |
0.69 | 0.98 | (-3.9x0.69) + (3.1x0.98) = 0.35 |
0.80 |
| 1 | 0 | (1x0.2) + (0x0.2) = 0.2 |
(0x1) + (0x1) = 1.0 |
0.69 | 0.98 | (-3.9x0.69) + (3.1x0.98) = 0.35 |
0.80 |
| 1 | 1 | (1x0.2) + (1x0.2) = 0.4 |
(0x1) + (0x1) = 2.0 |
0.83 | 1.00 | (-3.9x0.83) + (3.1x1.00) = -0.14 |
0.36 |
Since we're considering an output greater than or equal to 0.5 to be equivalent to 1 and an output less than 0.5 to be equivalent to 0, we can see that these weights have given us the outputs that we want:
| Input 1 | Input 2 | Calculated Output | Expected Output | Is Correct |
|---|---|---|---|---|
| 0 | 0 | 0.17 | 0 | Yes (0.17 < 0.5 so consider this 0) |
| 0 | 1 | 0.80 | 1 | Yes (0.80 >= 0.5 so consider this 1) |
| 1 | 0 | 0.80 | 1 | Yes (1.80 >= 0.5 so consider this 1) |
| 1 | 1 | 0.36 | 0 | Yes (0.36 < 0.5 so consider this 0) |
How do you know if your data is linearly separable?
Or, to put the question another way, how many layers should your model have??
A somewhat flippant response would be that if you try to specify a model that doesn't have a hidden input layer and the training never stops calculating because it can find weights that perfectly match the data then it's not linearly separable. While it was easy to see with the AND and OR examples above that a training approach of fiddling with the connection weights between the two input nodes and the output should result in values for the model that calculate the outputs correctly, if we tried to train a model of the same shape (two inputs, one output, no hidden layers) for the XOR case then it would be impossible for the computer to find a combination of weights that would correctly calculate outputs for all of the possible inputs. You could claim that because the training process for the XOR case could never finish that it must not be linearly separable - and this is, sort of, technically, correct. But it's not very useful.
One reason that it's not very useful is that the AND, OR, XOR examples only exist to illustrate how neural networks can be arranged, how they can be trained and how outputs are calculated from the inputs. In the real world, it would be crazy to use a neural network for a tiny amount of fixed data for which all of the outputs are known - where a neural network becomes useful is when you use past data to predict future results. An example that I've used before is a fictitious history of a manager's decisions for feature requests that a team receives:
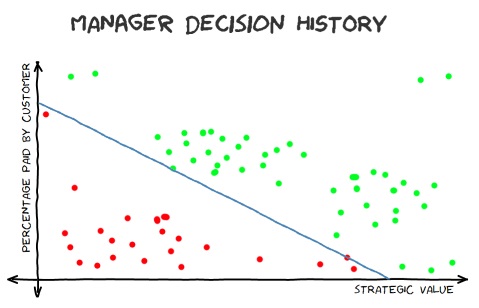
The premise is that every time this manager decides whether to give the green light or not to a feature that has been requested, they consider what strategic importance it has to the company and how much of the work the customer that is requesting it is willing to pay. If it's of high strategic importance and the customer expects to receive such value from it that they are willing to pay 100% of the costs of implementation then surely this manager will be delighted to schedule it! If the customer's budget is less than what it will cost to implement but the feature has sufficiently high strategic value to the company (maybe it will be a feature that could then be sold to many other customers to almost zero cost to the company or maybe it is an opportunity to address an enormous chunk of technical debt) then it still may get the go-ahead! But if the strategic value is low and the customer doesn't have the budget to cover the entire cost of development then the chances are that it will be rejected.
This graph only shows a relatively small number of points and it is linearly separable. As such, the data points on the graph could be used to train a simple two-input (strategic value on a scale of 0-1 and percentage payable by the customer on a scale of 0-1) and single-output binary classifier (the output is whether the feature gets agreed or rejected) neural network. The hope would be that the data used to train it is indicative of how that manager reacts to incoming requests and so it should be possible to take future requests and predict whether that manager is likely to take them on.
However, neural networks are often intended to be used with huge data sets and whenever there is a large amount of data then there is almost always bound to be some outliers present - results that just seem a little out of keeping with those around them. If you were going to train a model like this with 100,000 previous decisions then you might be satisfied with a model that can correctly is 99.9% accurate, which would mean that out of every 100,00 decisions that it might get 100 of them wrong. If you were trying to train a neural network model using 100,000 sets of historical inputs and outputs then you might decide that the computer can stop its training process when the neuron connection weights that it calculates results in outputs being calculated that are correct in 99.9% of cases, rather than hoping that a success rate of 100% can be achieved. This will have the advantage of finishing slightly more quickly but there's always a chance that a couple of those historical input/output entries were written down wrong and, with them included, the data isn't linearly separable - but with them excluded, the data is linearly separable. And so there is a distinction that can be made between whether the entirety of the data is, strictly speaking, linearly separable and whether a simple model can be trained (without any hidden layers) that is a close enough approximation.
The next problem with that simple approach ("if you can't use your data to train a model without hidden layers then it's not linearly separable") is that it suggests that adding in hidden layers will automatically mean that a neural network can be trained with the provided data - which is definitely not correct. Say, for example, that someone believed that this manager would accept or reject feature requests based upon what day of the week it was and what colour tie they were wearing that day. This person could provide historical data for sets of inputs and output - they know that decisions are only made Monday-to-Friday, which so that works itself easily into a 0-1 scale for one input (0 = Monday, 0.2 = Tuesday, etc..) and they have noticed that there are only three colours of tie worn (so a similar numeric value can be associated with each colour). The issue is that there is no correlation between these two inputs and the output, so it's extremely unlikely that a computer would be able to train a simple two-input / one-output model but that does not mean that adding in hidden layers would fix the problem!
This conveniently brings us to the subject of "feature selection". As I touched on earlier, features are measurable aspects of whatever we are trying to make predictions for. The "strategic importance" and "percentage that the customer will pay" were features on the example data before. Feature selection is an important part of machine learning - if you don't capture the right information then it's unlikely that you'll be able to produce something that makes good predictions. When I said before that there could be results in the managerial decision history that don't fit a linearly separable model for these two features, maybe it's not because some of the data points were written down wrong; maybe it's because other factors were at play. Maybe this manager is taking into account other factors such as an agreement with a customer that they can't foot the bill for the entirety of the current feature but they will contribute significantly to another feature that is of high strategic importance to the company but only if this first feature is also completed.
Capturing another feature in the model (perhaps something that reflects how likely the current feature request is to bring in future valuable revenue) is a case of adding another input neuron. So far, we've only seen networks that have two inputs but that has only been the case because they're very easy to talk about and to illustrate as diagrams and to describe calculations for and to draw graphs for! If a third feature was added then all of the calculation processes are essentially the same (if there are three inputs and one output then the output value is calculated by adding together each of the three input values multiplied by their connection weights) and it would still be possible to visualise, it's just that it would be in 3D rather than being a 2D graph. Adding a fourth dimension would mean that it couldn't be easily visualised but the maths and the training process would be the same - and this holds for adding a fifth, sixth or hundredth dimension!
(Other examples of features for the manager decision data might include "team capacity" and "opportunity cost" - would we be sacrificing other, more valuable work if we agree to do this task - and "required timescale for the feature" - is the customer only able to pay for it if it's delivered in a certain time frame, after which they would not be willing to contribute? I'm sure that you wouldn't have to think very hard to conjure up features like this that could explain the results that appear to be "outliers" when only the original two proposed features were considered)
It may well be that adding further relevant features is what makes a data set linearly separable, whereas before - in absence of sufficient information - it wasn't. And, while it can be possible to train a neural network using hidden layers such that it can take all of your historical input/output data and calculate neuron connection weights that make the network appear to operate correctly, it may not actually be useful for making future predictions - where it takes inputs that it hasn't seen before and determines an output. If it can't do this, then it's not actually very useful! A model that is trained to match its historical data but that is poor at making future predictions is said to have been a victim of "overfitting". A way to avoid that is to split up the historical data into "training data" and "test data" as I'll explain in the next section*.
* (I'll also finish answering the question about how many layers you should use and how large they should be!)
A final note on feature selection: In general, gathering more features in your data is going to be better than having fewer. The weights between neurons in a network represent how important the input is that the weight is associated with - this means that inputs/features that make a larger difference to the final output are going to end up with a higher weight in the trained model than inputs/features that are of lower importance. As such, irrelevant features tend to get ignored and so there is little downside to the final trained model from including them - in fact, there will be many circumstances where you don't know beforehand which features are going to be the really important ones and so you may be preventing yourself from training a good model if you exclude data! The downside is that the more inputs that there are, the more calculations need to be performed for each iteration of the "see how good the network is with the current weights and then adjust them accordingly", which can add up quickly if the amount of historical data being used to train is large. But you may well be happier with a model that took a long time to train into a useful state than you would be with a model that was quick to train but which is terrible at making predictions!
A classic example: Reading handwritten numeric digits
An extremely well-known data set that is often used in introductions to machine learning is MNIST; the Modified National Institute of Standards and Technology database, which consists of a large number of 28x28 pixel images of handwritten digits and the number that each image is a picture of (making it a collection of "labelled data" as each entry contains input data, in the form of the image, and an output value, which is the number that the image is known to be of).
It may seem counterintuitive but those 28x28 pixels can be turned into a flat list of 784 numbers (28 x 28 = 784) and they may be used as inputs for a neural network. The main reason that I think that it may be counterintuitive is that by going from a square of pixels to a one-dimensional list of numbers, you might think that valuable information is being discarded in terms of the structure of the image; surely it's important which pixels are above which other pixels or which pixels are to the left of which other pixels? Well, it turns out that discarding this "spatial information" doesn't have a large impact on the results!
Each 28x28 pixel image is in greyscale and every pixel has a brightness value in the range 0-255, which can easily be scaled down to the range 0-1 by dividing each value by 255.
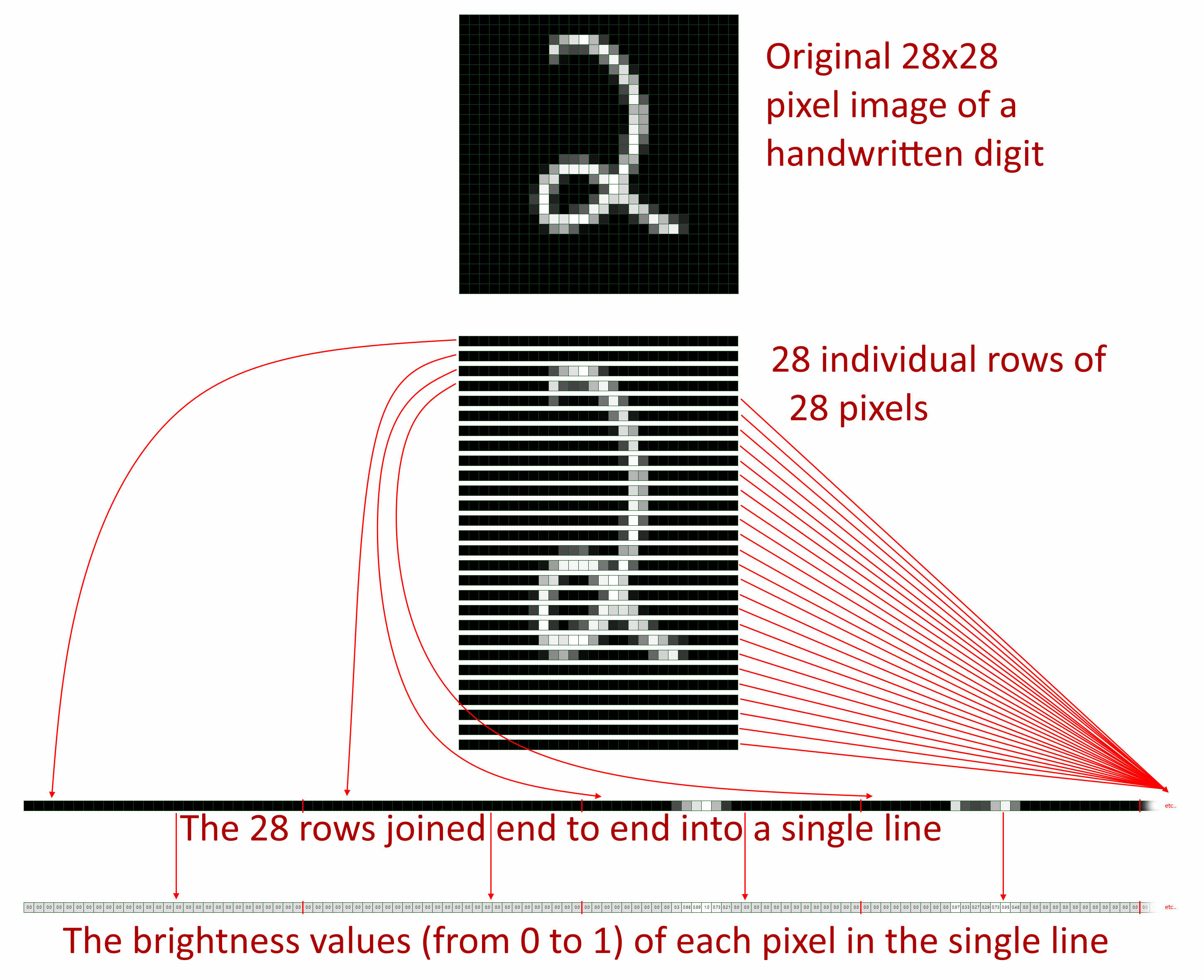
For the outputs, this is not a binary classifier (which is what we've looked at mostly so far); this is a multi-class classifier that has ten outputs because, for any given input image, it should predict whether the digit is 0, 1, etc.. up to 9.
The MNIST data (which is readily available for downloading from the internet) has two sets of data - the training data and the test data. Both sets of data are in the exact same format but the training data contains 60,000 labelled images while the test data contains 10,000 labelled images. The idea behind this split is that we can use the training data to train a model that can correctly give the correct output for each of its labelled images and then we confirm that the model is good by running the test data through it. The test data is the equivalent of "future data" that trained neural networks are supposed to be able to make good predictions for - again, if a neural net is great at giving the right answer for data that it has already seen (ie. the data that it was trained with) but it's rubbish at making predictions for data that it hasn't seen before then it's not a very useful model! Having labelled training data and test data should help us ensure that we don't construct a model that suffers from "overfitting".
Whereas we have so far mostly been looking at binary classifiers that have a single output (where a value of greater than or equal to 0.5 indicates a "yes" and a value less than 0.5 indicates a "no"), here we want a model with ten output nodes - for each of the possible digits. And the 0-1 value that each output will receive will be a "confidence" value for that output. For example, if our trained network processes and image and the outputs for 0, 1, .. 7 are low (say, 0.1) the outputs for 8 and 9 are both similarly high then it indicates that the model is fairly sure that the image is either an 8 or a 9 but it is not very sure which. On the other hand, if 0..7 are low (0.1-ish) and 8 is high (say, 0.9) and 9 is in between (0.6 or so) then the model still thinks that 8 or 9 are the most likely results but, in this case, it is much more confident that 8 is the correct output.
What we know about the model at this point, for sure, is that there are 784 input neurons (for each pixel in the source data) and 10 output neurons (for each possible label for each image). What we don't know is whether we need a hidden layer or not. What we do know in this case, though, is how we can measure the effectiveness of any model that we train - because we train it using the training data and then see how well that trained model predicts the results of the test data. If our trained model gets 99% of the correct answers when we try running the test data through it then we know that we've done a great job and if we only get 10% of the correct answers for our test data then we've not got a good model!
I said earlier that one way to try to train a model is to take the approach of "start with random weights and see how well it predicts outputs for the training data then adjust weights to improve it and then run through the training data again and then adjust weights to improve it.." iterations until the model either calculates all of the outputs correctly or gets to within an acceptable range. Well, another way to approach it is to decide how many iterations you're willing to do and to just stop the training at that point. Each iteration is referred to as an "epoch" and you might decide that you will run this training process for 500 epochs and then test the model that results against your test data to see how accurate it is. Depending upon your training data, this may have the advantage that the resulting model will not have an acceptably low error rate but one advantage that it definitely does have is that the training process will end - whereas if you were trying to train a model that doesn't have any hidden layer of neurons and the training data is not linearly separable then the training process would never end if you were going to let it run until it was sufficiently accurate because it's just not possible for a model of that form to be accurate for that sort of data.
This gives us a better way to answer the question "how many layers should the model have?" because you could start with just an input layer and an output layer, with randomly generated connection weights (as we always start with), have the iterative run-through-the-input-data-and-check-the-outputs-against-the-expected-values-then-try-to-improve-the-weights-slightly-to-get-better-results process run for 500 epochs and then see how well the resulting model does as handling the test data (for each of the 10k labelled images, run them through the model and count it as a pass if the output that matches the correct digit for the image has the highest value out of all ten of the outputs and count it is a fail if that is not the case).
Since we're not looking at code here to perform all this work, you'll have to take my word for what would happen - this simple model shape would not do very well! Yes, it might predict the correct digit for some of the inputs but even if a broken clock is right twice a day!
This indicates that we need a different model shape and the only other shape that we've seen so far has an additional "hidden layer" between the input layer and the output layer. However, even this introduces some questions - first, if we add a hidden layer then how many neurons should it have in it? The XOR example has two neurons in the input layer, two neurons in the hidden layer and one neuron in the output layer - does this tell us anything about how many we should use here? Secondly, is there any reason why we have to limit ourselves to a single hidden layer? Could there be any advantages to having multiple hidden layers (say, the input layer, a first hidden layer, a second hidden layer, the output layer)? If so, should each hidden layer have the same number of neurons as the other hidden layers or should they be different sizes?
Well, again, on the one hand, we now have a mechanism to try to answer these questions - we could guess that we want a single hidden layer that has 100 neurons (a number that I've completely made up for the sake of an example) and try training that model for 500 epochs* using the training, then see how accurate the resulting model is at predicting the results of the test data. If the accuracy seems acceptable then you could say that you've found a good model! But if you want to see if the accuracy could be improved then you might try repeating the process but with 200 neurons in the hidden layer and trying again - or maybe even reducing it down to 50 neurons in the hidden layer to see how that impacts the results! If you're not happy with any of these results then maybe you could try adding a second hidden layer and then playing around with how many neurons are in the first layer and the second layer!
* (This 500 value is also one that I've just made up for sake of example right now - deciding how many iterations to attempt when training the model may come down to how much training data that you have because the more data that there is to train with, the longer each iteration will take.. so if 500 epochs can be completed in a reasonable amount of time then it could be a good value to use but if it takes an entire day to perform those 500 iterations then maybe a small number would be better!)
One thing to be aware of when adding hidden layers is that the more layers that there are, the more calculations that must be performed as the model is trained. Similarly, the more neurons that there are in the hidden layers, the more calculations there are that must be performed for each training iteration/epoch. If you have a lot of training data then this could be a concern - it's tedious to fiddle around with different shapes of models if you have to wait hours (or even days!) each time that you want to train a model in a new configuration. And so erring on the side of fewer layers and few neurons in those layers is a good starting point - if you can get good results from that then you will get over the finish line sooner!
To finally offer some concrete advice, I'm going to quote a Stack Overflow answer that repeats a rule of thumb that I've read in various other places:
(i) number of hidden layers equals one;
and (ii) the number of neurons in that layer is the mean of the neurons in the input and output layers.
This advice recommends that we start with a single hidden layer and that it have 397 neurons (which is the average of the number of neurons in the input layer = 28 * 28 pixels = 784 inputs and the number of neurons in the output layer = 10).
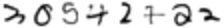
Using the MNIST training data to train a neural network of this shape (784 inputs, 387 neurons in hidden layer, 10 outputs) across 10 epochs will result in a model that has 95.26%* accuracy when the test data is run through it. Considering what some of these handwritten digits in the test data look like, I think that that is pretty good!
* (I know this because I went through the process of writing the code to do this a few years ago - I was contemplating using it as part of a series of posts about picking up F# if you're a C# developer but I ran out of steam.. maybe one day I'll pick it back up!)
To try to put this 95.26% accuracy into perspective, the PDF "Formal Derivation of Mesh Neural Networks with Their Forward-Only Gradient Propagation" claims that the MNIST data has an "average human performance of 98.29%"* (though there are people on Reddit who find this hard to believe and that it is too low) while the state of the art error rate for MNIST (where, presumably, the greatest machine learning minds of our time compete) is 0.21%, which indicates an accuracy of 99.71% (if I've interpreted the leaderboard's information correctly!).
* (Citing P. Simard, Y. LeCun, and J. Denker, "Efficient pattern recognition using a new transformation distance" in Advances in Neural Information Processing Systems (S. Hanson, J. Cowan, and C. Giles, eds.), vol. 5, pp. 50–58, Morgan-Kaufmann, 1993)
Note: If I had trained a model that had TWO hidden layers where, instead of there being a single hidden layer whose neuron count was 1/2 x number-of-inputs-plus-number-of-outputs, the two layers had 2/3 and 1/3 x number-of-inputs-plus-number-of-outputs then the accuracy could be increased to 97.13% - and so the advice above is not something set in stone, it's only a guideline or a starting point. But I don't want to get too bogged down in this right now as the section just below talks more about multiple hidden layers and about other options, such as pre-processing of data; with machine learning, there can be a lot of experimentation required to get a "good enough" result and you should never expect perfection!
Other shapes of network and other forms of processing
The forms of neural network that I've shown above are the most simple (regardless of how many hidden layers there are - or aren't) but there is a whole range of variations that offer tools to potentially improve accuracy and/or reduce the amount of time required to train them. This is a large topic and so I won't go deeply into any individual possibility but here are some common variations..
Firstly, let's go back to thinking about those hidden layers and how many of them that you might want. To quote part of a Quora answer:
There is a well-known problem of facial recognition, where computer learns to detect human faces. Human face is a complex object, it must have eyes, a nose, a mouth, and to be in a round shape, for computer it means that there are a lot of pixels of different colours that are comprised in different shapes. And in order to decide whether there is a human face on a picture, computer has to detect all those objects.
Basically, the first hidden layer detects pixels of light and dark, they are not very useful for face recognition, but they are extremely useful to identify edges and simple shapes on the second hidden layer. The third hidden layer knows how to comprise more complex objects from edges and simple shapes. Finally, at the end, the output layer will be able to recognize a human face with some confidence.
Basically, each layer in the neural network gets you farther from the input which is raw pixels and closer to your goal to recognize a human face.
I've seen various explanations that describe hidden layers as being like feature inputs for increasingly specific concepts (with the manager decision example, the two input neurons represented very specific features that we had chosen for the model whereas the suggestion here is that the neurons in each hidden layer represent features extracted from the layer before it - though these features are extracted as a result of the training process and they may not be simple human-comprehendible features, such as "strategic value").. but I get the impression that this is something of an approximation of what's going on. In the face detection example above, we don't really know for sure that the third hidden layer really consists of "complex objects from edges and simple shapes" - that is just (so far as I understand it) an approximation to give us a feeling of intuition about what is going on during the training process.
It's important to note that ALL that is happening during the training is fiddling of neuron connection weights such that the known inputs of the training data get closer to producing the expected outputs in the training data corresponding to those inputs! While we might be able to understand and describe this as a mathematical process (and despite these neural network structures having been inspired by the human brain), we shouldn't fool ourselves into believing that this process is "thinking" and analysing information in the same way that we do! I'll talk about this a little more in the section "The dark side of machine learning predictions a little further down".
Another variation used is what "activation function" is used for neurons in each layer. When I described the sigmoid function earlier, which took the sums of the neurons in the previous layer multiplied by their connection weights and then applied a formula to squash that value into the 0-1 range; that was an activation function. In the XOR example earlier, the sigmoid function was used as the activation function for each neuron in the hidden layer and each neuron in the output layer. But after I did this, I had to look at the final output values and say "if it's 0.5 or more then consider it to be a 1 and if it's less than 0.5 then consider it to be a 0".. instead of doing that, I could have used a "step function" for the output layer that would be similar to the sigmoid function but which would have sharp cut off points (for either 0 or 1) instead of a nice smooth curve*.
* (The downside to using a step function for the output of a binary classifier is that you lose any information about how confident the result is if you only get 0 or 1; for example, an output of 0.99 indicates a very confident >= 0.5 result while an output of 0.55 is still >= 0.5 and so indicates a 1 result but it is a less confident result - if the information about the confidence is not important, though, then a step function could have made a lot of sense in the XOR example)
Another common activation function that appears in the literature about neural networks is the "Rectified Linear Unit (ReLU)" function - it's way out of the scope of this post to explain why but if you have many hidden layers then you can encounter difficulties if you use the sigmoid function in each layer and the ReLU can ease those woes. If you're feeling brave enough to dig in further right now then I would recommend starting with "A Gentle Introduction to the Rectified Linear Unit (ReLU)".
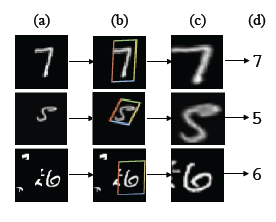
Finally, there are times when changing your model isn't the most efficient way to improve its accuracy. Sometimes, cleaning up the data can have a more profound effect. For example, there is a paper Spatial Transformer Networks (PDF) that I saw mentioned in a StackOverflow answer that will try to improve the quality of input images before using them to train a model or to make a prediction on test data or not-seen-before data.
In the case of the MNIST images, it can be seen to locate the area of the image that looks to contain the numeral and to then rotate it and stretch it such that it will hopefully reduce the variation between the many different ways that people write numbers. The PDF describes the improvements in prediction accuracy and also talks about using the same approach to improve recognition of other images such as street view house numbers and even the classification of bird species from images. (Unfortunately, while the StackOverflow answer links to a Google doc with further information about the performance improvements, it's a private document that you would have to request access to).
The approach to image data processing can also be changed by no longer considering the raw pixels but, instead, deriving some information from them. One example would be to look at every pixel and then see how much lighter or darker it is than its surrounding pixels - this results in a form of edge detection and it can be effective at reducing the effect of light levels in the source image (in the case of a photo) by looking at the changes in brightness, rather than considering the brightness on a pixel-by-pixel basis. This changes the source data to concentrate more on shapes within the images and less on factors such as colours - which, depending upon the task at hand, may be appropriate (in the case of recognising handwritten digits, for example, whether the number was written in red or blue or green or black shouldn't have any impact on the classification process used to predict what number an image contains).

(In my post from a couple of years ago, "Face or no face", I was using a different technique than a neural network to train a model to differentiate between images that were faces and ones that weren't but I used a similar method of calculating "intensity gradients" from the source data and using that to determine "histograms of gradients (HoGs)" - I won't repeat the details here but that approach resulted in a more accurate model AND the HoGs data for each image was smaller than the raw pixel data and so the training process was quicker; double win!)
The next thing to introduce is a "convolutional neural network (CNN)", which is a variation on the neural network model that adds in "convolution layers" that can perform transformations on the data (a little like the change from raw colour image data to changes-in-brightness data, as shown in the edge detection picture above) though they will actually be capable of all sorts of types of alteration, all with multiple configuration options to tweak how they may be applied. But..
a CNN learns the values of these filters on its own during the training process
(From the article "An Intuitive Explanation of Convolutional Neural Networks")
.. and so the training process for this sort of model will not just experiment with changing the weights between neurons to try to improve accuracy, it will also try running the entire process over and over again with variations on the convolutional layers to see if altering their settings can produce better results.
To throw another complication into the mix - as I mentioned earlier, the more hidden layers (and the more neurons that each layer has), the more calculations that are required by the training process and so the slower that training a model will be. This is because every input neuron is connected to every neuron in the first hidden layer, then every neuron in the first hidden layer is connected to every neuron in the second hidden layer, etc.. until every neuron in the last hidden layer is connected to every neuron in the output layer - which is why the number of calculations expands massively with each additional layer. These are described as "fully-connected layers". But there is an alternative; the imaginatively-named approach "sparsely connected layers". By having fewer connections, the necessary calculations are fewer and the training time should be shorter. In a neural net, there are commonly a proportion of connections that have a great impact on the accuracy of the training model and a proportion that have a much lower (possibly even zero) effect. Removing these "lower value" connections is what allows us to avoid a lot of calculations/processing time but identifying these connections is a complex subject. I'm not even going to attempt to go into any detail in this post about how this may be achieved but if you want to know more about the process of intelligently selecting what connections to use, I'll happily direct you to the article "The Sparse Future of Deep Learning!
One final final note for this section, though: in most cases, more data will get you superior results in comparison to trying to eke out better results from a "cleverer" model that is trained with less data. If you have a model that seems decent and you want to improve the accuracy, if you have the choice between spending time obtaining more quality data (where "quality" is an important word because "more data" isn't actually useful if that data is rubbish!) or spending time fiddling with the model to try to get a few more percentage points of accuracy, generally you will be better to get more data. As Peter Norvig, Google's Director of Research, was quoted as saying (in the article "Every Buzzword Was Born of Data"):
We don't have better algorithms. We just have more data.
The dark side of machine learning predictions
The genius of machine learning is that it can take historical data (what inputs lead to what output) and produce a model that can use that information to make an output prediction for a set of inputs that it's never seen before.
A big downfall of machine learning is that all it is doing is taking historical data and producing a model that uses that information to predict an output for a set of inputs that it's never seen before.
In an ideal world, this wouldn't be a downfall because all decisions would have been made fairly and without bias. However.. that is very rarely the case and when a model is trained using historical data, you aren't directly imbuing it with any moral values but it will, in effect, exhibit any biases in the data that was used to train it.
One of the earliest examples that stick in my mind of this was of a handheld camera that had blink detection to try to help you get a shot where everyone has their eyes open. However, the data used to train the model used photos of caucasian people, resulting in an Asian American writing a post "Racist Camera! No, I did not blink... I'm just Asian!" (as reported on PetaPixel) as the camera "detected" that she was blinking when she wasn't.
And more horrifying is the article from the same site "Google Apologizes After Photos App Autotags Black People as 'Gorillas'" which arose from Flickr adding an auto-tagging facility that would make suggestions as to what it recognised in your photos. Again, this comes down to the source data that was used to train the models - and it's not to suggest that the people sourcing and using this data (which could well be two groups of people; one that collects and tags sets of images and a second group that presumes that that labelled data is sufficiently extensive and representative) are unaware of the biases that it contains. As with life, there are always unconscious biases and the only way to tackle them is to be aware of them and try as best you can to eradicate them!
Another example is that, a few years ago, Amazon toyed with introducing a resume-screening process using machine learning - where features were extracted from CVs (the features would be occurrences of a long, known list of words or phrases in this case, as opposed to the numeric values in the manager decision example of the pixel brightnesses in the MNIST example) and the recruitment outcomes (hired / not-hired) from historical data to train a model. However, all did not go to plan. Thankfully, they didn't just jump into the deep end and accept the results of the model when they received new CVs; instead, they ran them through the model and performed the manual checks, to try to get an idea of whether the model was effective or not. I'm going to take some highlights from the article "Amazon built an AI tool to hire people but had to shut it down because it was discriminating against women", so feel free to read that if you want more information. The upshot is that historically there had been many more CVs submitted by men than women, which resulted in there being many more "features" present on male CVs that resulted in a "hire them!" result. As I described before, when a neural network (presuming that Amazon was using such an approach) is presented with many features, it will naturally work out which have a greater impact on the final outcome and the connection weights for these input neurons will be higher. What I didn't describe at that point is that the opposite also happens - features that are found to have a negative impact on the final outcome will not just be given a smaller weight, they will be given a negative weight. And since this model was effectively learning that men are more likely to be hired and women are less likely, the model that it ended up with gave greater positive weight to features that indicated that the CV was for a male and negative weight to features that indicated that the CV was for a female, such as a mention of them being a "women's chess club captain" or even if they had attended one of two all-women's colleges (the name of which had presumably been in the list of known words and phrases that would have been used as features - and which would not have appeared on any man's CV). The developers at Amazon working on this project made changes to try to avoid this issue but they couldn't be confident that other biases were not having an effect and so the project was axed.
There are, alas, almost certainly always going to be issues with bias when models are trained in this manner - hopefully, it can be reduced as training data sets become more representative of the population (for cases of photographs of people, for example) but it is something that we must always be aware of. I thought that some industries were explicitly banned from applying judgements to their customers using a non-accountable system such as the neural networks that we've been talking about but I'm struggling to find definitive information. I had it in my head that the UK car insurance market was not allowed to produce prices from a system that isn't transparent and accountable (eg. it would not be acceptable to say "we will offer you this price because the computer says so" as opposed to a "decision-tree-based process" where it's essentially like a big flow chart that could be explained in clear English, where the impacts on price for each decision are based on statistics from previous claims) but I'm also unable to find any articles stating that. In fact, sadly, I find articles such as "Insurers 'risk breaking racism laws'" which describe how requesting quotes from some companies, where the only detail that varies between them is the name (a traditionally-sounding white English name compared to another traditional English - but not traditionally white - name, such as Muhammad Khan), results in wildly different prices being offered.
Talking of training neural nets with textual data..
In all of my descriptions before the previous section, I've been using examples where the inputs to the model as simple numbers -
- Zeros and ones for the AND, OR, XOR cases
- Numeric 0..1 value ranges for the features of the manager decision example (which were, if we're being honest, oversimplifications - can you really reliably and repeatedly rate the strategic importance to the company of a single feature in isolation? But I digress..)
- Pixel brightness values for the MNIST example, which are in the range 0-255 and so can easily be reduced down to the 0-1 range
- I mentioned brightness gradients (rather than looking at the intensity of individual pixels, looking at how much brighter or darker they are compared to surrounding pixels) and this also results in values that are easy to squeeze into the 0-1 range
However, there are all sorts of data that don't immediately look like they could be represented as numeric values in the 0-1 range. For example, above I was talking about analysis of CVs and that is purely textual content (ok, there might be the odd image and there might be text content in tables or other layouts but you can imagine how simple text content could be derived from that). There are many ways that this could be done but one easy way to imagine it would be to:
- Take a bunch of documents that you want to train a classifier on (to try to avoid the contentiousness of the CV example, let's imagine that it's a load of emails and you want to automatically classify them as "spam", "company newsletter", "family updates" or one of a few other categories
- Identify every single unique word across all of the documents and record them in one big "master list"
- Go through each document individually and..
- Split it into individual words again
- Go through each word in the master list and calculate a score by counting how many times it appears in the current document divided by how many words there are in the document (the smaller that this number is, the less common that it is and, potentially, the more interesting it is in differentiating one document from another)
- For each document, you now have a long list of numbers in the range 0-1 and you could potentially use this list to represent the features of the document
- Each list of numbers is the same length for each document because the same master list of words was used (this is vitally important, as we will see shortly)
- The list of numbers that is now used to describe a given document is called a "vector"
One problem here is that the vocabulary used throughout these emails could be very large, meaning that the master list would be very large and the list of numbers for each document equally large. The input layer of a neural network that we would train using this data would have to have as many neurons as there are entries in these lists. This might not necessarily be a problem because it is possible to train large neural networks - but the larger that they are, the longer that it takes.
There are almost certainly going to be lots of words that appear that will have no effect on the classification of an email - words like "a" and "the", for example. As discussed earlier, this is also not strictly a problem because features that have little effect on the classification of data will naturally end up with low connection weights in the final trained model. However, it feels wasteful to throw data into the mix that we know isn't going to be useful but is certainly going to slow down the training process by forcing it to perform many more calculations. One approach is to ignore "stop words" when generating the master list of all words in the source data -
Stopwords are the words in any language which does not add much meaning to a sentence. They can safely be ignored without sacrificing the meaning of the sentence.
(From "Stop Words in NLP")
This is a common approach and lists of stop words are freely available - but it's important to be aware that they are language-dependent; English stop words are not the same as French stop words, for example, and you will need to consider this if you're not always working with English language data!
Another approach is to take advantage of the fact that the calculation above generates smaller values for words that are potentially more relevant (because the word "the" is likely to appear many times in a document, if you divide the number of times that it appears by the total number of words in the document then that value will normally be much higher than if you divided the number of time that a less common word - like "bonus" - appeared in a document by the total number of words in that document). You might decide to discard, say, 20% of the words by looking at which of them appear in the documents with a high score and removing those words from the master list (and removing the corresponding entries from each of the lists of numbers that represents each document). By doing so, you would likely end up removing the stop words without having to have had to start with a known list of stop words to get rid of! (Again, this sort of process is language-dependent because words that are common in one language are different in another language and this sort of approach will work best if all of the documents used as training data are written in the same language).
This still leaves us with many more distinct words than is probably optimal. For example, if the document text is split into words in a very simple manner (such as breaking on whitespace) then you may have an email that is a thrilling update about Mark's cat, while another email may be talking about Henry's cats - in the context of trying to working out what an email is talking about, is there any meaningful distinction between "cat" (singular) and "cats" (plural)? Probably not. And so adding in a pre-processing step to the act of splitting the text into individual words could help reduce the number of distinct words further by grouping words that are probably equivalent. An example of this is the Snowball Stemmer which performs simple transformations such as lower-casing content, removing punctuation and removing common endings from words so that different forms of verbs are combined into the same word; eg.
Dan's cats like going to the park
.. becomes
dan cat like go to the park
(There is unlikely to be any benefit to considering the words "Dan's" and "Dan" as different features, just as there is little benefit to considering "cat" and "cats" as unique features).
Note that the Snowball Stemmer is also language-dependent and so you need to know what language the text that you're working with is in - again, if you're lucky enough to be dealing with an entirely English set of training documents then that's fine.. though the nltk.stem.snowball Python package used in the link above has support for different languages, so long as you tell it which language you want it to use.
(Shameless plug: Some years ago, I wrote my own interpretation of a Full Text Indexer - which actually powers the site search on this blog! - and core functionality for that include "tokenising" and "token normalising", which are the splitting of a string of text into individual words and the transformation of those tokens such that equivalent tokens like "Cat" and "cat" and "cats" are all reduced down to a single string; if you wanted to see one way to do this sort of work in C# then you could poke around my FullTextIndexer GitHub repo or read some of the articles listed in my "Full Text Indexer Post Round-up".. I would be remiss if I didn't mention that there are plenty of other libraries for .NET that have been written in the last ten years that are quite likely more featureful and optimised, but this is my blog and so if I want to link to my own code instead then I will! :))
In general, it would make sense to apply the stemming logic before culling the most common words from the list of features, so that you have an accurate picture of what words are true most "interesting" (ie. uncommon).
When I described the way that you might approach an MNIST classifier earlier, I explained that you could get a surprisingly accurate model by flattening out the 28x28 pixel image into one long 784 list of values - seemingly discarding structural information about where the pixels appear in relation to each other in two dimensions. What I've described just now, regarding the words-as-features, is similar in some ways as it is also discarding information about how words appear in relation to each other; the features that are produced are all solely based on individual words in isolation.
However, with natural language, the words that appear around a given word can make a big difference - the word "new" represents an entirely different concept when it talks about releasing a "new feature" for some software to when it is used in the city name "New York". As such, depending upon the data and the task in hand, it will often result in a more accurate model if the features extracted from textual content are not only individual words but also phrases, such as adjacent pairs of words (like "New York") or concurrent runs of three words or even more. Doing so will mean that the number of possible features grows again (it's not just a master list of individual words any longer, it's now a list of words and phrases - and one of the decisions that you will have to make is how long you allow the extracted phrases to be. The longer that they can be, the more possible features that you will produce (which will make model-training slower). The shorter that they can be, the fewer features there will be (and so model-training will be faster) but you risk missing out on vital context if the limit is too low (and so you might end up training models relatively quickly but finding that their accuracy is low for the task at hand).
With this knowledge, you could now picture a neural network model because you can take the documents in your training data and convert them into vectors (which are, as a reminder, simply lists of numeric values) and each vector will be the same length (ie. it will have the same number of values in it). The length of this vector will determine how large the input layer is in the neural network because there must be as many neurons in the input layer as the document vectors are long (if, say, the master list of words used to generate the document vectors had 10,000 unique entries then each document will have been translated into a vector with 10,000 values in it and the input layer for the neural network will have to have 10,000 nodes).
This brings us to an important decision.. we will have to decide how large the document vectors should be - before, I said that you might discard the least interesting 20% of the words but that was just an example figure that I made up on the spot. I started this example by saying that you may wish to classify emails into a particular set of categories but you will have had to decide on what exactly is in that "what type of email is this" list before you can create a model and you'll need to have manually classified every document in your training data before you can start training a neural net to do the same work. The idea behind training a classifier is that it can predict a category for data (eg. an email) that it's never seen before but it needs historical labelled data to do that, which is what this pre-categorised training data will be.
All of the variables that have been mentioned - the percentage of "non-interesting" words (or "tokens", as they are often referred to) that are discarded, the maximum number of tokens that may be combined into one to produce larger features (like the "New York" example), the number of outputs (which is the number of categories that emails may be assigned to - which will dictate how many neurons in the output layer; one per category), how many hidden layers that your model should have (and how large those layers should be).. these will all impact the training process and are known as "hyperparameters". Changing some of them may result in large changes (good or bad) in the accuracy of the trained model while changing others may not have much impact at all. As I said before, part of working with machine learning is in experimenting with different models and different hyperparameters to see what works well for your data and what doesn't!
Side note: The process that I've described above (about producing a "master list" of words and phrases) is a sort of simplified/bastardised of TF-IDF ("term frequency-inverse document frequency" - ie. how often do individual words appear in a document relative to the total number of words in that document), for which there is a nice intro at "Understanding TF-ID: A Simple Introduction". And when I spoke about the process of combining multiple individual words together to produce new tokens (such as "New York"), those new tokens are referred to as "n-grams" - so if you want to find out more about all this then there is plenty of great information out there!
Other types of machine learning
Almost the entirety of this lengthy post has been about neural network classifiers but it's definitely worth mentioning that these are not the only type of machine learning techniques.
The first example that I want to talk about is "document similarity" - say you have 100,000 text documents and you are fairly sure that some of them are very nearly duplicates of each other (maybe one is a technical spec for an audio amplifier from 2019 and another is a revision of that document from 2020 that includes some corrections but is basically the same), how would you find these similar documents? Well, a good starting point would be by using the textual content feature extraction described in the previous section - ie. converting each document into a vector. When that is done, it's actually quite simple to come up with an approximate "distance measurement". If you imagine a load of 2D points on a graph, you can easily measure the distance between any two points by using Pythagorean theorem; take the horizontal difference between the two points and square it, add that to the vertical difference between them squared, then square root the result. This same approach works for points in a 3D world. And the same principle works for points with any number of dimensions - and this is how we could imagine our vectors that have been generated from each document, as points in some crazy world with many, many dimensions. We can measure the distances between pairs of these points and pairs that are relatively close to each other are likely to correspond to documents that are fairly similar in content, while pairs of points that are further away will correspond to documents that are less similar to each other.
Now, this doesn't actually involve any machine learning - it's just extracting features from documents and then measuring the distances between every single pair of points. If you only have 100 documents then these calculations can probably be performed so quickly that it wouldn't pose any sort of problem but if we go back to imagining 100,000 documents (or even imagining millions of documents, if not more!) then calculating the distances between every single pair of documents in that list could become a gargantuan task (as in, performing the calculations in a "brute force" approach - where every single distance is individually calculated - could potentially take a computer longer to compute than you have left to live, which would be very sad). There are clever machine learning algorithms that work out how to approximate these calculations such that the brute force approach is not necessary while still ensuring that document similarity measures for all of your data remain attainable (one such algorithm is "Hierarchical Navigable Small World (HNSW)", which is way too technical for me to do anything about but mention here in passing). Something interesting to note about this technique is that it is an example of "unsupervised" learning - when we looked at the MNIST (handwritten digit recognition) example earlier, that required that the input data was all labelled so that the machine could learn how the images compared or differed to each other - in this case, though, there is no such labelling required; we just tell the computer to go off and work out on its own what documents look like other documents!
(Last year, I wrote a post about how I was using a C# machine learning library that a company that I used to work for published to automatically generate "You may also be interested in" links for each of my blog posts and that used some of the same techniques described here; the FastText algorithm automates the extraction of features from textual data and HNSW calculates distances between the document vectors - I don't actually have anywhere near enough posts on my blog for this to be necessary, I just wanted to try it for fun! If you want to find out more, see "Automating suggested / related posts links for my blog")
The next example is another form of binary classifier. I mentioned earlier my post "Face or no face", where I wanted to write code that could look at a photo and identify areas in it that appeared to be people's faces. There was a bunch of pre-processing to take a colour picture, then a very rough algorithm was run to find areas that might potentially be faces - this would return many false positives (ie. sections of a photo that were not faces) and I trained a Support Vector Machine (SVM) to be able to predict with much greater accuracy whether these image subsections were indeed faces or not. An SVM is trained by giving it a large list of labelled points (where a point doesn't have to be 2D or 3D, it can have many dimensions - so its' vectors again, in other words) and leaving it to try to work out a way to split those points so that all of the points on one side of the line are of one category and all of the points on the other side are of another category. We could train an SVM with the data from the manager decision example from earlier - its training data would be the historical list of 2D points (where the dimensions represented "strategic value to the company" and "percentage that customer will pay for feature development cost") and whether the manager gave a yes or no answer and the SVM would try to find a line that splits (or "delineates") those historical points. In a somewhat comparable way to the training of a neural network, it will pick a line at random, see how well or poorly that line delineates the results, adjusts the line to try to improve the situation and then repeats and repeats until it manages to split the data effectively. The vectors for the face-or-no-face code were much larger than two dimensions and so it's no longer a case of finding a 1D line that splits points on a 2D plane; instead, it is (cue impressive-sounding technical terms!) a case of finding an {n-1} dimensional "hyperplane" that splits the {n} dimensional space that the vector points exist in. The training data for the face-or-no-face SVM was derived from the publicly accessible "Caltech 10, 000 Web Faces".
I first mentioned unsupervised classification right near the start of this post, where training data will consist of points that should be arranged into groups of other points that they are most similar to. The problem is that the computer has no way of coming up with a description for what this group represents and so it is less directly useful for classifying into categories as those categories don't come with titles! However, it could be feasibly be used by someone like Netflix when they want to come up with creative new categories - they could have the computer extract features from tv shows and films (where the features may actually be extracted from metadata about the programs, such as description or even public reviews) and then have it arrange them into groups, which a Netflix employee could manually poke around in to see if a theme presents itself that could be used as a new niche category. But this still feels quite nebulous and so maybe a concrete example may help. One of the hyperparameters that you will need to set is how many groups you want to be generated, so let's go back to the MNIST data and imagine that we want to give a machine-learning algorithm all of the source images and for it to split the data into ten groups (for the digits 0..9) but without giving it any labels for that source data (in contrast to the supervised learning approach that was described before). Well, one such algorithm is "t-distributed stochastic neighbour embedding (t-SNE)" and that can produce results such as the following:
(Reproduced under license terms on Kyle McDonald's Flickr album page)
The t-SNE takes vectors with 784 dimensions (since the MNIST data is a set of 28x28 pixel images) as input and returns a vector for each of them that has only two dimensions, which is how the results can be plotted on the graph above. This is known as "dimension reduction" (since the 2D vectors are essentially approximations of the original 784-dimension vectors). One that image, the labels for each of the MNIST images (ie. whether that image is the digit 0 or 1 or .. 9) are used to determine the colour to draw the point as - but this is only to illustrate the results of the t-SNE algorithm, those labels were not used as part of the training. And so it's quite amazing just how effective it is at grouping similar digits together! (If there were big groups that were full of intermingled colours then that would indicate a poor job but the fact that the groups are so distinct, with only a few outliers here and there, suggests that it's done a fantastic job!) Of course, one part of the reason that it does such a good job of separating the images for each digit is that the hyperparameter specified for the algorithm about the number of groups that it should try to identify is set to 10 - if it had been set to 3 or to 12 (or to anything else) then the groupings wouldn't have been so obviously correct.
Another unsupervised algorithm that is similar to t-SNE is "Uniform Manifold Approximation and Projection (UMAP)", which you can find available as a C# implementation (also published by the company that I worked for that released the machine learning library; Curiosity!) in case you are a .NET developer and want to try it out. The "Tester" project in there includes a binary file containing the MNIST image data and it will use this to train a model that groups together the images that it thinks are similar and then generates a bitmap of the results that looks similar to the image shown above. Nothing is forcing this algorithm to reduce the vectors to two dimensions, in case you were wondering - that also is a hyperparameter that is set to train the model. It could be set to 3 and it would generate 3-dimensional vectors that could be plotted in 3D space, rather than the 2D graph above.
So machine learning is always the most amazing-est thing, right (except when it's evil and discriminatory)?
I know that I've just written thousands of words espousing the power of machine learning but I did also start the post by giving an example of coding in a "classic approach" - summing up a list of purchases that someone has made, ensuring that the correct tax is included for each of them. This is a simple and predictable process and there would not be any benefit to trying to replace this with a machine learning system. For adding together costs and calculating tax, absolute precision is expected and known predictable rules are in place; machine-trained models will almost always have some level of error (much as we may try to tweak the model to minimise it) and they are very often difficult (if not impossible) to definitively reason about - so if someone disputed a bill that had been generated from a machine-trained model, it would be very difficult to justify why it was correct or not!
However, there are some middle grounds where you may be tempted to go one way or the other. The first example that comes to mind is that where I used to work, the CTO took the opportunity to learn how to write a Roslyn analyser by implementing a "Stop commenting out code (delete it if you don't need it - we have source control, you know!)" analyser. Roslyn (well, the ".NET Compiler Platform SDK (Roslyn APIs) if you're being pernickety) makes it easy to locate comments and to show warnings in the Error List relating to them if you want to, but how to decide whether the comment text is C# code or whether it's a useful explanatory message? He could have:
- Performed a one-off analysis of the code base and extracted all of the comments
- Taken a random subset of those comments (say 5% - it was a large codebase, so even that might have been too high!)
- Manually classified each of the comments as "code" or "not code"
- Decided on a text-based feature extraction process to translate each piece of text into a vector, resulting in a list of labelled (as either 0 for "not code" or 1 for "code") vectors
- Trained a binary classifier using those labelled vectors (perhaps splitting it up to use 70% of them as training data and 30% as test data)
- Potentially spent time fiddling with the hyperparameters used in the training until the accuracy of the model was sufficiently high, based upon the results of running the test data through it
- Exported that classifier model as C# code that the analyser could execute so that it could record warnings against comments that looked they were commented-out code
Alternatively, he could have come up with a system that tried to guess whether a comment was commented-out code or something useful by splitting it into tokens (ie. individual words and symbols), assigning a score (either positive or negative) to a set of known tokens and then adding up the total for the tokens in the comment. For example, a curly brace symbol may have a positive score since they are much more common in C# code than in English phrases. If the score is greater than a particular threshold then the analyser will decide that it's probably commented-out code and record a warning about it.
This may not be quite as easy as you might expect because you can't just assign a positive score to every keyword in the C# language otherwise comments like this:
// this should be a private class
.. might be identified as commented-out code because it contains the keywords "private" and "class", but that would be wrong! And so there would be a fine line to walk to try to get it right for at least enough of the time.
(In case you were wondering, he went with the second option and it ended up working pretty well!)
A final example is a project that I only heard about very recently and just thought that it was ingenious! PawSense will "catproof your computer" because:
When cats walk or climb on your keyboard, they can enter random commands and data, damage your files, and even crash your computer. This can happen whether you are near the computer or have suddenly been called away from it.
PawSense is a software utility that helps protect your computer from cats. It quickly detects and blocks cat typing, and also helps train your cat to stay off the computer keyboard.
This might sound like the sort of thing that you would somehow try to train a model for because surely the difference between me hammering the keys and a cat jumping on the keyboard and smashing some down could be quite subtle?? Having said that, I don't personally have any great intuition for this because the closest that my cats get to this is when they lie down too close to the keyboard and end up leaning down some weight on one of the keys near the edge - they don't actually walk across it. However, the author of this software used some simple observations that are explained in the FAQ on the site, that:
If you carefully measure cat paws, you will find that practically all cat paws are significantly larger than a typical keyboard key. When a cat first places its paw down, the cat's weight plus the momentum of the cat's movement exerts pounds of force on the keyboard, primarily through the cat's paw pads.
The cat's paw angles and toe positions also undergo complex changes while the paw lands on the keyboard. This forces keys and often key combinations down in a distinctive style of typing which includes unusual timing patterns.
Cats' patterns of overall movement in walking or lying down also help make their typing more recognizable.
So simple! And yet, when you read the briefer description from the home page:
PawSense constantly monitors keyboard activity. PawSense analyzes keypress timings and combinations to distinguish cat typing from human typing.
.. then you could be forgiven for imagining that something much more convoluted would be required and that somehow the author of this software acquired lots of sample data of him (and other humans) typing in various manners (because keyboard interaction varies hugely depending upon whether you're scrolling through a web site or if you're typing code or if you're writing prose) and compared it to lots of samples of cats interacting with a keyboard. But, thinking about it, trying to record lots of keyboard interactions by cats sounds extremely difficult to me - they like to do what they want to do and are not likely to be coerced into keyboard walking if they don't already feel in the mood to do so!
You can see, then, that it's not only programs that have an extremely simple-looking set of interactions (such as the summing of item costs and taxes) that are better done by writing a traditional algorithm, there are also lots of programs that look like they exhibit "fuzzy" or "intelligent" behaviour where there is no clever machine learning involved, it is simply a result of clever observations and experimentation by whoever designed and wrote the code. However, in cases where machine learning can shine it can be incredibly powerful - whether that is YouTube keeping you on the site longer by recommending videos to watch, whether it's an automated categorisation of incoming help desk tickets in a large company to try to get customer problems directed to the relevant departments more quickly, whether it's keeping spam emails out of your inbox or whether it's used to program a cat flap to not let a cat in if it's bringing a "gift" with it (ie. a dead bird or rodent), it makes possible things that traditional algorithms would make very difficult to do well if they could even be done at all. And while it's certainly not in all software, you might be astonished to know just how much directly contains some or interacts with services that do!
Posted at 23:44
Automating "suggested / related posts" links for my blog posts - Part 2
TL;DR
By training another type of model from the open source .NET library that I've been using and combining its results with the similarity model from last time (see Automating "suggested / related posts" links for my blog posts), I'm going to improve the automatically-generated "you may be interested in" links that I'm adding to my blog.
Improvement, in fact, sufficient such that I'll start displaying the machine-suggested links at the bottom of each post.
Where I left off last time
In my last post, I had trained a fastText model (as part of the Catalyst .NET library) by having it read all of my blog posts so that it could predict which posts were most likely to be similar to which other posts.
This came back with some excellent suggestions, like this:
Learning F# via some Machine Learning: The Single Layer Perceptron
How are barcodes read?? (Library-less image processing in C#)
Writing F# to implement 'The Single Layer Perceptron'
Face or no face (finding faces in photos using C# and AccordNET)
.. but it also produced some less good selections, like this:
Simple TypeScript type definitions for AMD modules
STA ApartmentState with ASP.Net MVC
WCF with JSON (and nullable types)
The joys of AutoMapper
I'm still not discounting the idea that I might be able to improve the results by tweaking hyperparameters on the training model (such as epoch, negative sampling rate and dimensions) or maybe even changing how it processes the blog posts - eg. it's tackling the content as English language documents but there are large code segments in many of the posts and maybe that's confusing it; maybe removing the code samples before processing would give better results?
However, fiddling with those options and rebuilding over and over is a time-consuming process and there is no easy way to evaluate the "goodness" of the results - so I need to flick through them all myself and try to get a rough feel for whether I think the last run was an improvement or not.
Introducing a new model
The premise that I wil be experimenting with is to determine what words in my post titles are "interesting" and to then order the suggested-similar posts first by a score based upon how many interesting words they share and then by the similarity score that I already have.
The model that I'll be training for this is called "TF-IDF" or "Term Frequency - Inverse Document Frequency" and it looks at every word in every blog post and considers how many times that word appears in the document (the more often, the more likely that the document relates to the word) and how many times it appears across multiple documents (the more often, the more common and less "specific" it's likely to be).
For each blog post that I'm looking for similar posts to, I'll:
- take the words from its title
- take the words from another post's title
- add together all of the TF-IDF scores for words that appear in both titles (the higher the score for each word, the greater the relevance)
- repeat until all other post titles have been compared
Taking the example from above that didn't have particularly good similar-post recommendations, the words in its title will have the following scores:
| Word | Score |
|---|---|
| Simple | 0.6618375 |
| TypeScript | 4.39835453 |
| type | 0.7873714 |
| definitions | 2.60178781 |
| for | 0 |
| AMD | 3.81998682 |
| modules | 3.96386051 |
.. so it should be clear that any other titles that contain the word "TypeScript" will be given a boost.
This is by no means a perfect system as there will often be posts whose main topics are similar but whose titles are not. The example from earlier that fastText generated really good similar-post suggestions for is a great illustration of this:
Learning F# via some Machine Learning: The Single Layer Perceptron
How are barcodes read?? (Library-less image processing in C#)
Writing F# to implement 'The Single Layer Perceptron'
Face or no face (finding faces in photos using C# and AccordNET)
All of them are investigations into some form of machine learning or computer vision but the titles share very little in common. It's likely that the prediction quality of this one will actually suffer a little with the change I'm introducing but I'm looking for an overall improvement, across the entire blog. I'm also not looking for a perfect general solution, I'm trying to find something that works well for my data (again, bearing in mind that there is a relatively small quantity of it as there are only around 120 posts, which doesn't give the computer a huge amount of data to work from).
(It's also worth noting that the way I implement this in my blog is that I maintain two lists - the manually-curated list that I had before that had links for about a dozen posts and a machine-generated list; if there are manual links present then they will be displayed and the auto-generated ones will be hidden - so if I find that I have a particularly awkward post where the machine can't find nice matches then I can always tidy it up myself by manually creating the related-post links for that post)
Implementation
Last time, I had code that was reading and parsing my blog posts into a "postsWithDocuments" list.
After training the fastText model, I'll train a TF-IDF model on all of the documents. I'll then go back round each document again, have this new model "Process" them and retrieve Frequency values for each word. These values allow for a score to be generated - since the scores depend upon how often a word appears in a given document, the scores will vary from one blog post to another and so I'm taking an average score for each distinct word.
(Confession: I'm not 100% sure that this averaging is the ideal approach here but it seems to be doing a good enough job and I'm only fiddling around with things, so good enough should be all that I need)
Console.WriteLine("Training TF-IDF model..");
var tfidf = new TFIDF(pipeline.Language, version: 0, tag: "");
await tfidf.Train(postsWithDocuments.Select(postWithDocument => postWithDocument.Document));
Console.WriteLine("Getting average TF-IDF weights per word..");
var tokenValueTFIDF = new Dictionary<string, List<float>>(StringComparer.OrdinalIgnoreCase);
foreach (var doc in postsWithDocuments.Select(postWithDocument => postWithDocument.Document))
{
// Calling "Process" on the document updates data on the tokens within the document
// (specifically, the token.Frequency value)
tfidf.Process(doc);
foreach (var sentence in doc)
{
foreach (var token in sentence)
{
if (!tokenValueTFIDF.TryGetValue(token.Value, out var freqs))
{
freqs = new();
tokenValueTFIDF.Add(token.Value, freqs);
}
freqs.Add(token.Frequency);
}
}
}
var averagedTokenValueTFIDF = tokenValueTFIDF.ToDictionary(
entry => entry.Key,
entry => entry.Value.Average(), StringComparer.OrdinalIgnoreCase
);
Now, with a couple of helper methods:
private static float GetProximityByTitleTFIDF(
string similarPostTitle,
HashSet<string> tokenValuesInInitialPostTitle,
Dictionary<string, float> averagedTokenValueTFIDF,
Pipeline pipeline)
{
return GetAllTokensForText(similarPostTitle, pipeline)
.Where(token => tokenValuesInInitialPostTitle.Contains(token.Value))
.Sum(token =>
{
var tfidfValue = averagedTokenValueTFIDF.TryGetValue(token.Value, out var score)
? score
: 0;
if (tfidfValue <= 0)
{
// Ignore any tokens that report a negative impact (eg. punctuation or
// really common words like "in")
return 0;
}
return tfidfValue;
});
}
private static IEnumerable<IToken> GetAllTokensForText(string text, Pipeline pipeline)
{
var doc = new Document(text, pipeline.Language);
pipeline.ProcessSingle(doc);
return doc.SelectMany(sentence => sentence);
}
.. it's possible, for any given post, to sort the titles of the other posts according to how many "interesting" words (and how "interesting" they are) they have in common like this:
// Post 82 on my blog is "Simple TypeScript type definitions for AMD modules"
var post82 = postsWithDocuments.Select(p => p.Post).FirstOrDefault(p => p.ID == 82);
var title = post82.Title;
var tokenValuesInTitle =
GetAllTokensForText(NormaliseSomeCommonTerms(title), pipeline)
.Select(token => token.Value)
.ToHashSet(StringComparer.OrdinalIgnoreCase);
var others = postsWithDocuments
.Select(p => p.Post)
.Where(p => p.ID != post82.ID)
.Select(p => new
{
Post = p,
ProximityByTitleTFIDF = GetProximityByTitleTFIDF(
NormaliseSomeCommonTerms(p.Title),
tokenValuesInTitle,
averagedTokenValueTFIDF,
pipeline
)
})
.OrderByDescending(similarResult => similarResult.ProximityByTitleTFIDF);
foreach (var result in others)
Console.WriteLine($"{result.ProximityByTitleTFIDF:0.000} {result.Post.Title}");
The top 11 scores (after which, everything has a TF-IDF proximity score of zero) are these:
7.183 Parsing TypeScript definitions (functional-ly.. ish)
4.544 TypeScript State Machines
4.544 Writing React components in TypeScript
4.544 TypeScript classes for (React) Flux actions
4.544 TypeScript / ES6 classes for React components - without the hacks!
4.544 Writing a Brackets extension in TypeScript, in Brackets
0.796 A static type system is a wonderful message to the present and future
0.796 A static type system is a wonderful message to the present and future - Supplementary
0.796 Type aliases in Bridge.NET (C#)
0.796 Hassle-free immutable type updates in C#
0.000 I love Immutable Data
So the idea is to then use the fastText similarity score when deciding which of these matches is best.
There are all sorts of ways that these two scoring mechanisms could be combined - eg. I could take the 20 titles with the greatest TF-IDF proximity scores and then order them by similarity (ie. which results the fastText model thinks are best) or I could reverse it and take the 20 titles that fastText thought were best and then take the three with the greatest TF-IDF proximity scores from within those. For now, I'm using the simplest approach and ordering by the TF-IDF scores first and then by the fastText similarity model. So, from the above list, the 7.183-scoring post will be taken first and then 2 out of the 5 posts that have a TF-IDF score of 4.544 will be taken, according to which ones the fastText model thought were more similar.
Again, there are lots of things that could be tweaked and fiddled with - and I imagine that I will experiment with them at some point. The main problem is that I have enough data across my posts that it's tedious looking through the output to try to decide if I've improved things each time I make change but there isn't enough data that the algorithms have a huge pile of information to work on. Coupled with the fact that training takes a few minutes to run and I have recipe for frustration if I obsess too much about it. Right now, I'm happy enough with the suggestions and any that I want to manually override, I can do so easily.
Trying the code yourself
If you want to try out the code, you can find a complete sample in the "SimilarityWithTitleTFIDF" project in the solution of this repo: BlogPostSimilarity.
Has it helped?
Let's return to those examples that I started with.
Good suggestions from last time:
Learning F# via some Machine Learning: The Single Layer Perceptron
How are barcodes read?? (Library-less image processing in C#)
Writing F# to implement 'The Single Layer Perceptron'
Face or no face (finding faces in photos using C# and AccordNET)
Less good suggestions:
Simple TypeScript type definitions for AMD modules
STA ApartmentState with ASP.Net MVC
WCF with JSON (and nullable types)
The joys of AutoMapper
Now, the not-very-good one has improved and has these offered:
Simple TypeScript type definitions for AMD modules
Parsing TypeScript definitions (functional-ly.. ish)
TypeScript State Machines
Writing a Brackets extension in TypeScript, in Brackets
.. but, as I said before, the good suggestions are now not as good as they were:
How are barcodes read?? (Library-less image processing in C#)
Face or no face (finding faces in photos using C# and Accord.NET)
Implementing F#-inspired "with" updates for immutable classes in C#
A follow-up to "Implementing F#-inspired 'with' updates in C#"
There are lots of suggestions that are still very good - eg.
Creating a C# ("Roslyn") Analyser - For beginners by a beginner
Using Roslyn to identify unused and undeclared variables in VBScript WSC components
Locating TODO comments with Roslyn
Using Roslyn code fixes to make the "Friction-less immutable objects in Bridge" even easierMigrating my Full Text Indexer to .NET Core (supporting multi-target NuGet packages)
Revisiting .NET Core tooling (Visual Studio 2017)
The Full Text Indexer Post Round-up
The NeoCities Challenge! aka The Full Text Indexer goes client-side!Dependency Injection with a WCF Service
Ramping up WCF Web Service Request Handling.. on IIS 6 with .Net 4.0
Consuming a WCF Web Service from PHP
WCF with JSON (and nullable types)Translating VBScript into C#
VBScript is DIM
Using Roslyn to identify unused and undeclared variables in VBScript WSC components
If you can keep your head when all about you are losing theirs and blaming it on VBScript
.. but still some less-good suggestions, like:
Auto-releasing Event Listeners
Writing React apps using Bridge.NET - The Dan Way (Part Three)
Persistent Immutable Lists - Extended
Extendable LINQ-compilable MappersProblems in Immutability-land
Language detection and words-in-sentence classification in C#
Using Roslyn to identify unused and undeclared variables in VBScript WSC components
Writing a Brackets extension in TypeScript, in Brackets
However, having just looked through the matches to try to find any really awful suggestions, there aren't many that jump out at me. And, informal as that may be as a measure of success, I'm fairly happy with that!
Posted at 21:56
Automating "suggested / related posts" links for my blog posts
TL;DR
Using the same open source .NET library as I did in my last post (Language detection and words-in-sentence classification in C#), I use some of its other machine learning capabilities to automatically generate "you may also be interested in" links to similar posts for any given post on this blog.
The current "You may also be interested in" functionality
This site has always had a way for me to link related posts together - for example, if you scroll to the bottom of "Learning F# via some Machine Learning: The Single Layer Perceptron" then it suggests a link to "Face or no face (finding faces in photos using C# and Accord.NET)" on the basis that you might be super-excited into my fiddlings with computers being trained how to make decisions on their own. But there aren't many of these links because they're something that I have to maintain manually. Firstly, that means that I have to remember / consider every previous post and decide whether it might be worth linking to the new post that I've just finished writing and, secondly, I often just forget.
There are models in the Catalyst library* that make this possible and so I thought that I would see whether I could train it with my blog post data and then incorporate the suggestions into the final content.
* (Again, see my last post for more details on this library and a little blurb about my previous employers who are doing exciting things in the Enterprise Search space)
Specifically, I'll be using the fastText model that was published by Facebook's AI Research lab in 2015 and then rewritten in C# as part of the Catalyst library.
Getting my blog post articles
When I first launched my blog (just over a decade ago), I initially hosted it somewhere as an ASP.NET MVC application. Largely because I wanted to try my hand at writing an MVC app from scratch and fiddling with various settings, I think.. and partly because it felt like the "natural" thing to do, seeing as I was employed as a .NET Developer at the time!
To keep things simple, I had a single text file for each blog post and the filenames were of a particular format containing a unique post ID, date and time of publishing, whether it should appear in the "Highlights" column and any tags that should be associated with it. Like this:
1,2011,3,14,20,14,2,0,Immutability.txt
That's the very first post (it has ID 1), it was published on 2011-03-14 at 20:14:02 and it is not shown in the Highlights column (hence the final zero). It has a single tag of "Immutability". Although it has a ".txt" extension, it's actually markdown content, so ".md" would have been more logical (the reason why I chose ".txt" over ".md" will likely remain forever lost in the mists of time!)
A couple of years later, I came across the project neocities.org and thought that it was a cool idea and did some (perhaps slightly hacky) work to make things work as a static site (including pushing the search logic entirely to the client) as described in The NeoCities Challenge!.
Some more years later, GitHub Pages started supporting custom domains over HTTPS (in May 2018 according to this) and so, having already moved web hosts once due to wildly inconsistent performance from the first provider, I decided to use this to-static-site logic and start publishing via GitHub Pages.
This is a long-winded way of saying that, although I publish my content these days as a static site, I write new content by running the original blog app locally and then turning it into static content later. Meaning that the original individual post files are available in the ASP.NET MVC Blog GitHub repo here:
github.com/ProductiveRage/Blog/tree/master/Blog/App_Data/Posts
Therefore, if you were sufficiently curious and wanted to play along at home, you can also access the original markdown files for my blog posts and see if you can reproduce my results.
Following shortly is some code to do just that. GitHub has an API that allows you to query folder contents and so we can get a list of blog post files without having to do anything arduous like clone the entire repo or trying to scrape the information from the site or even creating an authenticated API access application because GitHub allows us rate-limited non-authenticated access for free! Once we have the list of files, each will have a "download_url" that we can retrieve the raw content from.
To get the list of blog post files, you would call:
api.github.com/repos/ProductiveRage/Blog/contents/Blog/App_Data/Posts?ref=master
.. and get results that look like this:
[
{
"name": "1,2011,3,14,20,14,2,0,Immutability.txt",
"path": "Blog/App_Data/Posts/1,2011,3,14,20,14,2,0,Immutability.txt",
"sha": "b243ea15c891f73550485af27fa06dd1ccb8bf45",
"size": 18965,
"url": "https://api.github.com/repos/ProductiveRage/Blog/contents/Blog/App_Data/Posts/1,2011,3,14,20,14,2,0,Immutability.txt?ref=master",
"html_url": "https://github.com/ProductiveRage/Blog/blob/master/Blog/App_Data/Posts/1,2011,3,14,20,14,2,0,Immutability.txt",
"git_url": "https://api.github.com/repos/ProductiveRage/Blog/git/blobs/b243ea15c891f73550485af27fa06dd1ccb8bf45",
"download_url": "https://raw.githubusercontent.com/ProductiveRage/Blog/master/Blog/App_Data/Posts/1%2C2011%2C3%2C14%2C20%2C14%2C2%2C0%2CImmutability.txt",
"type": "file",
"_links": {
"self": "https://api.github.com/repos/ProductiveRage/Blog/contents/Blog/App_Data/Posts/1,2011,3,14,20,14,2,0,Immutability.txt?ref=master",
"git": "https://api.github.com/repos/ProductiveRage/Blog/git/blobs/b243ea15c891f73550485af27fa06dd1ccb8bf45",
"html": "https://github.com/ProductiveRage/Blog/blob/master/Blog/App_Data/Posts/1,2011,3,14,20,14,2,0,Immutability.txt"
}
},
{
"name": "10,2011,8,30,19,06,0,0,Mercurial.txt",
"path": "Blog/App_Data/Posts/10,2011,8,30,19,06,0,0,Mercurial.txt",
"sha": "ab6cf2fc360948212e29c64d9c886b3dbfe0d6fc",
"size": 3600,
"url": "https://api.github.com/repos/ProductiveRage/Blog/contents/Blog/App_Data/Posts/10,2011,8,30,19,06,0,0,Mercurial.txt?ref=master",
"html_url": "https://github.com/ProductiveRage/Blog/blob/master/Blog/App_Data/Posts/10,2011,8,30,19,06,0,0,Mercurial.txt",
"git_url": "https://api.github.com/repos/ProductiveRage/Blog/git/blobs/ab6cf2fc360948212e29c64d9c886b3dbfe0d6fc",
"download_url": "https://raw.githubusercontent.com/ProductiveRage/Blog/master/Blog/App_Data/Posts/10%2C2011%2C8%2C30%2C19%2C06%2C0%2C0%2CMercurial.txt",
"type": "file",
"_links": {
"self": "https://api.github.com/repos/ProductiveRage/Blog/contents/Blog/App_Data/Posts/10,2011,8,30,19,06,0,0,Mercurial.txt?ref=master",
"git": "https://api.github.com/repos/ProductiveRage/Blog/git/blobs/ab6cf2fc360948212e29c64d9c886b3dbfe0d6fc",
"html": "https://github.com/ProductiveRage/Blog/blob/master/Blog/App_Data/Posts/10,2011,8,30,19,06,0,0,Mercurial.txt"
}
},
..
While the API is rate-limited, retrieving content via the "download_url" locations is not - so we can make a single API call for the list and then download all of the individual files that we want.
Note that there are a couple of files in that folders that are NOT blog posts (such as the "RelatedPosts.txt" file, which is the way that I manually associate "You may also be interested in" post) and so each filename will have to be checked to ensure that it matches the format shown above.
The title of the blog post is not in the file name, it is always the first line of the content in the file (to obtain it, we'll need to process the file as markdown content, convert it to plain text and then look at that first line).
private static async Task<IEnumerable<BlogPost>> GetBlogPosts()
{
// Note: The GitHub API is rate limited quite severely for non-authenticated apps, so we just
// call it once for the list of files and then retrieve them all further down via the Download
// URLs (which don't count as API calls). Still, if you run this code repeatedly and start
// getting 403 "rate limited" responses then you might have to hold off for a while.
string namesAndUrlsJson;
using (var client = new WebClient())
{
// The API refuses requests without a User Agent, so set one before calling (see
// https://docs.github.com/en/rest/overview/resources-in-the-rest-api#user-agent-required)
client.Headers.Add(HttpRequestHeader.UserAgent, "ProductiveRage Blog Post Example");
namesAndUrlsJson = await client.DownloadStringTaskAsync(new Uri(
"https://api.github.com/repos/ProductiveRage/Blog/contents/Blog/App_Data/Posts?ref=master"
));
}
// Deserialise the response into an array of entries that have Name and Download_Url properties
var namesAndUrls = JsonConvert.DeserializeAnonymousType(
namesAndUrlsJson,
new[] { new { Name = "", Download_Url = (Uri)null } }
);
return await Task.WhenAll(namesAndUrls
.Select(entry =>
{
var fileNameSegments = Path.GetFileNameWithoutExtension(entry.Name).Split(",");
if (fileNameSegments.Length < 8)
return default;
if (!int.TryParse(fileNameSegments[0], out var id))
return default;
var dateContent = string.Join(",", fileNameSegments.Skip(1).Take(6));
if (!DateTime.TryParseExact(dateContent, "yyyy,M,d,H,m,s", default, default, out var date))
return default;
return (PostID: id, PublishedAt: date, entry.Download_Url);
})
.Where(entry => entry != default)
.Select(async entry =>
{
// Read the file content as markdown and parse into plain text (the first line of which
// will be the title of the post)
string markdown;
using (var client = new WebClient())
{
markdown = await client.DownloadStringTaskAsync(entry.Download_Url);
}
var plainText = Markdown.ToPlainText(markdown);
var title = plainText.Replace("\r\n", "\n").Replace('\r', '\n').Split('\n').First();
return new BlogPost(entry.PostID, title, plainText, entry.PublishedAt);
})
);
}
private sealed class BlogPost
{
public BlogPost(int id, string title, string plainTextContent, DateTime publishedAt)
{
ID = id;
Title = !string.IsNullOrWhiteSpace(title)
? title
: throw new ArgumentException("may not be null, blank or whitespace-only");
PlainTextContent = !string.IsNullOrWhiteSpace(plainTextContent)
? plainTextContent
: throw new ArgumentException("may not be null, blank or whitespace-only");
PublishedAt = publishedAt;
}
public int ID{ get; }
public string Title { get; }
public string PlainTextContent { get; }
public DateTime PublishedAt { get; }
}
(Note: I use the Markdig library to process markdown)
Training a FastText model
This raw blog post content needs to transformed into Catalyst "documents", then tokenised (split into individual sentences and words), then fed into a FastText model trainer.
Before getting to the code, I want to discuss a couple of oddities coming up. Firstly, Catalyst documents are required to train the FastText model and each document instance must be uniquely identified by a UID128 value, which is fine because we can generate them from the Title text of each blog post using the "Hash128()" extension method in Catalyst. However, (as we'll see a bit further down), when you ask for vectors* from the FastText model for the processed documents, each vector comes with a "Token" string that is the ID of the source document - so that has to be parsed back into a UID128. I'm not quite sure why the "Token" value isn't also a UID128 but it's no massive deal.
* (Vectors are just 1D arrays of floating point values - the FastText algorithm does magic to produce vectors that represent the text of the documents such that the distance between them can be compared; the length of these arrays is determined by the "Dimensions" option shown below and shorter distances between vectors suggest more similar content)
Next, there are the FastText settings that I've used. The Catalyst README has some code near the bottom for training a FastText embedding model but I didn't have much luck with the default options. Firstly, when I used the "FastText.ModelType.CBow" option then I didn't get any vectors generated and so I tried changing it to "FastText.ModelType.PVDM" and things started looked promising. Then I fiddled with some of the other settings. Some of which I have a rough idea what they mean and some, erm.. not so much.
The settings that I ended up using are these:
var fastText = new FastText(language, version: 0, tag: "");
fastText.Data.Type = FastText.ModelType.PVDM;
fastText.Data.Loss = FastText.LossType.NegativeSampling;
fastText.Data.IgnoreCase = true;
fastText.Data.Epoch = 50;
fastText.Data.Dimensions = 512;
fastText.Data.MinimumCount = 1;
fastText.Data.ContextWindow = 10;
fastText.Data.NegativeSamplingCount = 20;
I already mentioned changing the Data.Type / ModelType and the LossType ("NegativeSampling") is the value shown in the README. Then I felt like an obvious one to change was IgnoreCase, since that defaults to false and I think that I want it to be true - I don't care about the casing in any words when it's parsing my posts' content.
Now the others.. well, this library is built to work with systems with 10s or 100s of 1,000s of documents and that is a LOT more data than I have (currently around 120 blog posts) and so I made a few tweaks based on that. The "Epoch" count is the number of iterations that the training process will go through when constructing its model - by default, this is only 5 but I have limited data (meaning there's less for it to learn from but also that it's faster to complete each iteration) and so I bumped that up to 50. Then "Dimensions" is the size of the vectors generated - again, I figured that with limited data I would want a higher value and so I picked 512 (a nice round number if you're geeky enough) over the default 200. The "MinimumCount", I believe, relates to how often a word may appear and it defaults to 5 so I pulled it down to 1. The "ContextWindow" is (again, I think) how far to either side of any word that the process will look at in order to determine context - the larger the value, the more expensive the calculation; I bumped this from the default 5 up to 10. Then there's the "NegativeSamplingCount" value.. I have to just put my hands up and say that I have no idea what that actually does, only that I seemed to be getting better results with a value of 20 than I was with the default of 10.
With machine learning, there is almost always going to be some value to tweaking options (the "hyperparameters", if we're being all fancy) like this when building a model. Depending upon the model and the library, the defaults can be good for the general case but my tiny data set is not really what this library was intended for. Of course, machine learning experts have more idea what they're tweaking and (sometimes, at least) hopefully what results they'll get.. but I'm happy enough with where I've ended up with these.
This talk about what those machine learning experts do brings me on to the final thing that I wanted to talk about before showing the code; a little pre-processing / data-massaging. The better the data is that goes in, generally the better the results that come out will be. So another less glamorous part of the life of a Data Scientist is cleaning up data for training models.
In my case, that only extended to noticing that a few terms didn't seem to be getting recognised as essentially being the same thing and so I wanted to give it a little hand - for example, a fair number of my posts are about my "Full Text Indexer" project and so it probably makes sense to replace any instances of that string with a single concatenated word "FullTextIndexer". And I have a range of posts about React but I didn't want it to get confused with the verb "react" and so I replaced any "React" occurrence with "ReactJS" (now, this probably means that some "React" verb occurrences were incorrectly changed but I made the replacements of this word in a case-sensitive manner and felt like I would have likely used it as the noun more often than a verb with a capital letter due to the nature of my posts).
So I have a method to tidy up the plain text content a little:
private static string NormaliseSomeCommonTerms(string text) => text
.Replace(".NET", "NET", StringComparison.OrdinalIgnoreCase)
.Replace("Full Text Indexer", "FullTextIndexer", StringComparison.OrdinalIgnoreCase)
.Replace("Bridge.net", "BridgeNET", StringComparison.OrdinalIgnoreCase)
.Replace("React", "ReactJS");
Now let's get training!
Console.WriteLine("Reading posts from GitHub repo..");
var posts = await GetBlogPosts();
Console.WriteLine("Parsing documents..");
Storage.Current = new OnlineRepositoryStorage(new DiskStorage("catalyst-models"));
var language = Language.English;
var pipeline = Pipeline.For(language);
var postsWithDocuments = posts
.Select(post =>
{
var document = new Document(NormaliseSomeCommonTerms(post.PlainTextContent), language)
{
UID = post.Title.Hash128()
};
pipeline.ProcessSingle(document);
return (Post: post, Document: document);
})
.ToArray(); // Call ToArray to force evaluation of the document processing now
Console.WriteLine("Training FastText model..");
var fastText = new FastText(language, version: 0, tag: "");
fastText.Data.Type = FastText.ModelType.PVDM;
fastText.Data.Loss = FastText.LossType.NegativeSampling;
fastText.Data.IgnoreCase = true;
fastText.Data.Epoch = 50;
fastText.Data.Dimensions = 512;
fastText.Data.MinimumCount = 1;
fastText.Data.ContextWindow = 10;
fastText.Data.NegativeSamplingCount = 20;
fastText.Train(
postsWithDocuments.Select(postWithDocument => postWithDocument.Document),
trainingStatus: update => Console.WriteLine($" Progress: {update.Progress}, Epoch: {update.Epoch}")
);
Identifying similar documents using the model
Now that a model has been built that can represent all of my blog posts as vectors, we need to go through those post / vector combinations and identify others that are similar to it.
This will be achieved by using the HNSW.NET NuGet package that enables K-Nearest Neighbour (k-NN) searches over "high-dimensional space"*.
* (This just means that the vectors are relatively large; 512 in this case - two dimensions would be a point on a flat plane, three dimensions would be a physical point in space, anything with more dimensions that that is in "higher-dimensional space".. though that's not to say that any more than three dimensions is definitely a bad fit for a regular k-NN search but 512 dimensions IS going to be a bad fit and the HNSW approach will be much more efficient)
There are useful examples on the README about "How to build a graph?" and "How to run k-NN search?" and tweaking those for the data that I have so far leads to this:
Console.WriteLine("Building recommendations..");
// Combine the blog post data with the FastText-generated vectors
var results = fastText
.GetDocumentVectors()
.Select(result =>
{
// Each document vector instance will include a "token" string that may be mapped back to the
// UID of the document for each blog post. If there were a large number of posts to deal with
// then a dictionary to match UIDs to blog posts would be sensible for performance but I only
// have a 100+ and so a LINQ "First" scan over the list will suffice.
var uid = UID128.Parse(result.Token);
var postForResult = postsWithDocuments.First(
postWithDocument => postWithDocument.Document.UID == uid
);
return (UID: uid, result.Vector, postForResult.Post);
})
.ToArray(); // ToArray since we enumerate multiple times below
// Construct a graph to search over, as described at
// https://github.com/curiosity-ai/hnsw-sharp#how-to-build-a-graph
var graph = new SmallWorld<(UID128 UID, float[] Vector, BlogPost Post), float>(
distance: (to, from) => CosineDistance.NonOptimized(from.Vector, to.Vector),
DefaultRandomGenerator.Instance,
new() { M = 15, LevelLambda = 1 / Math.Log(15) }
);
graph.AddItems(results);
// For every post, use the "KNNSearch" method on the graph to find the three most similar posts
const int maximumNumberOfResultsToReturn = 3;
var postsWithSimilarResults = results
.Select(result =>
{
// Request one result too many from the KNNSearch call because it's expected that the original
// post will come back as the best match and we'll want to exclude that
var similarResults = graph
.KNNSearch(result, maximumNumberOfResultsToReturn + 1)
.Where(similarResult => similarResult.Item.UID != result.UID)
.Take(maximumNumberOfResultsToReturn); // Just in case the original post wasn't included
return new
{
result.Post,
Similar = similarResults
.Select(similarResult => new
{
similarResult.Id,
similarResult.Item.Post,
similarResult.Distance
})
.ToArray()
};
})
.OrderBy(result => result.Post.Title, StringComparer.OrdinalIgnoreCase)
.ToArray();
And with that, there is a list of every post from my blog and a list of the three blog posts most similar to it!
Well, "most similar" according to the model that we trained and the hyperparameters that we used to do so. As with many machine learning algorithms, it will have started from a random state and tweaked and tweaked until it's time for it to stop (based upon the "Epoch" value in this FastText case) and so the results each time may be a little different.
However, if we inspect the results like this:
foreach (var postWithSimilarResults in postsWithSimilarResults)
{
Console.WriteLine();
Console.WriteLine(postWithSimilarResults.Post.Title);
foreach (var similarResult in postWithSimilarResults.Similar.OrderBy(other => other.Distance))
Console.WriteLine($"{similarResult.Distance:0.000} {similarResult.Post.Title}");
}
.. then there are some good results to be found! Like these:
Learning F# via some Machine Learning: The Single Layer Perceptron
0.229 How are barcodes read?? (Library-less image processing in C#)
0.236 Writing F# to implement 'The Single Layer Perceptron'
0.299 Face or no face (finding faces in photos using C# and AccordNET)Translating VBScript into C#
0.257 VBScript is DIM
0.371 If you can keep your head when all about you are losing theirs and blaming it on VBScript
0.384 Using Roslyn to identify unused and undeclared variables in VBScript WSC componentsWriting React components in TypeScript
0.376 TypeScript classes for (React) Flux actions
0.378 React and Flux with DuoCode
0.410 React (and Flux) with Bridge.net
However, there are also some less good ones - like these:
A static type system is a wonderful message to the present and future
0.271 STA ApartmentState with ASP.Net MVC
0.291 CSS Minification Regular Expressions
0.303 Publishing RSSSimple TypeScript type definitions for AMD modules
0.162 STA ApartmentState with ASP.Net MVC
0.189 WCF with JSON (and nullable types)
0.191 The joys of AutoMapperSupporting IDispatch through the COMInteraction wrapper
0.394 A static type system is a wonderful message to the present and future
0.411 TypeScript State Machines
0.414 Simple TypeScript type definitions for AMD modules
Improving the results
I'd like to get this good enough that I can include auto-generated recommendations on my blog and I don't feel like the consistency in quality is there yet. If they were all like the good examples then I'd be ploughing ahead right now with enabling it! But there are mediocre examples as well as those poorer ones above.
It's quite possible that I could get closer by experimenting with the hyperparameters more but that does tend to get tedious when you have to analyse the output of each run manually - looking through all the 120-ish post titles and deciding whether the supposed best matches are good or not. It would be lovely if I could concoct some sort of metric of "goodness" and then have the computer try lots of variations of parameters but one of the downsides of having relatively little data is that that is difficult*.
* (On the flip side, if I had 1,000s of blog posts as source data then the difficult part would be manually labelling enough of them as "quite similar" in numbers sufficient for the computer to know if it's done better or done worse with each experiment)
Fortunately, I have another trick up my sleeve - but I'm going to leave that for next time! This post is already more than long enough, I think. The plan is to combine results from another model in the Catalyst with the FastText results and see if I can encourage things to look a bit neater.
Trying the code if you're lazy
If you want to try fiddling with this code but don't want to copy-paste the sections above into a new project, you can find the complete sample in the "Similarity" project in the solution of this repo: BlogPostSimilarity.
Posted at 22:21
Language detection and words-in-sentence classification in C#
TL;(BG)DR
Using an open source .NET library, it's easy to determine what language a sentence / paragraph / document is written in and to then classify the words in each sentence into verbs, nouns, etc..
What library?
I recently parted ways on very good terms with my last employers (and friends!) at Curiosity AI but that doesn't mean that I'm not still excited by their technology, some really useful aspects of which they have released as open source*.
* (For the full service, ask yourself if your team or your company have ever struggled to find some information that you know exists somewhere but that might be in one of your network drives containing 10s of 1,000s of files or in your emails or in Sharepoint or GDrive somewhere - with Curiosity, you can set up a system that will index all that data so that it's searchable in one place, as well as learning synonyms and abbreviations in case you can't conjure up the precise terms to search for. It can even find similar documents for those case where have one document to hand and just know that there's another related to it but are struggling to find it - plus it has an ingrained permissions model so that your team could all index their emails and GDrive files and be secure in the knowledge that only they and people that they've shared the files with can see them; they don't get pulled in in such a way that your private, intimate, confidential emails are now visible to everyone!)
I have a little time off between jobs and so I wanted to write a little bit about some of the open-sourced projects that they released that I think are cool.
This first one is a really simple example but I think that it demonstrates how easily you can access capabilities that are pretty impressive.
This is my cat Cass:

She looks so cute that you'd think butter wouldn't melt. But, of my three cats, she is the prime suspect for the pigeon carcus that was recently dragged through the cat flap one night, up a flight of stairs and deposited outside my home office - and, perhaps not coincidentally, a mere six feet away from where she'd recently made herself a cosy bed in a duvet cover that I'd left out to remind myself to wash.
I think that it's a fair conclusion to draw that:
My cat Cass is a lovely fluffy little pigeon-killer!
Now you and I can easily see that that is a sentence written in English. But if you wanted a computer to work it out, how would you go about it?
Well, one way would be to install the Catalyst NuGet package and write the following code:
using System;
using System.IO;
using System.Threading.Tasks;
using Catalyst;
using Catalyst.Models;
using Mosaik.Core;
using Version = Mosaik.Core.Version;
namespace CatalystExamples
{
internal static class Program
{
private static async Task Main()
{
const string text = "My cat Cass is a lovely fluffy little pigeon-killer!";
Console.WriteLine("Downloading/reading language detection models..");
const string modelFolderName = "catalyst-models";
if (!new DirectoryInfo(modelFolderName).Exists)
Console.WriteLine("- Downloading for the first time, so this may take a little while");
Storage.Current = new OnlineRepositoryStorage(new DiskStorage(modelFolderName));
var languageDetector = await FastTextLanguageDetector.FromStoreAsync(
Language.Any,
Version.Latest,
""
);
Console.WriteLine();
var doc = new Document(text);
languageDetector.Process(doc);
Console.WriteLine(text);
Console.WriteLine($"Detected language: {doc.Language}");
}
}
}
Running this code will print the following to the console:
Downloading/reading language detection models..
- Downloading for the first time, so this may take a little while
My cat Cass is a lovely fluffy little pigeon-killer!
Detected language: English
Just to prove that it doesn't only detect English, I ran the sentence through Google Translate to get a German version (unfortunately, the languages I'm fluent in are only English and a few computer languages and so Google Translate was very much needed!) - thus changing the "text" definition to:
const string text = "Meine Katze Cass ist eine schöne flauschige kleine Taubenmörderin!";
Running the altered program results in the following console output:
Downloading/reading language detection models..
Meine Katze Cass ist eine wunderschöne, flauschige kleine Taubenmörderin!
Detected language: German
Great success!
The next thing that we can do is analyse the grammatical constructs of the sentence. I'm going to return to the English version for this because it will be easier for me to be confident that the word classifications are correct.
Add the following code immediately after the Console.WriteLine calls in the Main method from earlier:
Console.WriteLine();
Console.WriteLine($"Downloading/reading part-of-speech model for {doc.Language}..");
var pipeline = await Pipeline.ForAsync(doc.Language);
pipeline.ProcessSingle(doc);
foreach (var sentence in doc)
{
foreach (var token in sentence)
Console.WriteLine($"{token.Value}{new string(' ', 20 - token.Value.Length)}{token.POS}");
}
The program will now write the following to the console:
Downloading/reading language detection models..
My cat Cass is a lovely fluffy little pigeon-killer!
Detected language: English
Downloading/reading part-of-speech model for English..
My PRON
cat NOUN
Cass PROPN
is AUX
a DET
lovely ADJ
fluffy ADJ
little ADJ
pigeon-killer NOUN
! PUNCT
The "Part of Speech" (PoS) categories shown above are (as quoted from universaldependencies.org/u/pos/all.html) -
| Word(s) | Code | Name | Description |
|---|---|---|---|
| My | PRON | Pronoun | words that substitute for nouns or noun phrases, whose meaning is recoverable from the linguistic or extralinguistic context |
| cat, pigeon-killer | NOUN | Noun | a part of speech typically denoting a person, place, thing, animal or idea |
| Cass | PNOUN | Proper Noun | a noun (or nominal content word) that is the name (or part of the name) of a specific individual, place, or object |
| is | AUX | Auxillary Verb | a function word that accompanies the lexical verb of a verb phrase and expresses grammatical distinctions not carried by the lexical verb, such as person, number, tense, mood, aspect, voice or evidentiality |
| a | DET | Determiner | words that modify nouns or noun phrases and express the reference of the noun phrase in context |
| lovely, fluffy, little | ADJ | Adjective | words that typically modify nouns and specify their properties or attributes |
| ! | PUNCT | Punctuation | non-alphabetical characters and character groups used in many languages to delimit linguistic units in printed text |
How easy was that?! There are a myriad of uses for this sort of analysis (one of the things that the full Curiosity system uses it for is identifying nouns throughout documents and creating tags that any documents sharing a given noun are linked via; so if you found one document about "Flux Capacitors" then you could easily identify all of the other documents / emails / memos that mentioned it - though that really is just the tip of the iceberg).
Very minor caveats
I have only a couple of warnings before signing off this post. I've seen the sentence detector get confused if it has very little data to work with (a tiny segment fragment, for example) or if there is a document that has different sections written in multiple languages - but I don't think that either case is unreasonable, the library is very clever but it can't perform magic!
Coming soon
I've got another post relating to their open-sourced libraries in the pipeline, hopefully I'll get that out this week! Let's just say that I'm hoping that my days of having to manually maintain the "you may also be interested" links between my posts will soon be behind me!
Posted at 19:52
Writing F# to implement 'The Single Layer Perceptron'
TL;DR
This picks up from my last post Learning F# via some Machine Learning: The Single Layer Perceptron where I described a simple neural network ("The Single Layer Perceptron") and took a C# implementation (from an article on the site Robosoup) and rewrote it into a style of "functional C#" with the intention of then translating it into F#. Trying to do that all in one post would have made for a very very long read and so part two, here, picks things up from that point.
I'm still an F# beginner and so I'm hoping that having the pain so fresh in my mind of trying to pick it up as a new language will make it easier for me to help others get started. I'm going to assume zero knowledge from the reader.
(I'm also going to try to dive straight right into things, rather than covering loads of theory first - I think that there are a lot of good resources out there that introduce you to F# and functional concepts at a more abstract level but I'm going to take the approach that we want to tackle something specific and we'll discuss new F# concepts only when we encounter them while trying to get this work done!)
Translating the code into F#
Visual Studio 2017 includes support for F# without having to install anything extra. To get started, create a new project of type Visual F# / Console Application. This will generate a Program.fs file that will let you build and run (it won't be anything very interesting if you run it but that doesn't matter because we're going rewrite the file from scratch!).
In the C# code from last time, the core logic was contained within a static method called "Go" within a static class. To set up the scaffolding for something similar in F# we'll use the following code:
open System;
let private Go (r: Random) =
"TODO: Implement this"
[<EntryPoint>]
let private Main _ =
Go (new Random(0)) |> ignore
0
In F#, functions are declared by the keyword "let" optionally followed by an accessibility modifier (eg. "private") followed by their name followed by their arguments followed by "=" followed by the function body.
The last line of the function body will be a value that is returned by the function (unlike C#, there is no need for an explicit "return" keyword).
Above, there is a function "Go" that takes a Random argument named "r" and that returns a string. The return type is not explicitly declared anywhere but F# relies upon type inference a lot of the time to make reduce the "syntactic noise" around declaring types where the compiler can work them out on its own. If you wanted reassurance that the type inference has worked as you expect then you can hover over the word "Go" and you'll see the following signature for the function -
val private Go : r:Random -> string
This confirms that the function "Go" takes an argument named "r" of type random and that it returns a string.
If we changed the "Go" function to this:
let private Go r =
"TODO: Implement this"
.. and then hovered over the word "Go" then we'd see the following signature:
val private Go : r:'a -> string
This essentially means that the type "r" is not fixed and that it may be any type because there is no way for the compiler to apply any restrictions to it based upon the code that it has access to. When comparing to C#, you might imagine that this would be equivalent to this:
private string Go(object r)
.. but it would actually be more accurate to think about it like a generic method - eg.
private string Go<T>(T r)
The difference isn't important right now it's worth bearing in mind.
There's also a function "Main" that takes a single string argument argument named "_" and that returns an int. Just looking at this code, you may imagine that "_" would also be of an unknown / generic type but if you hover to the word "Main" then you'll see this signature:
val private main : string [] -> int
F# has applied some extra logic here, based upon the fact that the function has been annotated with [<EntryPoint>] - this requires that the function matches the particular signature of string-array-to-string and you will get a compile error if you try to declare a function signature that differs from this.
The string array is a list of arguments passed to the compiled executable if called from the command line. This will never be of use in this program and so I've named that argument "_" to tell F# that I will never want to access it. I do this because F# will warn you if you have any unused arguments because it suggests that you have forgotten something (why specify an argument if you don't need it??). If you really don't care about one, though (as is the case here), if you give it an underscore prefix (or call it simply "_") then the compiler won't warn you about it.
In a similar vein, F# will warn you if you call a function and ignore its return value. If the idea is that all functions be pure (and so have no side effects) then a function is useless if you ignore its return value. In the scaffolding above, though, we just want to call "Go" (which will do some calculations and write a summary to the console) - we don't really care about its return value. To tell the compiler this, we use a special function called "ignore" that we pass the return value of the "Go" function to. The C# way to do this might look something like this:
ignore(Go(new Random(0)))
This is valid F# but it's criticised as having to be read "inside out". It's more common in F# to see it like this:
Go (new Random(0)) |> ignore
The "pipe forward" operator (|>) effectively means take the value on the left and use it as the last argument in the function on the right. Since "ignore" only takes one argument, the two versions above are equivalent.
If a function has more than one argument then the pipe operator only provides the last one. To illustrate this, consider the method "List.map" that takes two arguments; a "mapping" delegate and a list of items. It's very similar to LINQ's "Select" method. You could call it like this:
let numbers = [1;2;3]
let squares = List.map (fun x -> x * x) numbers
I'll breeze through some of the syntax above in a moment but the important point here is that there is a method that takes two arguments where the second is a list.
It could be argued that this syntax is back-to-front because you may describe this in English as:
given a list of values, perform an operation on each item (and return a new list containing the transformed - or "mapped" - values)
.. but the code puts things in the opposite order ("list of values" is mentioned last instead of first).
However, the pipe operator changes that -
let numbers = [1;2;3]
let squares = numbers |> List.map (fun x -> x * x)
The code now is able to say "here is the list, perform this operation on each value to provide me with a new list".
Because the pipe operator passes the value on the left as the last argument to the function on the right, F# often has list-based functions where the list is the last argument. This is often the opposite order to C# functions, where the "subject" of the operation is the commonly first argument.
Now, as promised, a quick rundown of F# syntax introduced above. The "let" keyword is very similar to C#'s "var" in that it use type inference to determine what type the specific reference should be. Unlike "var", though, you can't change the reference later on - eg.
let numbers = [1;2;3]
// Invalid! This "=" operator is treated as a comparison whose return value is ignored
// rather than this statement being a reassignment - the "numbers" reference is still
// a list with the values 1, 2 and 3 (a compiler warning will be displayed)
numbers = [1;2;3;4]
Because F# only allows you to set value in statements that include the "let" operator, it makes it easier for the F# compiler to know whether the code fragment:
a = b
is an assignment or a comparison - if it follows a "let" then it's always an assignment but otherwise it's a comparison.
This is unlike C# where the following is acceptable:
var numbers = new[] { 1, 2, 3 };
// This is allowed in C#
numbers = new[] { 1, 2, 3, 4 };
.. and this means that the C# compiler can't as easily tell whether the code fragment "a = b" is an assignment or a comparison and that is why C# has the assignment operator "=" and a separate equality comparison operator "==" (and why F# can use "=" as both the assignment operator and equality comparison operator).
The next thing to talk about is that F# allows you to declare a list of values using square brackets and semi-colons as the separators. So the below are similar (but not equivalent, as I'll explain) in C#
and F# -
var numbers = new List<int> { 1, 2, 3 }; // C#
let numbers = [1;2;3] // F#
The reason that they're similar and not identical is that the C# code uses the System.Collections.Generic.List<T> type, which is mutable (you can add, remove and replace items within a list). In F#, the list is immutable and so any operation (such as add, remove or replace) would return a new list reference, rather than mutating the existing list.
You may have noticed that semi-colons are not present at the end of each F# line in the examples above. That's because they are not required. F# uses whitespace (such as line returns and indenting) to determine when statements terminate and when they continue and so semi-colons are not used to specify where statements finish (unlike in C#, where they are).
Finally, there was a delegate shown in the above code -
(fun x -> x * x)
This is an anonymous function. The F# code:
let numbers = [1;2;3]
let squares = numbers |> List.map (fun x -> x * x)
is roughly the same as the following C# code:
var numbers = new[] { 1, 2, 3 };
var squares = numbers.Select(x => x * x);
It's not precisely the same since "numbers" in the F# code is an immutable list reference and in C# it's an array but it's close enough. The point is that the "fun" keyword is used to declare an anonymous function and that brackets are required around that function declaration in order to segregate that code and make it clear to the compiler that the function declaration should be considered as a single value that is being passed to the "List.map" function.
Declaring training data
In the C# perceptron code from last week, there was an array of Tuple values that contained each pair of inputs and the expected result -
var trainingData = new[]
{
Pattern(0.08, 0.94, true),
// .. more patterns
};
The "Pattern" function was just this:
private static Tuple<double[], bool> Pattern(double x, double y, bool output)
{
return Tuple.Create(new[] { x, y }, output);
}
The Tuple class is a very convenient way to represent small groups of values (such as an input array and the expected boolean output) but one thing that I don't like is that the properties are named "Item1", "Item2", etc.. rather than it being possible to give them more descriptive labels.
I could have defined a class to contain these values but that can involve a lot of boilerplate code (particularly if it's an immutable class, which would be my preference when creating classes that describe data that should be initialised once and never changed).
Fortunately, F# has a convenient way to describe data like this called "Records" - immutable types that may be defined using very little syntax, such as by pasting the following into the F# scaffolding from earlier, just after "Open System" -
type private Input = { Values: float list; Result: bool }
It is now possible to define an input list / output boolean object with properties name "Values" and "Result" like this:
let x = { Values = [0.08; 0.94]; Result = true }
The type of "x" is not explicitly specified in the code but the compiler will be able to match it to the Input type.
double vs float
Note that I've defined the "Values" property to be of type "float list" (which is equivalent to "list<float>" - which is also valid syntax in F#) as opposed to "double list". In C#, Double and double represent a "double-precision floating point number" while Single and float represent a "single-precision floating point number". In F#, float is a double-precision floating point number while float32 is a single-precision floating point number. So "float" in F# is the same as "double" in C#. To make things more confusing, you can also specify the type double in F# and it means the same as float in F# - however, type signatures in the F# library specify float when a double-precision floating point number is returned and so I'm specifying float to try to be consistent with other F# code. For example, the library function "Double.Parse" returns float according to intellisense.
This seems quite confusing to me (coming at this from C#) but I decided to try to be as F#-like as possible and so "float list" is what I'm using.
Back to declaring training data..
To declare all of the training data in F#, we want a list of patterns -
let trainingData = [
{ Values = [0.08; 0.94]; Result = true }
{ Values = [0.13; 0.95]; Result = true }
// .. more patterns
]
When declaring a list (items within square brackets), they may either be separated by semi-colons or by line returns. So, above, each pattern is on its own line and so no semi-colons need to separate them while the individual numbers within the "Values" lists do need semi-colon separators since there are no line returns to break them up.
In the C# code, the "Pattern" function specifically took two "x" and "y" arguments and so each Tuple had an "Item1" property which was an array with two elements. In the above code, there would be no compiler warning if I accidentally included a line where the pattern had more "Values" entries than the others. As a sanity check, we can include the following code after the "trainingData" list is declared -
let inputLengths =
trainingData
|> List.map (fun input -> input.Values.Length)
|> List.distinct
|> List.length
if (inputLengths > 1) then raise (Exception "Inconsistent pattern input lengths!")
There's a lot of piping here, which seems to be quite common in F# code. Hopefully, though, it illustrates how using the pipe operator allows code to be written in a more logical order. Here, we're saying:
- Take the trainingData list
- Construct a list where each entry in the new list corresponds to the number of inputs in a trainingData entry
- Build a new list from this by taking this list-of-input-lengths and excluding any duplicates
- If the list from step 3 has more than one entry then the trainingData must not have entries that all have the same number of inputs
If the "trainingData" has patterns which all have the same number of inputs then there should only be one unique input input-list-length. If some patterns had two inputs and some patterns had three inputs then we would get more than one unique input-list-length and that would not be good.
Since F# has a concept of "significant whitespace" (meaning that it uses line returns and indentation to indicate where expressions start and end, which is why semi-colons are not required to terminate lines), sometimes it can get a bit demanding about what it thinks it ok and what isn't. In the code above, if you tried to put the "trainingData" on the same line as the "let inputLengths =" and then have the pipe operator lines start underneath it then you will get cryptic errors such as "The block following this 'let' is unfinished". Using the format above not only means that your code will be more consistent with other F# "in the wild" but it also means that the compiler will understand it!
// The F# compiler is happy with this..
let inputLengths =
trainingData
|> List.map (fun input -> input.Values.Length)
|> List.distinct
|> List.length
// .. it is NOT happy with this..
let inputLengths = trainingData
|> List.map (fun input -> input.Values.Length)
|> List.distinct
|> List.length
(I would not have thought that putting "trainingData" on the same line as "let inputLengths =" would introduce any ambiguity but presumably doing similar things must do in some situations).
Translating the network-training code
The c# code that we ended up with last time for training a network looked like this:
const double learningRate = 0.1;
var finalResult = Enumerable.Range(0, int.MaxValue)
.Scan(
seed: new
{
Weights = new[] { r.NextDouble(), r.NextDouble() },
Bias = 0d,
GlobalError = double.MaxValue
},
func: (previousState, iteration) =>
{
var resultForIteration = trainingData.Aggregate(
seed: new { Weights = previousState.Weights, Bias = previousState.Bias, GlobalError = 0d },
func: (stateSoFar, pattern) =>
{
var output = Output(stateSoFar.Weights, stateSoFar.Bias, pattern.Item1) ? 1 : -1;
var localError = (pattern.Item2 ? 1 : -1) - output;
return new
{
Weights = UpdateWeights(stateSoFar.Weights, learningRate, localError, pattern.Item1),
Bias = stateSoFar.Bias + (learningRate * localError),
GlobalError = stateSoFar.GlobalError + Math.Abs(localError)
};
}
);
Console.WriteLine("Iteration {0}\tError {1}", iteration, resultForIteration.GlobalError);
return resultForIteration;
}
)
.First(state => state.GlobalError <= 0);
.. and relied upon the following two functions:
private static bool Output(double[] weights, double bias, double[] inputs)
{
var sum = inputs.Zip(weights, (input, weight) => input * weight).Sum() + bias;
return (sum >= 0);
}
private static double[] UpdateWeights(double[] weights, double learningRate, double localError, double[] inputs)
{
if (localError == 0)
return weights;
return weights
.Zip(inputs, (weight, input) => weight + (learningRate * localError * input))
.ToArray();
}
I'm going to start with translating the "Output" function first because it will be relatively straight forward but it will also demonstrate some interesting abilities of the F# compiler's type inference abilities.
Type inference means that there are a lot of types that you don't have to specify in F# code because the compiler will be able to work out what they are. But this can be confusing sometimes if you don't have a strong enough grasp on how the compiler does this.
Because I'm still an F# noob, I like to specify function arguments types to begin with and then remove them afterwards once I can see that the compiler is happy without them and when I understand how the compiler knows. So I'll start with this:
let Output (weights: float list) (bias: float) (inputs: float list) =
let sum = (List.zip weights inputs |> List.map (fun (weight, input) -> weight * input) |> List.sum) + bias
sum >= float 0
The brackets around the arguments are required to "group" the argument name and its type into one value. When we remove the type annotations shortly, the argument brackets will no longer be necessary.
The "List.zip" function is very similar to LINQ's "Zip" function except that it has no facility to take a delegate to combine the two values, instead it always returns a tuple for each pair of values that it combines.
(I didn't use the pipe operator with the "List.zip" call above because I think that it read more naturally without it in this case - I think of this as "zipping the weights and inputs lists together" and that is what the code says)
F# has nice support for tuples that allows us to avoid having to rely upon "Item1" and "Item2" accesses. The lambda above that performs multiplication would have to look something like this in C# if the input was a tuple:
weightAndInput => weightAndInput.Item1 * weightAndInput.Item2
.. but F# allows us to "deconstruct" the tuple by providing names for the tuple properties - ie.
fun (weight, input) -> weight * input
This is still a function that takes a single argument, it's just that that single argument is a two-item tuple and we're accessing its two items through named references "weight" and "input".
Hopefully the rest of the code is easy to understand, "List.zip" is like LINQ's "Zip" and "List.map" is like LINQ's "Select" and "List.sum" is like LINQ's "Sum".
The second line "sum >= float 0" is the return value for the function - either true or false. The expression "float 0" is important because the "sum" value will be a float and F# will not attempt any type coercion when comparing values. In C#, if you have two numeric types then you can compare them - eg.
// Valid in C#
double x1 = 0; // double
int x2 = 0; // int
var isMatch = (x1 == x2);
.. but in F# this is not allowed. If you tried to write the following:
// Not allowed in F#
let x1 = float 0 // float
let x2 = 0 // int
let isMatch = (x1 = x2)
.. then you would get the following error:
This expression was expected to have type 'float' but here has type 'int'
Now that we're happy with the function implementation, we can remove the type annotations and reduce it to this:
let Output weights bias inputs =
let sum = (List.zip weights inputs |> List.map (fun (weight, input) -> weight * input) |> List.sum) + bias
sum >= float 0
The compiler is able to infer all of those types. Some of the inference is quite simple - for example, both "weights" and "inputs" must be lists of some type because they are passed to "List.zip".
Some of the inference is more complicated, though..
Firstly, the "weights" and "inputs" list must have element types that support a "*" operator (in F#, this means any of the numeric types or any type that has got a custom "*" overload implemented on it).
Secondly, when elements are combined from "weight" and "inputs" using "*", it must be possible to use the "+" operator on the result because "List.sum" requires it (the internal implementation of "List.sum" is to combine all of the values passed to it using "+").
Thirdly, the result from "List.sum" must also support the "+" operator in conjunction with whatever type that "bias" is.
Fourthly, this result must support the ">=" operator in conjunction with "float 0".
Working backwards, because F# does not support any type coercion when comparing numeric values, the type of "sum" must be float in order for it to be compared to "float 0". This means that the result of "List.sum" must be float and so "bias" must be float. This means that the "weights" and "inputs" must be lists of float. (The return type of the function is boolean because the return value is always true or false as it is the result of an ">=" comparison).
This type inference is very powerful and can lead to clean and succint code. However, it can also lead to confusion if you haven't perfectly internalised its workings or if you're dealing with incomplete code. It's for both of those reasons that I prefer to start with more argument type annotations than necessary and then remove them later, when I'm happy with what I've written.
The "UpdateWeights" function may be translated in a similar manner -
let UpdateWeights weights localError inputs =
if (localError = float 0)
then weights
else
List.zip weights inputs
|> List.map (fun (weight, input) -> weight + (learningRate * localError * input))
In F#, if / then / else is a bit different to C#. In F#, it is an expression that returns a value, so you could write something like:
// Valid F#
let x = if something then 1 else 2
// Not valid C#
var x = if something then 1 else 2
So, in the F# "UpdateWeights" function, the "if" expression returns either the original "weights" reference or the updated list.
We've actually seen quite a lot of F# syntax, just in the code above - variable and function definitions, type annotations (and discussed how they are optional in many cases), anonymous functions (with the "fun" keyword), the pipe forward operator, record types, tuple deconstruction. Let's throw in another one; nested functions. The two functions shown above ("Output" and "UpdateWeights") will only be called from within the "Go" function that was part of the initial scaffolding code. We could make these private functions at the same level as "Go".. or we can make them nested functions within "Go" so that their scope is as restrictive as possible (which is a good thing in my book) -
let private Go (r: Random) =
let Output weights bias inputs =
let sum = (List.zip weights inputs |> List.map (fun (weight, input) -> weight * input) |> List.sum) + bias
sum >= float 0
let UpdateWeights weights localError inputs =
if (localError = float 0)
then weights
else
List.zip weights inputs
|> List.map (fun (weight, input) -> weight + (learningRate * localError * input))
"TODO: Implement this"
Sidebar: The influence of F# on C#
It seems that quite a lot of features from F# are coming over to C# from C# 7 onwards. For example, nested functions are already available (they weren't in C# 6 but they are in C# 7) - eg.
public static void Go()
{
int GetNumber()
{
return 123;
}
Console.WriteLine(GetNumber());
}
Similarly, Tuple deconstruction is also now available -
public static void Go()
{
var (inputs, output) = GetPattern();
Console.WriteLine(string.Join(", ", inputs));
Console.WriteLine(output);
}
// Note: We're not returning a "Tuple<double[], bool>" here, it's a different type (and it requires
// the "System.ValueType" package to be added to the project
private static (double[] inputs, bool output) GetPattern()
{
return (new[] { 0.5, 0.6 }, true);
}
Coming at some point (looks like it will be C# 8), there will be support for defining record types -
// This syntax is not yet available (as of January 2018)
public class Point(int X, int Y);
The Point class will have X and Y properties that are set through a constructor call. It will have an "Equals" implementation that will return true for two Point references that have the same X and Y values (and probably have == and != operator overloads that do the same thing) and it will have a "With" method that allows you to take an instance of a Point and create a new instance that has a new value for either X or Y - eg.
var p1 = new Point(1, 2);
var p2 = new Point(1, 2);
Console.WriteLine(p1 == p2); // True!
p2 = p2.With(X: 7);
Console.WriteLine(p1 == p2); // False
(For more details about C# record types, see the records proposal).
It's interesting to see these features working their way into C# and hopefully it will make it easier for someone in the future to try F# if they already know C#. (Some may argue that it could make F# less appealing with more of its features being added to C# but I think that it will still have enough differences to stand apart - having immutability and non-nulls by default is not something that is likely to be incorporated into C# because it would require enormous changes).
Back to translating the network-training code..
Now that the supporting functions ("Output" and "UpdateWeights") have been translated, we need to look back at the main training code. This time I'm going to go "outside in" and translate this:
const double learningRate = 0.1;
var finalResult = Enumerable.Range(0, int.MaxValue)
.Scan(
seed: new
{
Weights = new[] { r.NextDouble(), r.NextDouble() },
Bias = 0d,
GlobalError = double.MaxValue
},
func: (previousState, iteration) =>
{
// Do work here..
}
)
.First(state => state.GlobalError <= 0);
The "Enumerable.Range(0, int.MaxValue)" line was basically a way to say "keep enumerating for ever" (int.MaxValue isn't technically the same as "forever" but in this context it's good enough because we'll die of boredom waiting for the code to perform two billion iterations).
In F# there is a function that seems closer to what we want called "Seq.initInfinite" - this takes a single argument that is a delegate that takes an int and returns a value in the generated sequence based upon that int. It could be implemented in C# like this:
public static IEnumerable<T> InitInfinite<T>(Func<int, T> initialiser)
{
return Enumerable.Range(0, int.MaxValue).Select(initialiser);
}
This is also limited to int.MaxValue iterations since the delegate argument is an int but we're still not going to worry too much about whether it's really infinite or not.
From my last post, we know that "Scan" is already an F# concept and so that should be easy to translate.
The last function to translate is "First" and this has a corresponding function in F#; "Seq.find".
The only issue that we have to tackle now is that F# does not support anonymous types and so we'll need to declare another record type that I'll call "CalculationState".
type private CalculationState = {
Weights: List<float>
Bias: float
GlobalError: float
}
When I defined the "Input" record earlier, I used a single line definition and so each property had to be separated by semi-colons. Above, each property is on its line and so semi-colon delimiters are not required.
Now we can translate the above C# into this F#:
let finalResult =
Seq.initInfinite (fun i -> i)
|> Seq.scan
(fun previousState iteration ->
// Do work here..
)
{ Weights = [r.NextDouble(); r.NextDouble()]; Bias = float 0; GlobalError = Double.MaxValue }
|> Seq.find (fun state -> state.GlobalError = float 0)
The "// Do work here.." code looks like this in C# -
var resultForIteration = trainingData.Aggregate(
seed: new { Weights = previousState.Weights, Bias = previousState.Bias, GlobalError = 0d },
func: (stateSoFar, pattern) =>
{
var output = Output(stateSoFar.Weights, stateSoFar.Bias, pattern.Item1) ? 1 : -1;
var localError = (pattern.Item2 ? 1 : -1) - output;
return new
{
Weights = UpdateWeights(stateSoFar.Weights, learningRate, localError, pattern.Item1),
Bias = stateSoFar.Bias + (learningRate * localError),
GlobalError = stateSoFar.GlobalError + Math.Abs(localError)
};
}
);
Console.WriteLine("Iteration {0}\tError {1}", iteration, resultForIteration.GlobalError);
return resultForIteration;
I'm going to break this out into a separate function in the F# code because I want to avoid the final code being too "dense" (particularly while I'm still getting used to reading F# syntax and common structures / flow) so I'll change the F# outer code to this:
let finalResult =
Seq.initInfinite (fun i -> i)
|> Seq.scan
CalculateNextState
{ Weights = [r.NextDouble(); r.NextDouble()]; Bias = float 0; GlobalError = Double.MaxValue }
|> Seq.find (fun state -> state.GlobalError = float 0)
.. and then define this nested function:
let CalculateNextState (state: CalculationState) (iteration: int) =
// Do work here..
(Again, I've started by including explicit type annotations for the arguments but I'll be able to remove them later).
The C# code used the "Aggregate" function which corresponds to "List.fold" in F# and "Console.WriteLine" which corresponds to "printfn". With everything that we've covered already, it shouldn't be a big leap to see that the complete implementation of the "CalculateNextState" function will be as follows:
let CalculateNextState (state: CalculationState) (iteration: int) =
let resultForIteration =
List.fold
(fun stateSoFar input ->
let output = if (Output stateSoFar.Weights stateSoFar.Bias input.Values) then 1 else -1
let localError = float ((if input.Result then 1 else -1) - output)
{
Weights =
if (localError = float 0)
then stateSoFar.Weights
else UpdateWeights stateSoFar.Weights localError input.Values
Bias =
if (localError = float 0)
then stateSoFar.Bias
else stateSoFar.Bias + (learningRate * localError)
GlobalError = stateSoFar.GlobalError + Math.Abs(localError)
}
)
{ Weights = state.Weights; Bias = state.Bias; GlobalError = float 0 }
trainingData
printfn "Iteration %i\tError %i" iteration (int resultForIteration.GlobalError)
resultForIteration
It's still taking me a little while to get used to there being no "return" keyword and so I sometimes have to remind myself that the anonymous function passed to "List.fold" returns the { Weights, Bias, GlobalError } value and that the "CalculateNextState" function returns the "resultForIteration" that is on its last line.
Now that the function is fully defined, the type annotations can be removed from the "state" and "iteration" arguments. The "state" type is inferred because "List.fold" takes an initial value that has the properties Weights (float list) / Bias (float) / GlobalError (float) and the anonymous function also returns a value of that type and the only record type that matches those properties is "CalculationState". The "iteration" argument is inferred because it is used as an argument in the "printfn" call to populate a "%i" placeholder and "%i" placeholder values have to be integers.
Writing to console using printfn and "string interpolation"
You might have noticed that in the code above, the C# write-info-to-console line:
Console.WriteLine("Iteration {0}\tError {1}", iteration, resultForIteration.GlobalError);
was translated into this in F#:
printfn "Iteration %i\tError %i" iteration (int resultForIteration.GlobalError)
In principle, it's very similar; there are placeholders in the format string (which is what the "%i" values are in the F# code above) that will be populated with arguments passed to Console.WriteLine / printfn but there are a couple of key differences. The first is that the "%i% placeholder requires that the value used to populate it is an integer (alternatives are "%s" for strings, "%f" for floats and "%b" for booleans) but the second is much more exciting - the format string and the provided arguments are verified at compile time in the F# code whereas the C# code is only verified at run time. To make it really crystal clear what I mean by this, the following C# code will compile but fail when it's run -
// This will fail at runtime with "System.FormatException: 'Index (zero based) must be greater
// than or equal to zero and less than the size of the argument list.'" because there are two
// placeholders in the format string but only one value provided
Console.WriteLine("Hello {0}, {1}", "test");
On the other hand, the following F# won't even compile -
// Will refuse to compile: "This expression is a function value, i.e. is missing arguments."
printfn "Hello %s, %s" "test"
This makes me happy because I'm all about making the compiler catch simple mistakes instead of allowing them to surface at runtime.
Now, I will admit that I was using a somewhat old school method of writing messages there in C#. C#6 introduced its own interpretation of "string interpolation" that allows us to combine the "template string" with the placeholder values so that we don't accidentally include too many or too few placeholder value arguments. Instead of writing this:
// Old style
Console.WriteLine("Iteration {0}\tError {1}", iteration, resultForIteration.GlobalError);
.. we could write this:
// C# 6 string interpolation
Console.WriteLine($"Iteration {iteration}\tError {resultForIteration.GlobalError});
I would argue that this is even better again than the F# approach and it's unfortunate that F# doesn't currently have anything quite like this. That is one of the downsides to F# pioneering and pushing a lot of useful techniques that were later incorporated in to C#, I suppose!
(There is a proposal to add something similar to F# but it doesn't exist yet and I don't think that there is any suggestions that it will become available any time soon - see F# RFC FS-1001 - String Interpolation)
Sidebar: Selecting F# BCL functions
A little earlier, I nonchalantly said that
The C# code used the "Aggregate" function which corresponds to "List.fold" in F#
.. and you may (quite reasonably) have wondered how you or I were supposed to know that "Aggregate" in C# is equivalent to "fold" in F#.
You may also have picked up on the fact that sometimes I'm using "Seq" functions (such as "Seq.initInfinite") and sometimes I'm using "List" functions (such as "List.fold") and be wondering how I'm deciding which to use.
I'll address the second point first. As I do so, it's worth bearing in mind that I'm going to explain how I have been deciding up to this point and hopefully it's a sensible approach but there's always a chance that someone who knows better (maybe me in six months!) will have a slightly different take on things..
In a nutshell, I'm going to use "List" if I'm certain that I want to fully evaluate the set of items. In the "CalculateNextState" function, I want to take all of the weights in the current state and generate a completely updated set of weights to use in the next iteration - in that next iteration, I will be using all of the just-calculated weights to generate another completely updated set of weights. Every time, I will be considering every weight value and there would be no benefit to lazily evaluating the data and I think that lazy evaluation is one of the main benefits to using "Seq". When I don't know how many iterations will be required, I start by lazily evaluating an infinite set of items by calling "Seq.initInfinite" and then terminating enumeration when I get a state with a sufficiently low GlobalError. This approach only works because the sequence is evaluated "lazily" - it would make no sense for there to be a "List.initInfinite" because that list's contents would have to be fully populated at runtime and you'd run out of memory!
I suspect that a case could be made for always using "Seq" unless you find a compelling reason not to.. where a compelling case is that you need pattern matching* or if you're sure that using "Seq" is resulting in expensive operations being repeated because you are enumerating over a sequence multiple times and the operations in each enumeration are complex / expensive (if you used "List" then you would be sure that the work to build the list would only be done once, no matter how many times you enumerated over it).
* (which we haven't encountered yet but which is fairly common in F# code and which only works with instances of list and not of seq)
F# also supports arrays but these tend to used in fairly niche situations - such as when interoperating with other .NET code that requires an array or when you've found a performance bottleneck in your code relating to indexed access into your set of items (for both a seq and a list it's relatively slow to jump straight to the nth item because you have to start at the beginning and walk that many items into the list, whereas with an array you can jump straight there).. but arrays have their disadvantages, such as being mutable (bleurgh, filthy!) and having no cheap way to create a new version with a single new item (which also applies to seq but which is something that list can do well).
So (for now?) I'll be using a list if I have a known set of items and will be performing an operation on every item each iteration and a seq otherwise.. unless I encounter a really exciting reason to do otherwise*.
* (Spoiler alert: in a future post in the series, I will find a case where there is a huge difference in memory usage between list and array when loading data from disk - brace yourself for that thrill!)
To return to my first point in relation to "Selecting F# BCL functions" - how did I know that "List.fold" is equivalent to "Aggregate"? The simple answer is by looking through the docs.. the MSDN pages are pretty good (here is the one for List.fold) and the number of base library functions is not that large. You can often guess what many of them do (such as "List.average" and "List.distinct") but you might need to read the documentation for others (either on MSDN or just via the intellisense tooltips) for others. If you are familiar with LINQ then it shouldn't take you too long to learn the names of the F# equivalents of many of your old favourites!
Demonstrating the network's abilities
Before I went on a couple of tangents about writing to the console and learning the F# BCL, we had actually finished translating the code that trained the network (it may be an extremely simple one but it is still technically a network!). Now the only C# that remains to be translated is the code that passes pairs of inputs through the network to see what output it generates for each pair - just to ensure that it matches our expectations. This is how we left it last time:
const double startAt = 0;
const double endAt = 1;
const double increment = 0.25;
var range = Enumerable.Range(0, (int)((endAt - startAt) / increment) + 1).Select(value => value * increment);
var xyPairs = range.SelectMany(value => range, (x, y) => new[] { x, y });
Console.WriteLine(string.Join(
Environment.NewLine,
xyPairs.Select(inputs => $"{string.Join("\t", inputs)}\t{(Output(finalResult.Weights, finalResult.Bias, inputs) ? "Yes" : "No")}")
));
The first thing that will be nice about translating this into F# is that it has better support for defining ranges. In C#, we used "Enumerable.Range" but that only works with integers and so we then had to do some division. In F#, we're able to say "define a range by starting at x and incrementing by y until you get to z". So we could replace this:
const double startAt = 0;
const double endAt = 1;
const double increment = 0.25;
var range = Enumerable.Range(0, (int)((endAt - startAt) / increment) + 1).Select(value => value * increment);
.. with this:
let range = { float 0 .. float 0.25 .. float 1 }
We could then translate the rest of the C# shown above in a like-for-like fashion into F# or we could get a tiny bit fancier with some code that I found on Stack Overflow that takes one set of values and transforms it by combining every value with other value (so if your input set was the numbers 1 and 2 then the output would be {1,1} and {1,2} and {2,1} and {2,2}). This is sometimes referred to as taking the "cross product" and is the same concept as doing a "cross join" in SQL.
The code to do it is as follows:
// Inspired by https://stackoverflow.com/a/482922/3813189
let crossproductWithSelf xs = seq { for x1 in xs do for x2 in xs do yield x1, x2 }
Using this means that our "Display network generalisation" summary code looks like this:
let crossproductWithSelf xs = seq { for x1 in xs do for x2 in xs do yield x1, x2 }
let calculatedResults =
{ float 0 .. float 0.25 .. float 1 }
|> crossproductWithSelf
|> Seq.map (fun (x, y) ->
x.ToString() + ",\t" +
y.ToString() + ",\t" +
(if (Output finalResult.Weights finalResult.Bias [x; y]) then "Yes" else "No")
)
printfn ""
printfn "X,\tY,\tOutput"
printfn "%s" (String.concat Environment.NewLine calculatedResults)
Pretty neat and tidy, I think!
Done! What's next?
Phew! Well that felt like quite a lot of work. Getting to grips with a new language can be mentally taxing, particularly when it involves a new paradigm (like making the leap from OOP to functional programming) and I think that that's why it's taken me several attempts at getting started with F# to even get this far.
And although this is a good start, the "machine learning" aspect of the Single Layer Perceptron is very basic and it should be fun to try to dig a little deeper and attempt something more complicated. To that end, I have a few more posts that I'd like to write that will explain how to train a neural network (that has more layers than just the input and output layers) using the Backpropagation Algorithm and then use this to recognise handwritten digits from the famous MNIST image database.
As with the code here, I will be starting with C# from the Robosoup blog and translating it into a functional style before rewriting it as F#. I think that it's exciting stuff!
One more thing - in case you're curious to see the complete F# code that was scattered through this post, here it is:
open System
type private Input = { Values: list<float>; Result: bool }
type private CalculationState = {
Weights: List<float>
Bias: float
GlobalError: float
}
let Go (r: Random) =
let trainingData = [
{ Values = [0.08; 0.94]; Result = true }; { Values = [0.13; 0.95]; Result = true };
{ Values = [0.28; 0.66]; Result = true }; { Values = [0.3; 0.59]; Result = true };
{ Values = [0.31; 0.51]; Result = true }; { Values = [0.34; 0.67]; Result = true };
{ Values = [0.34; 0.63]; Result = true }; { Values = [0.36; 0.55]; Result = true };
{ Values = [0.38; 0.67]; Result = true }; { Values = [0.4; 0.59]; Result = true };
{ Values = [0.4; 0.68]; Result = true }; { Values = [0.41; 0.5]; Result = true };
{ Values = [0.42; 0.53]; Result = true }; { Values = [0.43; 0.65]; Result = true };
{ Values = [0.44; 0.56]; Result = true }; { Values = [0.47; 0.61]; Result = true };
{ Values = [0.47; 0.5]; Result = true }; { Values = [0.48; 0.66]; Result = true };
{ Values = [0.52; 0.53]; Result = true }; { Values = [0.53; 0.58]; Result = true };
{ Values = [0.55; 0.6]; Result = true }; { Values = [0.56; 0.44]; Result = true };
{ Values = [0.58; 0.63]; Result = true }; { Values = [0.62; 0.57]; Result = true };
{ Values = [0.68; 0.42]; Result = true }; { Values = [0.69; 0.21]; Result = true }
{ Values = [0.7; 0.31]; Result = true }; { Values = [0.73; 0.48]; Result = true };
{ Values = [0.74; 0.47]; Result = true }; { Values = [0.74; 0.42]; Result = true };
{ Values = [0.76; 0.34]; Result = true }; { Values = [0.78; 0.5]; Result = true };
{ Values = [0.78; 0.26]; Result = true }; { Values = [0.81; 0.48]; Result = true };
{ Values = [0.83; 0.32]; Result = true }; { Values = [0.83; 0.28]; Result = true };
{ Values = [0.85; 0.07]; Result = true }; { Values = [0.85; 0.45]; Result = true };
{ Values = [0.88; 0.4]; Result = true }; { Values = [0.89; 0.92]; Result = true };
{ Values = [0.9; 0.33]; Result = true }; { Values = [0.91; 0.05]; Result = true };
{ Values = [0.92; 0.44]; Result = true }; { Values = [0.95; 0.94]; Result = true };
{ Values = [0.96; 0.08]; Result = true };
{ Values = [0.02; 0.76]; Result = false }; { Values = [0.06; 0.22]; Result = false };
{ Values = [0.07; 0.16]; Result = false }; { Values = [0.09; 0.43]; Result = false };
{ Values = [0.1; 0.08]; Result = false }; { Values = [0.14; 0.07]; Result = false };
{ Values = [0.15; 0.23]; Result = false }; { Values = [0.17; 0.18]; Result = false };
{ Values = [0.17; 0.11]; Result = false }; { Values = [0.21; 0.28]; Result = false };
{ Values = [0.22; 0.17]; Result = false }; { Values = [0.25; 0.09]; Result = false };
{ Values = [0.28; 0.28]; Result = false }; { Values = [0.28; 0.27]; Result = false };
{ Values = [0.29; 0.22]; Result = false }; { Values = [0.29; 0.29]; Result = false };
{ Values = [0.3; 0.29]; Result = false }; { Values = [0.31; 0.14]; Result = false };
{ Values = [0.33; 0.19]; Result = false }; { Values = [0.33; 0.06]; Result = false };
{ Values = [0.39; 0.15]; Result = false }; { Values = [0.52; 0.1]; Result = false };
{ Values = [0.65; 0.07]; Result = false }; { Values = [0.71; 0.1]; Result = false };
{ Values = [0.74; 0.05]; Result = false }
]
let inputLengths =
trainingData
|> List.map (fun input -> input.Values.Length)
|> List.distinct
|> List.length
if (inputLengths > 1) then raise (Exception "Inconsistent pattern input lengths!")
let learningRate = 0.1
let Output weights bias inputs =
let sum = (List.zip weights inputs |> List.map (fun (weight, input) -> weight * input) |> List.sum) + bias
sum >= float 0
let UpdateWeights weights localError inputs =
if (localError = float 0)
then weights
else
List.zip weights inputs
|> List.map (fun (weight, input) -> weight + (learningRate * localError * input))
let CalculateNextState state iteration =
let resultForIteration =
List.fold
(fun stateSoFar input ->
let output = if (Output stateSoFar.Weights stateSoFar.Bias input.Values) then 1 else -1
let localError = float ((if input.Result then 1 else -1) - output)
{
Weights =
if (localError = float 0)
then stateSoFar.Weights
else UpdateWeights stateSoFar.Weights localError input.Values
Bias =
if (localError = float 0)
then stateSoFar.Bias
else stateSoFar.Bias + (learningRate * localError)
GlobalError = stateSoFar.GlobalError + Math.Abs(localError)
}
)
{ Weights = state.Weights; Bias = state.Bias; GlobalError = float 0 }
trainingData
printfn "Iteration %i\tError %i" iteration (int resultForIteration.GlobalError)
resultForIteration
let finalResult =
Seq.initInfinite (fun i -> i)
|> Seq.scan
CalculateNextState
{ Weights = [r.NextDouble(); r.NextDouble()]; Bias = float 0; GlobalError = Double.MaxValue }
|> Seq.find (fun state -> state.GlobalError = float 0)
let crossproductWithSelf xs = seq { for x1 in xs do for x2 in xs do yield x1, x2 }
let calculatedResults =
{ float 0 .. float 0.25 .. float 1 }
|> crossproductWithSelf
|> Seq.map (fun (x, y) ->
x.ToString() + ",\t" +
y.ToString() + ",\t" +
(if (Output finalResult.Weights finalResult.Bias [x; y]) then "Yes" else "No")
)
printfn ""
printfn "X,\tY,\tOutput"
printfn "%s" (String.concat Environment.NewLine calculatedResults)
Go (new Random(0))
Posted at 23:24
Learning F# via some Machine Learning: The Single Layer Perceptron
TL;DR
I know C# well and I want to learn F#. I want to wrap my head about some of the underlying algorithms that enable the machine learning that seems so prevalent in the world today (voice recognition, computer vision, sales prediction, semantic analysis, translation). I'm going to try to do both together and prove to myself that I have a good understanding of them both by writing about it.
The lure of F#
For a few years now, I've been wanting to have a proper crack at learning F#. There's a lot about it that sounds very appealing - immutability-by-default and better representation / handling of null values while still being able to use Visual Studio and use the .NET framework library (as well as other .NET assemblies). I've tried a couple of times in the past but without any concrete project to work on, I find that I struggle to motivate myself without a target to work towards that is more tangible than "feel like I've learned a bit of a new language".
To address this, I've decided to combine learning-some-F# with learning-some-machine-learning-basics so that I have a more solid goal. As I go, I thought that I'd write a few posts about the process for two reasons; firstly, being able to explain something clearly is a good indicator that you understand it yourself and, secondly, there is a chance (admittedly slim!) that this might be useful to someone else in a similar position to me, who is familiar with C# and wants to get to grips with F# - I wouldn't even consider myself intermediately competent yet and so I'm still encountering the pain points of being an F# beginner and seeing how I deal with them might be helpful to others.
Last year, I wrote Face or no face (finding faces in photos using C# and Accord.NET), which classified image regions using a linear support vector machine. This was technically a machine learning solution but it's only one particular algorithm and there are limitations to the sorts of problem that it can tackle. I want to work up to implementing a Back-Propagation Neural Network that will categorise hand written digits (0-9) but I'm going to start a little simpler.
While trying to decide how I was going to get started, I read (or scan-read, in many cases, if I'm being honest) what felt like hundreds of articles about neural networks. One of the issues with trying to learn something like this through the research of others is that the people writing about it already have a level of knowledge far above my own on the matter and it feels like there is a lot of knowledge that it assumed that the reader will have. Another issue is that there is often maths involved that can seem sufficiently complicated that it is off-putting. In my posts, I'm going to try to keep things as simple as possible (which may well mean brushing some "whys" under the carpet - leaving it as an exercise to the reader to find out more from other people, once the basics are understood). One series of posts that I did find very approachable, though, was on a site "Robosoup" - which is for a consultancy based in London that specialise in machine learning. The first post in the series is "The Single Layer Perceptron C#" and I'm actually going to start with some of the code there and the example data. I'm going to try to explain things my own way but much of the content here will owe a debt to that Robosoup article (I got in touch with John Wakefield at Robosoup and he said that he was happy for me share his code - rest assured that I'm not just stealing it without asking for permission first!).
The Single Layer Perceptron
The concept of an "artificial neural network" is, essentially, that there is a system of neurons that are connected together and that have a series of inputs that send signals into the system and which eventually get (somehow) transformed into a series of outputs. Each output represents a particular result. If, for example, the neural network was intended to categorise images then the inputs will all be derived from the image data in some way and there may be an output for "dog" and an output for "cat" and these output will end up with a stronger or weaker signal depending upon the input data. The connections between the neurons will have different "weights" and so different input values will somehow result in different outputs. These different weights will have to calculated as part of the network's "training". This sort of description is often accompanied by complicated-looking diagrams such as this:
(Taken from Cesar Harada's Flickr under license conditions)
This raises a lot of questions and feels like far too complicated a place to start! (Though, in later posts, I will be talking about multi-layered multi-output neural networks similar to what is shown above).
The "Single Layer Perceptron" is simpler - it only has one input "layer" and one output "layer", where a layer is a list of "neurons". A neuron is something that takes an input value (a value from -1 to 1), multiplies it by a "weight" (also a value from -1 to 1) and then passes that value onto every node that it is connected to in the layer ahead of it. Pretty much the simplest possible network imaginable that would fit this description would be just two neurons in the input layer and a single neuron in the output layer. Like this:
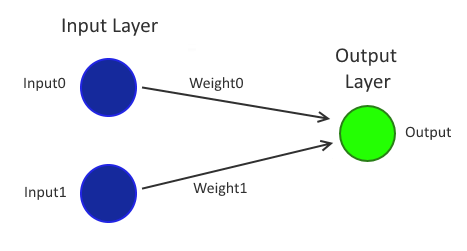
Now this might almost seem too simple! Can this really do anything useful? Well, actually, it's entirely possible to configure a network like this to act as a classifier for any data that is "linearly separable" in as many dimensions as there are inputs. This is already sounding like mumbo jumbo, so I'll go over those terms..
A "classifier" will look at its inputs and give a yes/no answer (for example, an "is this a cat?" classifier might look at a photograph and report whether there appears to be a cat in it or not).
"Linearly separable" is simplest to understand in 2D - if the data is plotted on a graph then it's "linearly separable" if it's possible to draw a straight line across the graph that puts all of the values for "yes" lie on one side and all inputs for "no" lie on the other side. When I wrote about linear support vector machines, I talked about a fictional decision history for a manager, where they would give the go-ahead (or not) to a new feature based upon how much of it could be billed to Clients and what strategic value it had to the company.

This data is linearly separable because it's possible to draw a line on the graph where all of the data above gets a "yes" response and all of the data below gets a "no".
Some data sets will not fit this model and so are not linearly separable. That won't make it impossible to classify using a neural network but it will make it impossible for a perceptron to classify (without some form of processing of the data before classification - which is out of the scope of what I want to cover today).
2D data like this would involve a perceptron with two inputs. 3D data that is linearly separable would have all of its data points separable by a plane in the 3D space - all points on one side would be "yes" and all points on the other would be "no"; this data would involve a perceptron with three inputs.
While it's not as easy to envisage this in more dimensions, the same principle holds. For this sort of multi-dimensional data, the additional dimensions tend to be additional measurable factors that are thought to have affected the outcome (for example, maybe the manager in the example above is predictably less likely to give the go-ahead to features on Monday and Tuesday because they're always snowed under with emails for those first two days of the week and they're less likely to sign off on things when they're hungry; that would mean that there would be four dimensions to consider, which would be "amount of cost that can be put onto Clients", "strategic value of the work", "day of the week" and "time since last ate" - these four dimensions would require a perceptron with four inputs to model the data).
Training a perceptron
I said above that it's possible to configure a network to act as a classifier for linearly separable data. All that is required to configure the network is to assign the weight0 and weight1 values (at least, that is the case for 2D data - since each input has its own weight value then 2D data requires two inputs but if the input is three dimensional then there will be three weight values that must be set and if there were four dimensions then there would be four weight values, etc..). When it is correctly configured, it will be possible to apply any values to the input neurons and to get a single output value. If this output value is higher than a particular threshold then the output will be considered a positive response and otherwise it will be considered a negative response.
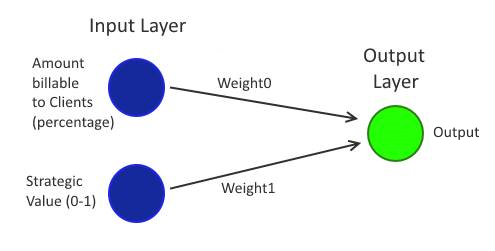
Returning to the Manager Decision data, one of the inputs will be for the "amount of cost that can be put onto Clients" while the other will be the "strategic value of the work". For the data and the code that I'm going to look at further down, all inputs and outputs are in the 0-1 range (this is convenient enough for "amount of cost that can be put onto Clients" but it may be more difficult in the real world to fit all features into a 0-1 range for "strategic value of the work" - but since that data is just a fictional example, we don't need to worry about that too much).
The question, then, is how should we determine the weights for each neuron? This is where the "machine learning" part comes into it. What we're going to do is "train" a network by using historical data.
At its essence, the way that a trained network like this is produced is by -
- Setting all of the weights to be random values between 0 and 1
- Passing all of the historical data (aka "training data") through it and, for each "pattern" (which is the name given to a series of inputs)
- Calculating the "local error" (the error for that particular pattern)
- Adjusting the weights based upon this local error
- Taking the "total error" or "global error" (the sum of all of the local errors from the training data) and either finding that it is less than a predetermined threshold (in which case the network training is considered complete - hurrah!) or going back to step 2
There are a lot of things to consider there - what precisely are the "local errors", how are the weights adjusted each iteration and what threshold should we stop at? Let's work through each of those in order..
The local error for a particular pattern is how far away the output of the network is from the expected result. Since all of the input data has a yes/no expected output, we'll translate "yes" into 1 and "no" into 0. For each pattern, we take its inputs and set the input neurons with those values. Then we calculate the output for the network (by multiplying the first input by the first weight and the second input by the second weight and then adding those two values together). Then we compare this output value to the expected 1 or 0 - so, if we get 0.3 as the output value for the first pattern and we expected 1 then that's an error of 0.7 (since 0.3 is 0.7 away from the expected value of 1). If we get 0.6 for the output value for the second pattern and we expected 0 then that's an error of 0.6 (since 0.6 is 0.6 away from the expected value of 0).
In order to adjust the weights after each pattern has been run through the network, a fairly simple equation is used - each new weight is calculated using:
weight[i] = weight[i] + (learningRate * localError * patternInput[i])
For this network, there are only two inputs and so there will only be two values for "i".
The "learning rate" is a value between 0 and 1 that determines how quickly the weights change as the network is trained. Clearly, a value of 0 would mean that the weights don't change each iteration, which would be useless. The larger the value of the learning rate, the more that the weights will be adjusted each iteration - however, larger is not always better because the adjustments may swing too far each time and, instead of slowing homing in on a well-trained network, the weights may alternate back and forth and never significantly improve. In the example code that I'm going to look at, I'm using a learning rate of 0.1* but this is a value that you may wish to try playing with when experimenting with training - there seem to be many guidelines when it comes to machine learning and many sensible approaches to classes or problem but there aren't always hard and fast rules for all of the variables and there are often things to tweak here and there that may affect how quickly you get a result (or if you get one at all).
* (To be honest, I've "decided" to use a learning rate of 0.1 because much of the initial C# code below comes from the Robosoup article that I mentioned earlier and a 0.1 learning rate is used there!)
The acceptable "global error" is another "tunable parameter" in that a higher acceptable threshold should mean that training will complete more quickly but also that the resulting network will be less accurate. On the other hand, it may be impossible to train a network (particularly so simple a network as a single perceptron) to match all of the training data perfectly and so a reasonable threshold must be accepted. In the example code below, a network that perfectly matches the training data is possible and won't take long to train and so we'll aim for a zero global error.
I'm not going to go into any more detail about how you may set these tunable parameters (learning rate and global error threshold) because there's a lot of material to cover and I want to try to stick to practical concepts and code (and because I'm still not very confident that I've got a great system for deciding them!).
Input bias
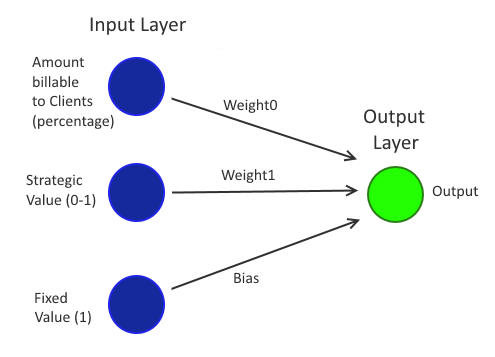
Using the training method described above, you will always get a line that cuts through the data at the point (0, 0). This would not work for the "Manager Decision History" graph because there is no way that a line starting at the bottom left of the graph could correctly cut through the data with all of the red points on one side and all of the green points on the other (on that graph all values are 0-1 and so the bottom left is the 0, 0 point).
A way to address this is to introduce an additional "bias" value. This is effectively like adding an additional neuron whose input value is always one and that has its own weight, just like every other input. Every time that a pattern is passed through the system while it is being trained, when the weights are adjusted, the bias should also be adjusted using the following formula:
bias = bias + (learningRate * localError)
(The formula is basically the same as the weight-adjusting formula except that the "patternInput[i]" value is removed because the bias neuron's input value is always 1)
This bias value means that the line that separates the yes/no values no longer has to go through (0, 0) but it has no other effect on training process, other than there being more slightly more work to do (although, without it, we wouldn't be able to get an answer for many sets of data - so it's not really more work at all!).
I've just said that it would not be possible to train a simple network of this form for some data sets without a bias.. which begs the question "for what data sets should a bias node be introduced?" - I think that it makes sense to always include one since, presumably, you don't know what solution the neural net should produce and so you don't know whether or not it would strictly be necessary to have a bias. So it's better to err on the safe side. If the data does not require a bias then the trained network should end up with a small (ie. close to zero) bias value and it will have little impact.
(This "input bias" is very different to moral biases that can creep into machine learning predictions due to biases, that are often unintentionally included, in the training data - see "Forget Killer Robots—Bias Is the Real AI Danger")
From C# to F#..
The format that I intend to follow for these posts is roughly as follows:
- Talk about the theory (we've already done that today!)
- Look at some fairly standard C# code
- Look at making the C# code more functional by removing variable mutations (including loops)
- Rewrite the "functional C#" in F#
As an F# beginner, this is the approach that I've been using for trying to learn it - until I've internalised it further, it still feels like a big ask to take regular C# and rewrite it into idiomatic F# and so the "functional C#" stage helps me a lot. The syntax of F# is not that big of a deal but thinking in (functional) F# is still something that I'm working towards.
(It's worth noting that, for me, getting my head around F# and functional programming is the priority. Much of the C# that we'll be looking will be doing in-place mutations - which, arguably, is a good model for doing the processing that we'll be looking at when it's done on a single thread - and since we'll be moving to using immutable structures then there is a good chance that the performance will be worse in the final F# code. If that turns out to be the case, though, then I'm not going to worry about it. I think that performance concerns are for when you have a better grasp of the technology that you're working with and I'm not there yet with F# - so I don't mind if I end up with worse-performing code in the context of this post so long as I've learned a lot from writing it!)
// Code slightly modified from that at
// http://www.robosoup.com/2008/09/the-single-layer-perceptron-c.html
public static class Perceptron
{
public static void Go(Random r)
{
// Load sample input patterns and expected outputs
var trainingData = new[]
{
Pattern(0.08, 0.94, true), Pattern(0.13, 0.95, true), Pattern(0.28, 0.66, true),
Pattern(0.3, 0.59, true), Pattern(0.31, 0.51, true), Pattern(0.34, 0.67, true),
Pattern(0.34, 0.63, true), Pattern(0.36, 0.55, true), Pattern(0.38, 0.67, true),
Pattern(0.4, 0.59, true), Pattern(0.4, 0.68, true), Pattern(0.41, 0.5, true),
Pattern(0.42, 0.53, true), Pattern(0.43, 0.65, true), Pattern(0.44, 0.56, true),
Pattern(0.47, 0.61, true), Pattern(0.47, 0.5, true), Pattern(0.48, 0.66, true),
Pattern(0.52, 0.53, true), Pattern(0.53, 0.58, true), Pattern(0.55, 0.6, true),
Pattern(0.56, 0.44, true), Pattern(0.58, 0.63, true), Pattern(0.62, 0.57, true),
Pattern(0.68, 0.42, true), Pattern(0.69, 0.21, true), Pattern(0.7, 0.31, true),
Pattern(0.73, 0.48, true), Pattern(0.74, 0.47, true), Pattern(0.74, 0.42, true),
Pattern(0.76, 0.34, true), Pattern(0.78, 0.5, true), Pattern(0.78, 0.26, true),
Pattern(0.81, 0.48, true), Pattern(0.83, 0.32, true), Pattern(0.83, 0.28, true),
Pattern(0.85, 0.07, true), Pattern(0.85, 0.45, true), Pattern(0.88, 0.4, true),
Pattern(0.89, 0.92, true), Pattern(0.9, 0.33, true), Pattern(0.91, 0.05, true),
Pattern(0.92, 0.44, true), Pattern(0.95, 0.94, true), Pattern(0.96, 0.08, true),
Pattern(0.02, 0.76, false), Pattern(0.06, 0.22, false), Pattern(0.07, 0.16, false),
Pattern(0.09, 0.43, false), Pattern(0.1, 0.08, false), Pattern(0.14, 0.07, false),
Pattern(0.15, 0.23, false), Pattern(0.17, 0.18, false), Pattern(0.17, 0.11, false),
Pattern(0.21, 0.28, false), Pattern(0.22, 0.17, false), Pattern(0.25, 0.09, false),
Pattern(0.28, 0.28, false), Pattern(0.28, 0.27, false), Pattern(0.29, 0.22, false),
Pattern(0.29, 0.29, false), Pattern(0.3, 0.29, false), Pattern(0.31, 0.14, false),
Pattern(0.33, 0.19, false), Pattern(0.33, 0.06, false), Pattern(0.39, 0.15, false),
Pattern(0.52, 0.1, false), Pattern(0.65, 0.07, false), Pattern(0.71, 0.1, false),
Pattern(0.74, 0.05, false)
};
// Randomise weights
var weights = new[] { r.NextDouble(), r.NextDouble() };
var bias = 0d;
// Set learning rate
var learningRate = 0.1;
var iteration = 0;
double globalError;
do
{
globalError = 0;
for (var p = 0; p < trainingData.Length; p++)
{
// Calculate output
var inputs = trainingData[p].Item1;
var output = Output(weights, bias, inputs[0], inputs[1]) ? 1 : -1;
// Calculate error
var expected = trainingData[p].Item2;
var localError = (expected ? 1 : -1) - output;
if (localError != 0)
{
// Update weights
for (var i = 0; i < 2; i++)
{
weights[i] += learningRate * localError * inputs[i];
}
bias += learningRate * localError;
}
// Convert error to absolute value
globalError += Math.Abs(localError);
}
Console.WriteLine("Iteration {0}\tError {1}", iteration, globalError);
iteration++;
} while (globalError != 0);
Console.WriteLine();
Console.WriteLine(
$"Final weights: {weights[0]}, {weights[1]}, Bias: {bias} => Error: {globalError}"
);
// Display network generalisation (note: the "Manager Decision" data has input values that
// are all in the range 0-1 in both dimensions and so we will only look at values in this
// range in this preview here)
Console.WriteLine();
Console.WriteLine("X,\tY,\tOutput");
for (double x = 0; x <= 1; x += .25)
{
for (double y = 0; y <= 1; y += .25)
{
var output = Output(weights, bias, x, y);
Console.WriteLine("{0},\t{1},\t{2}", x, y, output ? "Yes" : "No");
}
}
Console.WriteLine();
}
private static bool Output(double[] weights, double bias, double x, double y)
{
var sum = (x * weights[0]) + (y * weights[1]) + bias;
return (sum >= 0);
}
/// <summary>Helper for initialising training data</summary>
private static Tuple<double[], bool> Pattern(double x, double y, bool output)
{
return Tuple.Create(new[] { x, y }, output);
}
}
This code is fairly straightforward and it goes through the steps that I described before:
- Set weights to be random values and the bias to be zero
- Take each training data entry's input and calculate the output using the current weights (and bias), adjusting the weights (and bias) if the calculated output did not match the expected output
- Compare the total error against a threshold (of zero) and go back to step 2 if it's too high
The way that I'm going to change this code from "regular" (I would call it "object oriented" C# but the code shown here is probably closer to being "procedural") to "functional*" C# is by looking for things that would seem out of place in functional code and replacing them.
* ("functional" is often interpreted as meaning that you avoid side effects and avoid mutation - we can argue about that definition another day if you like but it's a good enough place to start for now!)
Immediately, the following things jump out at me:
- Variables whose values are explicitly changed during processing (eg. "iteration" and "globalError")
- Variables whose values change as part of looping constructs (eg. "i", "x" and "y")
- The do..while loop will not be useful if values are not to be mutated with it and so that will need to be replaced with something else
I suppose the question, then, is how can we possibly write code like this without changing / mutating / updating values?
The first thing to recognise is that LINQ made a more functional style of processing much more mainstream within C# and seem less alien. Before LINQ, if you had an array of values and you wanted an array containing the squares of these values (contrived example, I know, but bear with me) then you may well have achieved this in a fairly procedural manner - eg.
var values = new[] { 1, 2, 3 };
var squaredValues = new int[values.Length];
for (var i = 0; i < values.Length; i++)
squaredValues[i] = values[i] * values[i];
Each time the loop is executed, the value of "i" changes and the "squareValues" array is updated.
Until the for loop has been fully executed, the "squaredValues" array is only partially initialised.
Within the loop, it's technically possible to change the value of "i" and move it backwards or forwards (such as by throwing in a bonus "i++" to keep future code maintainers on their toes) and this can be the cause of potential coding errors in loops more complicated than the one shown here.
Since all we want to do is transform every single value in one array and create a new array from the results, it would be nice if we could be more descriptive in what we are trying to do and to remove some "book keeping" (such as tracking the "i" value using the for loop). This is what would happen if LINQ was used to perform the same work -
var values = new[] { 1, 2, 3 };
var squaredValues = values
.Select(value => value * value)
.ToArray();
Note that there is no mutation occurring here. Each time that the lambda that is passed to the "Select" method is called, a new "value" reference is created (unlike "i", which was a single variable shared across each iteration of the loop).
This is one technique that will be useful to remove mutation from code.
Another is the "Aggregate" method for enumerating a list of items and reducing it to a single reference. To try to illustrate; if I had a collection of words and I wanted to get the total number of words and the total number of letters then I might write procedural code like this:
static void ShowLetterAndWordCount(IEnumerable<string> words)
{
var numberOfLetters = 0;
var numberOfWords = 0;
foreach (var word in words)
{
numberOfLetters += word.Length;
numberOfWords++;
}
Console.WriteLine("Total number of letters: " + numberOfLetters);
Console.WriteLine("Total number of words: " + numberOfWords);
}
.. or I could achieve the same thing without any mutating variables by using the following code:
static void ShowLetterAndWordCount(IEnumerable<string> words)
{
var summary = words.Aggregate(
seed: new { NumberOfLetters = 0, NumberOfWords = 0 },
func: (valueSoFar, nextWord) => new
{
NumberOfLetters = valueSoFar.NumberOfLetters + nextWord.Length,
NumberOfWords = valueSoFar.NumberOfWords + 1
}
);
Console.WriteLine("Total number of letters: " + summary.NumberOfLetters);
Console.WriteLine("Total number of words: " + summary.NumberOfWords);
}
What "Aggregate" does is it takes a "seed" value and the first value of the list of items and combines them using the "func" lambda. It then takes this result and combines it with the second value of the list, also using the "func" lambda. It will then take this result and combines it with the third value of the list, etc.. until one final combined value is returned. In the code above, I've used an anonymous type for the seed (and so the final "summary" reference will also be an instance of that anonymous type and so have "NumberOfLetters" and "NumberOfWords" properties) but the seed can be a class or a primitive or any type that you need.
All of the "book keeping" required by the Aggregate method is handled by the method itself - there is no loop variable to worry about and there are no variables outside of the loop (such as "numberOfLetters" and "numberOfWords") that must be tracked. You need only to tell it what the initial "seed" value should be and how it should combine the "value so far" with a single item from the input list.
This is the advantage that it has over the procedural version (which may initially appear "less complicated") - you only need to consider what actually happens within a single operation and you don't have to look after any variables that must be maintained across the entire loop (which was the case with "numberOfLetters" and "numberOfWords" in the first version).
At its core, this means that the scope of variables is reduced and when they don't change (ie. they are immutable) there are less moving parts for you to mentally consider when trying to reason about any particular line of code.
I'm finding that the F# version of Aggregate (called "fold") is a very powerful and useful technique and so having a good grasp on how it works is very useful. Just to make it extra clear (apologies if this is belabouring the point but Aggregate doesn't, in my experience, tend to be commonly used in C# and so it may not be familiar to some), here's another example:
var values = new[] { 1, 2, 3, 4, 5 };
var sumOfValues = words.Aggregate(
seed: 0,
func: (valueSoFar, value) => valueSoFar + value
);
This will return 15 because it will just add all of the values together. It begins with a seed value of 0 and adds it to the first value (which is 1) to get 1. It then adds this "value so far" to the second value (which is 2) to get 3. It adds this to the third value (which is 3) to get 6 and adds this to the fourth value (which is 4) to get 10 and adds this to the fifth value (which is 5) to get 15.
Not a particularly useful piece of code - and one that could have been written more clearly as:
var values = new[] { 1, 2, 3, 4, 5 };
var sumOfValues = words.Sum();
.. but hopefully it reinforces how the Aggregate method operates on data. And hopefully it makes it clear how powerful Aggregate can be because so many other operations may be built on top of it, such as Min or Max -
static int? Min(IEnumerable<int> values)
{
return values.Aggregate(
seed: (int?)null,
func: (valueSoFar, nextValue) => (valueSoFar.HasValue && valueSoFar < nextValue)
? valueSoFar
: nextValue
);
}
static int? Max(IEnumerable<int> values)
{
return values.Aggregate(
seed: (int?)null,
func: (valueSoFar, nextValue) => (valueSoFar.HasValue && valueSoFar > nextValue)
? valueSoFar
: nextValue
);
}
To functional code.. one step at a time
Back to the Single Layer Perceptron code.. The way that I'm approaching this is to take one logical section of code and replace the procedural style of code with functional constructs.
The first that I'll tackle is the do..while loop and the mutation of the outer "iteration", "weights", "bias" and "globalError" variables.
This will be straightforward if we use the Aggregate method where the "value so far" contains a "Weights" array, a "Bias" value and a "GlobalError" value that will be re-calculated each iteration.
The input list passed to Aggregate will be an incrementing list of integers representing the current iteration number. The "func" lambda will take the previous Weights / Bias / GlobalError state and calculate the next Weight / Bias / GlobalError state. If the "previousState" already has a low enough GlobalError then the "func" lambda won't have to do any more calculating and can just return the previousState reference immediately (meaning that we don't have to do any more work and we can just let Aggregate finish as many iterations as it is configured to do so until the Aggregate call completes - if that sounds a bit unclear then hopefully it will make more sense after you see the code and I talk more about it below).
const double learningRate = 0.1;
const int maxNumberOfIterationsToPerform = 100; // See notes below code
var finalResult = Enumerable.Range(0, maxNumberOfIterationsToPerform)
.Aggregate(
seed: new
{
Weights = new[] { r.NextDouble(), r.NextDouble() },
Bias = 0d,
GlobalError = double.MaxValue
},
func: (previousState, iteration) =>
{
// The network is already trained - no more calculations required
if (previousState.GlobalError == 0)
return previousState;
var weights = previousState.Weights;
var bias = previousState.Bias;
var globalError = 0d;
for (var p = 0; p < trainingData.Length; p++)
{
// Calculate output
var inputs = trainingData[p].Item1;
var output = Output(weights, bias, inputs[0], inputs[1]) ? 1 : -1;
// Calculate error
var expected = trainingData[p].Item2;
var localError = (expected ? 1 : -1) - output;
if (localError != 0)
{
// Update weights (taking a copy of the weights array rather than altering its values)
weights = weights.ToArray();
for (var i = 0; i < 2; i++)
{
weights[i] += learningRate * localError * inputs[i];
}
bias += learningRate * localError;
}
// Convert error to absolute value
globalError += Math.Abs(localError);
}
Console.WriteLine("Iteration {0}\tError {1}", iteration, globalError);
return new { Weights = weights, Bias = bias, GlobalError = globalError };
}
);
(You may notice that I also changing "learningRate" from being a variable to be a const - since this will never change, it makes sense).
I've had to make a compromise in how I've written this code - I've had to specify a "maxNumberOfIterationsToPerform" value because the Aggregate method has no way to say "stop processing now, we have an answer that we're happy with". This is why there is the check at the top of the "func" lambda that says "if previousState's GlobalError is low enough then do no more calculation" - the Aggregate method will keep running through every single value in the input list. But how do we know that 100 iterations will be enough to get a zero Global Error? We don't!
What would be really helpful would be if we could have a variation of Aggregate that returns an IEnumerable of all of the intermediate calculation states (all of the "previousState" values) so that we could stop enumerating as soon as one of them has a GlobalError of zero - that way we wouldn't have to limit ourselves to a low maxNumberOfIterationsToPerform value. Something that would let us write code like this:
const double learningRate = 0.1;
var finalResult = Enumerable.Range(0, int.MaxValue)
.AggregateAndReturnIntermediateStates(
seed: new
{
// Same as in earlier code sample..
},
func: (previousState, iteration) =>
{
// Same as in earlier code sample but without the need to check GlobalError..
}
)
.First(state => state.GlobalError == 0);
I searched through the LINQ and the F# library documentation and I couldn't find anything in LINQ that I could use to do this but I did find something in F# called "scan". To implement it as a LINQ-esque C# extension method, though, is simple. If we start by considering what an implementation of Aggregate would look like:
public static TAccumulate Aggregate<TSource, TAccumulate>(
this IEnumerable<TSource> source,
TAccumulate seed,
Func<TAccumulate, TSource, TAccumulate> func)
{
var valueSoFar = seed;
foreach (var value in source)
valueSoFar = func(valueSoFar, value);
return valueSoFar;
}
.. we need only to change the return type from TAccumulate to IEnumerable<TAccumulate> and to throw in some "yield return" magic to produce "Scan":
public static IEnumerable<TAccumulate> Scan<TSource, TAccumulate>(
this IEnumerable<TSource> source,
TAccumulate seed,
Func<TAccumulate, TSource, TAccumulate> func)
{
yield return seed;
var valueSoFar = seed;
foreach (var value in source)
{
valueSoFar = func(valueSoFar, value);
yield return valueSoFar;
}
}
This means that I can now write:
const double learningRate = 0.1;
var finalResult = Enumerable.Range(0, int.MaxValue)
.Scan(
seed: new
{
// Same as in earlier code sample..
},
func: (previousState, iteration) =>
{
// Same as in earlier code sample (but still without the need to check GlobalError)..
}
)
.First(state => state.GlobalError == 0);
Hurrah! That's a good step forward!
Now I need to tackle the inner section:
var weights = previousState.Weights;
var bias = previousState.Bias;
var globalError = 0d;
for (var p = 0; p < trainingData.Length; p++)
{
// Calculate output
var inputs = trainingData[p].Item1;
var output = Output(weights, bias, inputs[0], inputs[1]) ? 1 : -1;
// Calculate error
var expected = trainingData[p].Item2;
var localError = (expected ? 1 : -1) - output;
if (localError != 0)
{
// Update weights (taking a copy of the weights array rather than altering its values)
weights = weights.ToArray();
for (var i = 0; i < 2; i++)
{
weights[i] += learningRate * localError * inputs[i];
}
bias += learningRate * localError;
}
// Convert error to absolute value
globalError += Math.Abs(localError);
}
Console.WriteLine("Iteration {0}\tError {1}", iteration, globalError);
return new { Weights = weights, Bias = bias, GlobalError = globalError };
I'm going to start from the inside and work outward this time. The first thing that I want to get rid of is the loop that is used to update weights. What this loop is effectively doing is walking through two arrays ("weights" and "inputs") and performing an operation on a single pair of items from each (each loop iteration, we do something with one weight value and one input value).
This is just what the "Zip" LINQ function does and so we can use that here. We'll replace:
// Update weights (taking a copy of the weights array rather than altering its values)
weights = weights.ToArray();
for (var i = 0; i < 2; i++)
{
weights[i] += learningRate * localError * inputs[i];
}
.. with this:
weights
.Zip(inputs, (weight, input) => weight + (learningRate * localError * input))
.ToArray();
To maker the "inner section" simpler, I'm going to hide that logic into a function:
private static double[] UpdateWeights(double[] weights, double learningRate, double localError, double[] inputs)
{
if (localError == 0)
return weights;
return weights
.Zip(inputs, (weight, input) => weight + (learningRate * localError * input))
.ToArray();
}
I've also pulled the "is localError zero" check into the method. It feels a little unnecessary when there are only two weights and two inputs but this new version of the weight-updating code may be called with any number of inputs and so it may make sense to avoid looping through them all when the localError is zero (because we won't be making any changes to the weights in that case).
The next thing to do is to get rid of the other for-loop and the values that it mutates on each iteration. This part:
var weights = previousState.Weights;
var bias = previousState.Bias;
var globalError = 0d;
for (var p = 0; p < trainingData.Length; p++)
{
// Apply current pattern and alter weights, bias and globalError accordingly..
}
If we group the "weights / bias / globalError" values into a single value then we can replace this with an Aggregate call, like we saw earlier:
var resultForIteration = trainingData.Aggregate(
seed: new { Weights = previousState.Weights, Bias = previousState.Bias, GlobalError = 0d },
func: (stateSoFar, pattern) =>
{
// Apply current pattern and calculate new weights, bias and globalError values..
// .. and return new object wrapping these values
return new { Weights = newWeights, Bias = newBias, GlobalError = newGlobalError },
}
);
Before I pull it all together, I want to make a small change to the "Output" function - the current version only works if there are precisely two inputs and two weights but the "UpdateWeights" function from a moment ago works with any number of inputs and so I think that "Output" should too. So we'll replace this:
private static bool Output(double[] weights, double bias, double x, double y)
{
var sum = (x * weights[0]) + (y * weights[1]) + bias;
return (sum >= 0);
}
.. with this:
private static bool Output(double[] weights, double bias, double[] inputs)
{
var sum = inputs.Zip(weights, (input, weight) => input * weight).Sum() + bias;
return (sum >= 0);
}
(Note that using "Zip" again means that we don't have to resort to any for loops)
Combining all of this, the network-training code becomes the following:
const double learningRate = 0.1;
var finalResult = Enumerable.Range(0, int.MaxValue)
.Scan(
seed: new
{
Weights = new[] { r.NextDouble(), r.NextDouble() },
Bias = 0d,
GlobalError = double.MaxValue
},
func: (previousState, iteration) =>
{
var resultForIteration = trainingData.Aggregate(
seed: new { Weights = previousState.Weights, Bias = previousState.Bias, GlobalError = 0d },
func: (stateSoFar, pattern) =>
{
var output = Output(stateSoFar.Weights, stateSoFar.Bias, pattern.Item1) ? 1 : -1;
var localError = (pattern.Item2 ? 1 : -1) - output;
return new
{
Weights = UpdateWeights(stateSoFar.Weights, learningRate, localError, pattern.Item1),
Bias = stateSoFar.Bias + (learningRate * localError),
GlobalError = stateSoFar.GlobalError + Math.Abs(localError)
};
}
);
Console.WriteLine("Iteration {0}\tError {1}", iteration, resultForIteration.GlobalError);
return resultForIteration;
}
)
.First(state => state.GlobalError <= 0);
The final piece of the puzzle is to change the "Display network generalisation" code to remove the for loops from there too -
for (double x = 0; x <= 1; x += .25)
{
for (double y = 0; y <= 1; y += .25)
{
var output = Output(weights, bias, new[] { x, y });
Console.WriteLine("{0},\t{1},\t{2}", x, y, output ? "Yes" : "No");
}
}
The natural thing would seem to be to replace those loops with Enumerable.Range calls.. however, "Range" only works int values and we need to use double in order to increment by 0.25 each time. We could write a new "Range" extension method that would take double values or we could just workaround the limitation. If we want the values 0, 0.25, 0.5, 0.75, 1 then that's five distinct values. The number of items may be calculated by taking the end value, subtracting the start value, dividing by the increment and then adding one (to ensure that we get the start value and the end value).
In this case, that would be ((1 - 0) / 0.25) + 1 = 4 + 1 = 5.
We can do that in code like this:
const double startAt = 0;
const double endAt = 1;
const double increment = 0.25;
var range = Enumerable.Range(0, (int)((endAt - startAt) / increment) + 1)
.Select(value => value * increment);
We then want to "cross join" range with itself so that we loop through every (x, y) combination. We can do that with creative use of "SelectMany" -
var xyPairs = range.SelectMany(value => range, (x, y) => new[] { x, y });
And now that nested for-loop may be replaced by this:
const double startAt = 0;
const double endAt = 1;
const double increment = 0.25;
var range = Enumerable.Range(0, (int)((endAt - startAt) / increment) + 1)
.Select(value => value * increment);
var xyPairs = range.SelectMany(value => range, (x, y) => new[] { x, y });
Console.WriteLine(string.Join(
Environment.NewLine,
xyPairs.Select(inputs => $"{string.Join("\t", inputs)}\t{(Output(finalResult.Weights, finalResult.Bias, inputs) ? "Yes" : "No")}")
));
That's the final piece of the convert-to-functional-code puzzle. Now we just need to translate it into F#!
Sidebar: "Function" vs "Method"
I find that in languages that are thought to be object oriented, the words "function" and "method" are commonly used interchangeably. Since beginning to become interested in so-called "functional programming", I've tried to find out whether there is a definitive or accepted difference between the two (after all, it's called functional programming rather than methodical programming, so surely someone thought that there was a difference!).
A few times, I've heard that the difference is that a "function" should not have any side effects and so should always return the same value given the same inputs. On the other hand, a "method" may cause side effects or rely upon ambient references - if the code writes to disk or reads DateTime.Now then it's not "pure" (where "pure" means that it relies only upon its arguments and does not produce any side effects - it only produces a return value and does not manipulate anything else) and so should be described as being part of a method rather than part of a function. Most recently I've seen it described in this Software Engineering Stack Exchange answer.
I try to use the word "function" only when it is known to be a pure function and a "method" otherwise (when it either definitely causes / relies upon side effects or if it's not clear). I still get it wrong from time to time (for example, I've been referring to LINQ "methods" in this post and we can probably presume that they are pure functions in most cases) but I'm still in the process of trying to internalise this terminology while I'm trying to internalise writing a more "functional" style of code for writing F#.
Writing F# code
If you've read this far then you may be detecting an unexpectedly abrupt end to the post judging by your browser's scrollbar!
Originally, I had intended to include all of the above content and go into how precisely to translate the functional C# code into F# but it quickly became clear that the post would be insanely large (I've written my fair share of monster posts in the past and I think that the time has come to put an end to them - this one's already pretty hefty).
Cliffhanger!
Sorry.
My next post will jump straight into F#. I will assume zero prior knowledge of the language itself but I also want to proceed at a decent rate. Hopefully this will mean that you won't get bored if you already have a little exposure to F# (or maybe it will be the worst of both worlds and be too slow for F# novices but too fast for those who've never seen it before). Let's wait and see*!
* (Should you be desperately excited and dying for part two, rest assured that it's already written and just needs a thorough proof-read - so it should be published early next week at the latest)
I'm not sure how many posts there will be in the series in total but the Single Layer Perceptron is just the first model that I want to cover before moving onto the Back Propagation Neural Network model and then onto the Multi-Output variation (which will be necessary in order to classify hand written digits from 0-9 as opposed to being a simple yes/no classifier). Although I said that performance is not my primary concern for this playing-with-F# process, there are a couple of interesting things that I'd like to talk about on that front. So there should be a lot to come over the next few months!
Posted at 22:18
Face or no face (finding faces in photos using C# and Accord.NET)
I've always been intrigued as to how facial detection and recognition is handled by computers. It's one of the few effects that is seen in Hollywood films that seems convincing - where someone is tracked through a city, live CCTV feeds finding their face as they move from one street to the next. For a more mundane example, facial detection has been built into digital cameras and smartphones for quite some time now (my phone puts green squares around faces in photos and, I presume, uses this information to decide where to focus).
I knew literally nothing about the subject to begin with and so I hit the internet and tried to find out everything I could about it. Turns out that there's a lot that's been written about this, with various different methods and approaches discussed and documented. It's an interesting subject because it's been so affected by the rate of change in technology - for example, the digital cameras that introduced it had access to much less processing power than modern day devices do. I've had a hard time finding definitive information about when digital cameras started offering this facility but I'm getting a rough impression that it's over the last ten years (citation needed!) - when you think about how phones, for example, have changed in ten years in terms of their power.. well, it's a lot!
Having said that, digital cameras (and web cams) can take some shortcuts and only concern themselves with subjects that are facing directly towards the camera, since these are more likely to be subjects that are of interest - it's not as important to worry about people looking at ninety degrees from the camera lens, for example). So, straight away, it's apparent there are going to different techniques and different requirements for different situations and some will be more expensive than others.
I suspect that this is going to be an ongoing investigation for me; so far I've only managed to implement facial detection functionality and not facial recognition (once a face has been detected, is it someone from a database of known faces?). I thought I'd present what I have at this point, though - if it's interesting to me then maybe it will be of interest to other people! And I couldn't find much material out there that goes into enough detail that it's reproducible without being a really dense research paper (and certainly not ones that make it easy to reproduce their findings using C#), so I thought that I'd try to fill that gap. There are articles out there about using libraries to do all the hard work for you - but where's the fun in that?! I want to know how the code I'm calling is working.
tl;dr
My current code (github.com/ProductiveRage/FacialRecognition) identifies faces in photos by using two passes. First, it looks for regions of skin that have holes (that we presume may be eyes and a nose) and that are very roughly the right proportions to be a face.
The image content from these regions is passed through a "linear support vector machine", which will have been trained to classify a potential image region as a face or as not-a-face.
Before embarking on this adventure, I had no idea what a "support vector machine" even was. If you don't either then maybe you'll come away from this feeling like you know a little something about machine learning. I know that I did! And "machine learning" is a phrase that I've been interested in finding out more about for quite some time now, it seems like it's cropping up everywhere! I have a strong feeling that trying to perform facial recognition is going to involve even more magical sounding terms - such as "deep convolutional neural network" - but that's going to have to wait for another day, it's one (baby) step at a time for me.
The "Naked People Skin Filter"
In a past life, I worked in IT Support and, one day, I was asked by the Head Clinician why I'd been printing out porn. Which confused me considerably since I had most certainly not been printing out explicit material. There had been complaints about the colour tone and contrast of a new colour laser printer and so I'd sent a full-page test image to it that included greyscale content, colour grids and images that contained a lot of skin. Apparently printing out pictures with lots of skin in it raises eyebrows and maybe it's for similar reasons that a research paper entitled "Naked People Skin Filter" amusingly sounds a touch pervy (or maybe that's just a British thing.. we do love to keep most of our naked-skin-unveiling behind closed doors - because it's so cold!).
This "Naked People Skin Filter" paper was published by Margaret M. Fleck and David A Forsyth and is available at http://mfleck.cs.illinois.edu/naked-skin.html. It essentially describes an algorithm to detect regions of skin in an image. In 1997, another paper "Face Detection in Color Images" described starting with that skin-tone-identifying approach and then using it to try to find solid regions of skin that have a few holes in, on the basis that this is probably a face (where the holes are eyes, nose, mouth).

Note: That "Face Detection in Color Images" link use the Wayback Machine to make available a GeoCities page. Maybe it's a sad reminder that there was actually worthwhile content on GeoCities as well as the many harshly-coloured-and-bizarrely-animated eye-watering monstrosities. By the way, if you (quite rightly, imho) think that the web has lost something by having less places for people to upload content for free then check out NeoCities - it's awesome because it makes that possible again (and all the good and bad that comes with it)!
"Face Detection in Color Images" uses an example image of Tiger Woods and so I will use that same image while I discuss what I've done, based upon these articles.
There are a set of steps that are followed when trying to identify faces in an image:
- Scale the image down (depending upon its size)
- Avoid desaturation by bring colour down values so that the minimum is true zero
- Transform RGB colours into the RG/BY colour space, alongside an Intensity spectrum
- Calculate "texture amplitude" across the image (how quickly intensity changes - the theory is that areas of skin have a relatively low texture amplitude)
- Calculate hue and saturation across the image (in order to identify areas that seem to be skin-coloured)
- Combine the texture amplitude and hue data to identify areas of skin (the texture amplitude, hue and saturation must be within acceptable "this is probably skin" bounds)
- Expand these areas of skin using a more relaxed texture amplitude / hue / saturation "this is probably skin" filter
- Check these areas for holes - no holes (for non-skin facial features, such as eyes) means no face
- Any skin areas that are very small are ignored
- Any skin areas that are extreme aspect ratios are ignored (very, very wide areas or very, very tall areas are probably not faces)
- Expand the areas slightly because, even with the flexible-skin-filter expansions, the area that a human would identify as being a person's face is slightly larger than the areas identified by this algorithm
Calculating hue, saturation and texture amplitude (steps 1-7) to identify skin areas
The first few steps are fairly simple. If the image is either taller or wider than 400px then it's shrunk down so that the largest side is 400px. "Naked People Skin Filter" talks about applying "smoothing" (which I'll cover in a moment) relative to the size of the image but doesn't suggest any restrictions on the image size. "Face Detection in Color Images" mentions that only images up to 250px were used. With the test images I used, I found that capping at 400px provided a reasonable balance between identifying faces and not taking too long to process. I used the Tiger Woods image initially to try to ensure that my calculations were matching those described in "Face Detection in Color Images" but I used other test images (which will appear further down) to double-check that everything seemed to be working as expected. There are some differences between how Fleck & Forsyth ("Naked People Skin Filter") and Kapur ("Face Detection in Colour Images") perform the analysis and my test images led me to tweak a few parameters myself.
Fleck & Forsyth recommend pulling down the colour values so that the minimum value is zero because it "avoids potentially significant desaturation of opponent color values if the zero-response is far from zero". What this means is that the darkest parts of an image are probably not "true black" (ie. RGB 0, 0, 0) and the theory is that we should get better results if everything is adjusted down so that the darkest colour is black. In practice, I look for the lowest of any of the R, G or B values from any pixel in the image and subtract that value from every R, G and B value across all pixels in the image.
Next, I generate "RgByI" values for every pixel. This a trio of values; an RG (red-green) spectrum value, a BY (blue-yellow) spectrum value and an intensity. Since I'm going to spend a lot of time taking the pixels from an image and loading them into a 2D array and then performing a range of operations on them, I've written a DataRectangle<T> class that makes this easier. When I first read the data from an image, the pixels are loaded and used to populate a DataRectangle of RGB values. When I need to get RgByI values from them, I can do the following (using Kapur's formulae from "Face Detection in Colour Images) -
var rgByIValues = colourData.Transform(colour =>
{
Func<byte, double> L = x => (105 * Math.Log10(x + 1));
return new IRgBy(
rg: L(colour.R) - L(colour.G),
by: L(colour.B) - ((L(colour.G) + L(colour.R)) / 2),
i: (L(colour.R) + L(colour.B) + L(colour.G)) / 3
);
});
In order to reduce unhelpful detail in the image somewhat, the RgByI values have a "windowing median filter" applied to them. From "Face Detection in Colour Images" -
The Rg and By matrices are then filtered with a windowing median filter .. with sides of length 4*SCALE. The SCALE value is calculated as being the closest integer value to (height+width)/320
(The "Naked People Skin Filter" paper recommends using 2*SCALE for the RG and BY values, which I have gone with because I found the results to be just as accurate and it's less computational work than 4*SCALE)
To do this, you go through every pixel and take its value and the values from the surrounding pixels, sort them, take the middle value (the "median") and use that as the new value for the current pixel. The idea is that this reduces noise by discarding any outlier pixel colours in a given range. I take a square block around where the initial pixel is but it would probably be better to approximate a circular area if the media filter radius is large (in my filter, it's never more than three).
After smoothing the RG/BY data, their values are combined to generate hue and saturation -
var smoothedHues = smoothedRG.CombineWith(
smoothedBY,
(rg, by) => new
{
Hue = RadianToDegree(Math.Atan2(rg, by)),
Saturation = Math.Sqrt((rg * rg) + (by * by))
}
);

The two images here are the hue and saturation values generated from the original image.
In order to generate greyscale images, I had to translate the hue and saturation values into the 0-255 range. The hue values will be in the range of -180 to +180 degrees so I just added 180 and then divided by 2. The saturation values are always positive and won't exceed 0-255 if multiplied by 2, so I just did that.
Generating texture amplitude is more complicated. We start with the intensity values from the RgByI data. We then run that through a median filter of 2 * SCALE and calculate the difference between every point in the median filter result and the original intensity. Finally, we run the result of the calculation through a median filter of 3 * SCALE. It may be clearer with some code -
var smoothedIntensity = rgByIValues.MedianFilter(
value => value.I,
2 * scale
);
var differenceBetweenOriginalIntensityAndSmoothedIntensity = rgByIValues.CombineWith(
smoothedIntensity,
(x, y) => Math.Abs(x.I - y)
);
var textureAmplitude = differenceBetweenOriginalIntensityAndSmoothedIntensity.MedianFilter(
value => value,
3 * scale
);

(Note that the values 2 and 3 in the above code are much lower than Kapur suggests - 8*SCALE and 12*SCALE - but the median filtering algorithm that I threw together was very slow using the higher values and using lower values - which meant that the processing completed much more quickly - did not seem to affect the outcomes)
Hopefully it's apparent that around the lower face there is low texture amplitude. Texture amplitude is higher around the facial features but that's to expected. There is low texture amplitude elsewhere in the image (particularly in the sky behind him, the texture is very smooth there and so the texture amplitude is very low) but what we're going to look for is areas that appear to be skin in hue/saturation and in texture amplitude.
Now that we have all of the information required to guess whether a given pixel is within the acceptable bounds of "probably skin", we can create a skin mask (a DataRectangle<bool>) -
var skinMask = smoothedHues
.CombineWith(textureAmplitude, (hs, t) => new
{
Hue = hs.Hue,
Saturation = hs.Saturation,
TextureAmplitude = t
})
.Transform(hst =>
{
return (
((hst.Hue >= 105) && (hst.Hue <= 160) && (hst.Saturation >= 10) && (hst.Saturation <= 60)) ||
((hst.Hue >= 160) && (hst.Hue <= 180) && (hst.Saturation >= 30) && (hst.Saturation <= 30))
)
&& (hst.TextureAmplitude <= 5);
});
This is another point at which I have added my own tweaks to the processing. There are slightly different ranges of acceptable hue / saturation / texture amplitude suggested by Fleck & Forsyth than are suggested by Kaypur and I found that I wanted to change them a little based upon the test images that I was using.

The final step in generating the skin mask is to try to identify any skin areas just outside the identified mask. I've used the approach suggested by Kapur, who recommends it because it "helps to enlarge the skin map regions to include skin/background border pixels, regions near hair or other features, or desaturated areas".
The idea is that we look at negative values in the DataRectangle<bool> skin mask and check whether any of the adjacent values is positive and if the colour of the pixels that resulted in the false value passes a more relaxed skin filter. The relaxed skin filter test demands only that the hue is within the range 110-180 and that the saturation is with 0-180 (the text amplitude is not considered). This expansion work is performed twice.
Recognising skin objects (and checking for holes)

In order to get back some of the details that are within the skin mask areas, the original image is changed to greyscale and then the skin mask is combined with it to produce a new skin mask that is slightly more restrictive; any negative content from the skin mask remains negative while positive content is only allowed if the greyscale intensity is within an acceptable range. Everything from this point (including this step) comes from the "Face Detection in Color Images" article, since "Naked People Skin Filter" ends when the skin regions are detected (it has no interest in faces, specifically).
skinMask = colourData.CombineWith(
skinMask,
(colour, mask) =>
{
if (!mask)
return false;
var intensity = colour.ToGreyScale();
return (intensity >= 90) && (intensity <= 240);
}
);
In order to turn this DataRectangle<bool> mask into groups of points (where each group represents a distinct area of skin), I used a variation of the "Stack based implementation" from this article: Flood Fill algorithm (using C#.Net). If you're looking my code, it's the "TryToGetPointsInObject" method in the FaceDetector.cs class. I'm not stressing out about performance at this point, I just wanted to get things working and then considering measuring & improving in the future - so finding a nice simple flood fill algorithm was very helpful (I'm not saying that it's not a well-performing method, I'm just saying that at this point in time it's not critically important to me one way or the other).
Any skin objects that are very small (have less than 64 * SCALE points) are ignored. What is slightly more complicated is to identify any completely enclosed holes in the skin object. But it's not much more complicated - the basic approach is, for each skin object, take a negative point within the bounds of the skin object and use the flood fill algorithm again; if the fill reaches the edges of the bounds then the negative point was not part of an enclosed hole. Then move on to the next negative point within the bounds that hasn't already been included in a flood fill operation and continue doing this until a fully enclosed hole is found that's larger than a given size (1 * SCALE).

With the Tiger Woods image, we could actually stop here. It successfully identifies only his face as a possible face region. However, with other test images I used, some more work was required. I found that I could quite easily eliminate a few false positives by ignoring any regions that were obviously the wrong aspect ratio (either very long and shallow sections or very tall and narrow sections). I also found that, depending upon lighting or what background a face was against, sometimes the detection process up to this point would result in a region that is too tight over the facial features - expanding the matched area a little meant that the next filtering in the next stage would get better results.
The real problem, though, is false positives - the algorithm will often identify areas that are not faces.
Applying this to other images
I wanted to try applying this facial detection logic to some other images. I'd used the image from one of the articles so that I could try to produce intermediate images that looked similar to those in "Face Detection in Color Images" so that I could reassure myself that I was (at least approximately) doing things correctly as described. But now I wanted to try it on some other test images.
In my Pictures folder, some photos from an Easter weekend* night out I went to a couple of years ago jumped out at me. Initially, I only used them because they made me laugh but, on closer inspection, they're actually really useful for illustrating what the skin tone detection process (and the subsequent support vector machine classification) is good at and where their limitations come into play.
* (which goes some way to explaining the eggs and the costumes.. the photos were put up on Facebook by a professional photographer, I hope he doesn't mind me reproducing them here - I tried getting in touch to ask but he didn't get back to me)

Firstly, we have this fine gentleman. The skin tone pass has identified his face perfectly but it's also misidentified two regions that contain colours and textures that the skin filter allows through.

Looking at the generated skin mask (where each distinct skin object is filled with a different colour), it should be clear why this has happened.

If we take another photo then another problem is apparent - with this group of people, there are lots of enclosed skin objects that have holes in that are being identified as faces but that are actually hands holding things.
Also, because we ignore regions that are very small, there is a limit to what faces the skin tone filter will identify. If you look closely at the group photo there is an undetected bearded face along the left edge (near the top) but I am happy for it to exclude him since I think that it is a reasonable compromise to prefer faces that are in the foreground. On the whole, it does a good job of detecting faces but it may also produce a lot of false positives.
So the next step is to try to find a way to filter these regions down further, to try to get rid of those pesky false positives. To do this, I went back to the internet. One of the pages that I found incredibly useful was the "HOG Person Detector Tutorial" by Chris McCormick. He introduces a popular and modern technique, touches on its history and then goes into an illustrated explanation of how to implement it. It's almost redundant me going over it again! .. but it's my blog and I'm talking about how I implemented it, so I'm going to start from the beginning anyway :)
At the very highest level, what we're going to do is this -
- Take a load of images that are known to be faces and a load of images that are known to not be faces - these sets of "positive" and "negative" images are our "training data"
- Extract a load of numbers from each image - each image must be processed in a manner that results in them each producing the same amount of numbers (this is called "feature extraction")
- The resulting data (which is a big list of entries, one from each training image, where each entry is a list of features from that image and a boolean value for whether the image was a face or not) is used to train a "Support Vector Machine" (which I'll explain in a second)
- Now that we have a trained SVM, we can use the same feature extraction process from step 2 on each of the sub-images generated by the skin tone detection process and the SVM should tell us whether each one is a face or not a face
So what is a Support Vector Machine?
This is a concept that I had never heard of before, so I know first-hand what it's like trying to search around on the internet for a good description. The problem is that a lot of articles seem to be aimed at people who know at least something about machine learning and they go immediately to showing lots of formulae and talking about techniques that I'd never heard of. One example is "Kernel Support Vector Machines for Classification and Regression in C#" by César Souza (who wrote much, if not all, of the Accord.NET library - which I will be using later); this is a really well-written article that I appreciate now but it was on my "come back to this when you know more" list for quite a while after I first found it!
So I'm going to take a real beginner approach and try to describe it in a manner that would have helped me a few weeks ago.
Firstly, an SVM tends to be a "binary classifier". This means that it will be trained with data that is all categorised as either yes or no. After it has been trained, you may only ask it to classify further data as being a yes-or-no result. (Actually, there is a such a thing as a "Multi-Class Support Vector Machine" that can return a greater range than binary but it's not relevant here so I'm going to forget about it for now).
(Time for some graphs. Shout out to Create your own XKCD-style Graphs, which helped me come up with what's below!)
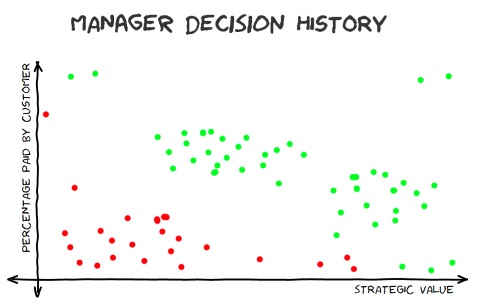
To conjure up an example that almost sounds feasible, imagine that every development task at a software shop requires that its strategic benefit to the company be quantified, along with the percentage of the work that a customer is just dying to pay in order for it to be done (presuming that there is a customer who wants it and that it's not just a task for internal purposes). Since every task needs to have these pieces of information before your manager will decide whether or not the work will be scheduled, there exists historical records of estimated tasks which have two "features" (strategic value and percentage-that-will-be-immediately-paid-for-by-customers) and an outcome of either "yes, it was done" or "no, we didn't do it".
If something is of high strategic value to us and it happens to be a feature that a customer is chomping at the bit for (and so will contribute significantly towards) then it seems like a dead cert that we should do it. Unfortunately, this is not a very common case.. More often, a customer will want something that is important to them specifically. This may not be something that is necessarily very easy to resell to other customers (which would give it more strategic value) or something that will help us deal with internal issues, such as scaleability or technical debt (developments that do help with those will also have higher strategic value).
It seems like there's a roughly linear correlation between a development's strategic value, the fraction that customer(s) are willing to immediately pay for it and whether the work got the go-ahead. It's like we could draw a line and everything above it tends to get the green light by our manager and everything below it gets rejected.

An SVM is (according to wikipedia), a:
"model with associated learning algorithms.. An SVM model is a representation of the examples as points in space, mapped so that the examples of the separate categories are divided by a clear gap that is as wide as possible"
What this boils down to is that we're essentially trying to come up with a formula to split those two sets of points. Then, when we get a new feature-pair (strategic value vs amount-customer-will-pay) we can plug those two numbers into the formula and work out which side of the line we're on (where one side means I-predict-yes and the other side means I-predict-no).
The hard work in the machine learning algorithm is working out where that line should go. Ideally, you want all historical "yes" results on one side and all historical "no" results on the other side. In some cases, though, this is not possible and there will be some outliers (remember that task that you had to do that seemed to have no strategic value, that no customer was willing to pay for and yet someone at one of those customer companies had convinced one of your directors to do it at as a favour...?). Whether there are any outliers or not, there are probably still many slight variations on what line could be drawn. It's common for an algorithm to try to arrange the line so that it is equally distant from the positive results as it is from the negative results but there are some variations on this theme. This is really what the magic is in this process - giving the computer the results and letting it find the best match.
Higher dimension planes and non-linear methods
In the above example, each data point only had two features which made it very easy to envisage on a 2D graph how they related to each other (which isn't surprising since it's an example I made up to illustrate that very point!). Sometimes, though, more data is required. It could be that you plotted strategic-value against amount-customer-will-pay and could see no correlation, though one was there - but hidden due to the interaction of another feature. Imagine if you find historical data that shows that a customer wanted to pay for a new feature and the feature was of reasonable strategic value but it wasn't authorised. Or if there were a bunch features with comparatively low value that did get the go-ahead. And if you realised that these were not outliers and that lots of results looked to be "all over the place". Well, it could be that the reason that the high value work wasn't done was because the development team were already stacked out with important work. Whereas those low value jobs that did get done happened to come in during quiet periods where they could be easily slotted into the schedule. This would mean that there was actually a third factor at play; available developer resources.
What would be required to model this would be to include some quantified "available developer resources" value with each data point. With this additional information, we should be able to construct a useful prediction model. However, the points could no longer be plotted on a simple 2D graph - now they would have to be plotted in 3D space. And so the formula that would be produced from the training data would no longer draw a simple line, it would have to describe a plane that cuts through the 3D space (with the "yes" values on one side and the "no" values on the other).
If you had more than three features to each data point then you would no longer be able to draw a graph of it, your points would now live in the mysterious-sounding "n-dimensional space". It's still possible to concoct a formula that divides the data point within that space, it's just not very easy to imagine it in a visual manner. On the 2D graph, it was a one-dimensional line that split the data points and allowed us to make predictions against future data points. On the 3D graph, it would be a two-dimensional plane that divides the points. In n-dimensional space, it will be a "hyperplane" (which just means that it is a structure with one less dimension than the space that it exists in). Once you start throwing terms around like "Linear SVM" and "hyperplane", it's hard not to feel like you're making real progress towards getting a handle on all this machine learning lark! I mention these higher dimensional spaces, though, not just because they sound exciting but because they will be relevant soon..
Something else that's interesting when considering SVMs is that, even with all of the required data, it still might not be possible to delineate the positive and negative results with a linear formula. If we go back to imagining a 2D graph, there could be curious curves in the data that are predictable but can not be cleanly cut with a straight line. In this case, we would have two choices - have the algorithm try to find a line that cuts the results as well as possible (but accept that this will have a lower accuracy because we know that a straight line will get a lot of predictions wrong, based upon the data we've got) or we can allow it to try to come up with a non-linear separation.
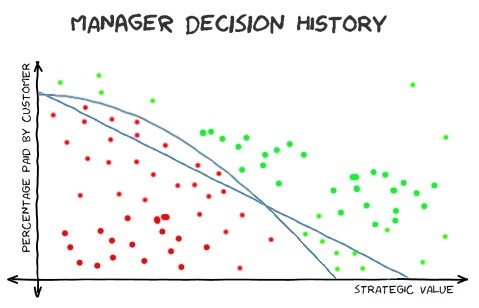
If, say, you had a manager who leant more towards authorising tasks that had greater strategic value, even if there weren't immediately customers to finance the work (maybe they favour tasks that improve efficiency for work that customers are excited about or maybe it's to lay the groundwork required before customer-led work can continue) then it might not be possible to perfectly fit a straight line to the data. One option, when trying to model this, would be to specify that the learning algorithm could use a non-linear kernel, would would hopefully generate better predictions. Or you could stick with the linear approach and accept that it will be less accurate. Looking at the graph here, there is a curved line that matches the data precisely and there is a straight line that tries its best but can't help splitting the data so that some negative values are above the line (where only positive values should be) and some positive values are below the line (where only negative values should be).
This is another illustration that machine learning can't perform miracles. Before, I described an example where a third feature would need to be added to the data ("available developer resources") - without which it would be impossible to train a useful model. Here, we can see that sometimes we need to have some insight into what prediction models may or may not work for us (ie. we need to know that a linear kernel won't yield the best results).
I'm not going to dwell on this any longer here because, happily, a linear SVM is a good fit for the data that we'll be working with for classifying face / not-a-face. I don't think that I yet understand enough about the subject to explain why a linear model works so well for what we want to do but I do have links to articles (which I'll include at the end of this post) that seem happy to explain why this is the case.
Feature extraction for maybe-a-face images
So, if an SVM can be trained on pre-existing data and then used to decide whether other data (that it's never seen before) should be classified as a yes or a no, how can this be applied to our "potential face regions"? The first thing that we need to do is decide how to extract features from an image. In the "Manager Decision History" examples above, there were only two or three features but there's nothing stopping us from extracting many more features from our inputs. Whatever we do, though, we need to generate the same number of features for every input into the SVM - so we'll almost certainly have to resize each maybe-a-face sub-image before processing it. We could consider taking all of the pixel data from each resized sub-image (every red value, green value and blue value from every pixel across the entire sub-image).. but we're not going to. Not only would there be a lot of data to work with, there would also be too much variance introduced by the environment of the source photograph. We want to try to give the SVM meaningful data for it to analyse and remove irrelevant variables where possible. By "irrelevant variables", I mean that it would be great if we could ignore the lighting in an image and focus on the shapes.
Sometimes the lighting varies not just from one image to another but within the same image - if there is a person outside and sunlight falls on one side of them, for example. And it would be great if we could ignore the contrast and the shades of colour - if you can imagine fiddling with an image in Photoshop (or the excellent Paint.NET), recolouring an image or playing with the contrast and brightness doesn't affect your ability to recognise what's in the image (unless you really stretch some of those dials to the max) and we don't want those sorts of differences to have any impact on the SVM's predictions. What we really want is to discount as much of this variance as possible when preparing the inputs (both the inputs used to train it and the subsequent inputs that we want predictions for).
A method that works well to achieve this is to generate normalised "Histograms of Oriented Gradients" from the sub-image. Again, I've come to this conclusion from doing a lot of reading around and then attempting to implement described methods to see how they work - I'll include references to articles with more details at the end of this post.
The premise is fairly simple, you need to:
- Ensure that every image to process is a consistent size before starting (if an image is the wrong aspect ratio for whatever the "consistent size" that you decide on is then add some black bars above-below or left-right, depending upon which sides are too long/short)
- Greyscale the image
- For every pixel, work out the direction that the intensity of light on the image is changing and how quickly it's changing
- Split the data into blocks
- Reduce each block into a histogram of gradients
- Apply some sort of normalisation to reduce impact of contrast or brightness differences from image to image
- Use the resulting data as the image's feature set in the next step!
I think that steps 3 and 5 are probably the ones that require further explanation. Since we have a greyscale image by step 3, instead of colour data we effectively have "intensity" values for each pixel. To work out the angle in which the intensity is changing, take the intensity of the pixel below the current one and substract it from the intensity of the pixel above the current one. This is the "y difference" - or "delta y", so I'll name it "dy" (so that I can sound all maths-y). "dx", as you can probably imagine, is the difference between the intensity of the pixel to the right minus the intensity of the pixel to the left. We can calculate the angle at which intensity is changing (and how big the change is) with the following:
var angleInDegrees = RadiansToDegrees(Math.Atan2(dx, dy)));
var magnitude = Math.Sqrt((dx * dx) + (dy * dy));
Note that "Math.Atan2" returns a value in radians. Radians are another unit of measurement of angles but instead of describing a full circle by going from 0-360 degrees, the scale goes from 0-2π radians. So, to convert from radians into easier-to-deal-with-in-this-case degrees we can do this:
private static double RadiansToDegrees(double angle)
{
return angle * (180d / Math.PI);
}
Also note that Atan2 actually returns values in the range of -π to +π and so calling RadiansToDegrees on the result will give us a value from -180 to +180.
(When calculating gradient angles and magnitudes, any pixels on image edges won't have pixels surrounding in every direction and so I just record them as having both an angle and magnitude of zero)
Now for step 5, we want to produce "histograms of oriented gradients" (one for each block that we've split the image into in step 4). I always envisage a histogram like a bar chart - it shows how values are distributed across a range.
(The example on the left is from wikipedia and reproduced here under the creative commons license)
To generate our histograms, we want to assign the gradients with the block across nine buckets, spaced twenty-degrees apart. The first will be at 10 degrees, the second at 30 and they'll go all the way up to 170.
We're going to use "unsigned gradients", which means that if we have a gradient where intensity is changing only vertically, we don't really care if it's getting brighter as it goes down or brighter as it goes up, we only care that the line is precisely vertical. Similarly, imagine the intensity increasing up-and-right, at 45 degrees - we're happy to treat this the same as intensity going in precisely the opposite direction; down-and-left and 225 degrees (or -135 degrees since our current angleInDegrees values are in the -180 to +180 range). What this essentially means is that we want to tweak our angles so that they are all within 0-180 (instead of -180 to +180). To do, so we just add 180 degrees to any values less than zero.
Every gradient needs to be assigned to one or more of these buckets. If a gradient's angle is precisely 10 degrees then the entirety of the gradient's magnitude is added to the 10 bucket. However, if it's between 10 and 30 then its magnitude is split proportionally between 10 and 30 (so a gradient of 20 degrees is split evenly between 10 and 30 while a gradient of 25 degrees will contribute 3/4 of its magnitude to the 30 bucket - which it is 5 degrees away from - and 1/4 of its magnitude to the 10 bucket - which it is 15 degrees away from).
Performing this transformation on the image is an effective way of reducing the amount of data that we need to deal with. If we decide that the standardised size of the images that we want an SVM to classify is 128x128 then we 128 x 128 x 3 = 49,152 values (since every pixel has three colour values; red, green and blue). If use a block size of 8 when generating the HOG data then the 128 x 128 image will be 16 x 16 blocks and each block has 9 values (since each histogram has values in nine bins), which gives a total of 2,304 values.
Another nice thing about this representation of the data is that, if you sort of squint, you can kind of make out the shapes that were in the source image -

If you get curious and want to try generating HOGs for your own images, there is code in my my GitHub project to do this..
using (var image = new Bitmap(imagePath))
{
using (var resizedImage = new Bitmap(image, new Size(128, 128)))
{
// (Can ignore GetFor's return value when only interested in generating a preview image)
FaceClassifier.FeatureExtractor.GetFor(
resizedImage,
blockSize: 8,
optionalHogPreviewImagePath: "HOG.png",
normaliser: GlobalNormaliser.Normalise
);
}
}
.. which brings me neatly on to HOG normalisation (since there's a mysterious reference to a normaliser in the code above). When the gradient magnitudes are calculated, some images may have many pixels that vary wildly in intensity from their neighbours while other images may have smoother, gentler gradients. In both cases, it is the relative flow of intensity that is important, since that helps identify the shapes. If you took an image and produced HOG data for it and then increased the contrast of the image and re-processed it, you would get greater gradient magnitude values in the increased-contrast version of the image, even though they both - so far as we are interested (in the context of trying to detect faces) - contain exactly the same information.
What we want to do is to align all of the magnitudes to a common base line. A simple (and fairly effective) way to do this is to find the largest value of any of the buckets across all of the histograms generated for an image and to then divide every magnitude by this value. In the example above, the 128x128 input image is transformed into 16x16 blocks, each of which is a histogram that contains 9 values. So we get the largest value from each of those 16x16x9 values and then divide all of them by it. This means that the largest value is now precisely 1.0 and every other value is somewhere between zero and one. This is what the "GlobalNormaliser.Normalise" delegate in the code above does. All it essentially has to do is this:
public static DataRectangle<HistogramOfGradient> Normalise(DataRectangle<HistogramOfGradient> hogs)
{
if (hogs == null)
throw new ArgumentNullException(nameof(hogs));
var maxMagnitude = hogs.Enumerate()
.Select(pointAndHistogram => pointAndHistogram.Item2)
.Max(histogram => histogram.GreatestMagnitude);
return hogs.Transform(hog => hog.Multiply(1 / maxMagnitude));
}
However, there is a variation on this that has been found to produce more accurate results; "block normalisation". The original description of this process comes from (as I understand it) the original research into using HOGs for this form of detection ("Histograms of Oriented Gradients for Human Detection [PDF]") -
For better invariance to illumination, shadowing, etc., it is also useful to contrast-normalize the local
responses before using them. This can be done by accumulating a measure of local histogram “energy” over somewhat larger spatial regions (“blocks”) and using the results to normalize all of the cells in the block
What this means in practical terms is explained well by one of the articles that I linked earlier ("HOG Person Detector Tutorial"). In essence, it means that we can get better results from normalising over smaller areas of the image. Instead of taking the max magnitude across the entire set of data, the idea is to group the histograms into blocks of four and normalising over those.
Let's go back to Tiger Woods' face to illustrate what I mean.


We first take the 2x2 histograms from the top left of the image - we get the max magnitude from within those four histograms and use it to normalise the values within them. These four normalised histograms will provide the first sets of values that we extract from the image.
Then we move across one to get another set of 2x2 histograms and repeat the process; get the max magnitude from within those four histograms, use it to normalise them and then take those four normalised histograms as the next set of values that we have extracted from the image.
What you might notice here is that, as we look at the 2x2 blocks of histograms, some of them will appear multiple times. The histograms from the edges of the image won't but the others will. In the Tiger images here, you can see that the two histograms at the right hand side of the block in the first image are included again in the second image (now they are the two histograms on the left hand side of the block).
This means that this "block normalisation" process will result in more data being produced. When we "globally normalised" the HOGs then we had 16x16x9 = 2,304 values. However, if we block-normalise (using blocks of 2x2) then we generate 30 blocks across (there are two edge blocks that are only counted once but the other 14 blocks are all counted twice, so the total is 2 + (14*2) = 30). For the same reason, we will generate 30 blocks worth of data as we go down the image. This means that we end up with a total of 30x30x9 = 8,100 values.
To extract those features, we would tweak the code from before -
const int inputWidth = 128;
const int inputHeight = 128;
const int blockSizeForHogGeneration = 8;
const int blockSizeForLocalNormalisation = 2;
IEnumerable<double> features;
using (var image = new Bitmap(imagePath))
{
using (var resizedImage = new Bitmap(image, new Size(inputWidth, inputHeight)))
{
var blockNormaliser = new OverlappingBlockwiseNormaliser(blockSizeForLocalNormalisation);
features = FaceClassifier.FeatureExtractor.GetFor(
resizedImage,
blockSize: blockSizeForHogGeneration,
optionalHogPreviewImagePath: null,
normaliser: blockNormaliser.Normalise
);
}
}
(Note that I'm setting "optionalHogPreviewImagePath" to null so that "FeatureExtractor.GetFor" doesn't generate a "HOG preview" image - this is because it's much harder to recognise the shapes that the gradients were extracted from when this form of normalisation is use since most of the HOGs appear multiple times, so the preview images are of less interest)
When I tried comparing the results of global normalisation vs block normalisation, I found that I got better result (ie. better accuracy) when using block normalisation, just as the authors of "Histograms of Oriented Gradients for Human Detection" did. The number of images that I've been testing with is, I'm sure, much smaller than the number used by Dalal and Triggs in their research but it was gratifying that I could see improvements with my data set from using block normalisation - if only because it reassured me that I was moving in the right direction!
Training an SVM
It's really coming together now. We've got a way to extract data from an image that we will be able to pass to an SVM in order for it to classify the image as "face" or "not face". There's just one thing that we're missing.. a trained SVM. Or, another way to look at it, two things we're missing - a mechanism to train an SVM and the data to train it with.
Let's start with a general way to train an SVM. For this, I'm going to use a package called Accord.NET. It's a library entirely written in C#, which was a plus to me because I like to see how things work and when I was doing my early reading around on the subject of face detection/recognition, a lot of people were recommending OpenCV. This is a C++ library (which can be called by C# using a .NET wrapper called Emgu), while I would be happier with C# source code that I could more confidently dig around in. (Also, I'm toying with the idea of trying to port some of this work to a Bridge.NET project so that I can try making it work in the browser - this wouldn't be possible if I took a dependency on a library like OpenCV).
Accord.NET really does make it easy.. once you know where to get started. There are a lot of examples on the accord-framework.net site and on the GitHub wiki, though some of the code samples are out of date and will generate compile warnings if you try to use them directly. (Having said that, the warnings can be ignored and it's not too hard to find other examples that compile without warnings - and, from reading some of the GitHub issues, I know that César is aware that some of the docs need updating and is intending to do so when he can make time).
To demonstrate, let's revisit the "Manager Decision History" example from earlier. We'll formulate some example data where we pretend that the Manager is super-consistent and will always authorise work if the percentage that the customer will pay for immediately (as a value between 0 and 1) plus the strategic value (also somehow quantified as a value from 0 to 1) add up to more than 1. (So strategic value 0.9 plus customer-will-pay-immediately 0.2 will be authorised as 0.9 + 0.2 > 1 but strategic value 0.8 with customer-will-pay-immediately of 0.15 will not be authorised as 0.8 + 0.15 < 1). We can then use that data to train an SVM and then try other values against the model -
// Make up some data (in the real world we'd use some proper pre-classified training
// data but this is just an example to demonstate how to train an SVM using Accord.NET)
var decisionHistory = Enumerable.Range(0, 10).Select(x => x / 10d)
.SelectMany(x => Enumerable.Range(0, 10).Select(y => y / 10d).Select(y => new
{
StrategicValue = x,
ImmediateCustomerContribution = y,
Authorised = (x + y) > 1
}));
// From the data, extract the input features (strategic-value and amount-customer-will-
// pay-now)..
var inputs = decisionHistory
.Select(decision => new[]
{
decision.StrategicValue,
decision.ImmediateCustomerContribution
})
.ToArrary();
// .. and the true/false outputs for each of those sets of features
var outputs = decisionHistory.Select(decision => decision.Authorised).ToArray();
// Then use the inputs and outputs to train an SVM
var smo = new SequentialMinimalOptimization<Linear>();
var svm = smo.Learn(inputs, outputs);
The SequentialMinimalOptimization defines the process by which it will be decided when the best match has been found for the data that it's been provided. We're specified that a linear kernel be used, which means that we're presuming that it will be possible to neatly classify our data with a straight line.
Now that it's been trained, we can ask the SVM to predict an output by calling its "Decide" method and giving it a pair of values -
var easyWin = svm.Decide(new[] { 0.81, 0.79 });
This returns true - which is what we would expect since the numbers indicate a feature that has high strategic value (0.81) and there are customers who want it so much right now that they are already getting their chequebooks out (the customer-will-immediately-pay value is 79%).
var lowPriority = svm.Decide(new[] { 0.26, 0.14 });
This returns false - which we'd also expect, since the numbers indicate a feature of low strategic value and one that no customer is excited about contributing much towards the development cost of.
Time for another gotcha. We saw earlier that a linear kernel is not always going to be capable of perfectly classifying the results in the training data. Sometimes you might need to use a non-linear kernel (or stick with a linear kernel but accept a lower accuracy). I didn't talk about what other kernel options there are (because it's not relevant to what I want to do here) but it was an important point that machine learning will sometimes need some external insight in order to be as effective as it can be. Another example of this is that sometimes you need to tweak the training parameters, depending upon the data that you're using. In the below example, I'm going to try to train an SVM in a very similar manner to what we just looked at, but with much less data -
var decisionHistory = new[]
{
// Strategic wins
new { StrategicValue = 0.95, ImmediateCustomerContribution = 0.1, Authorised = true },
new { StrategicValue = 0.85, ImmediateCustomerContribution = 0.2, Authorised = true },
// Customer wins
new { StrategicValue = 0.15, ImmediateCustomerContribution = 0.9, Authorised = true },
new { StrategicValue = 0.2, ImmediateCustomerContribution = 0.9, Authorised = true },
// Everybody is happy
new { StrategicValue = 0.8, ImmediateCustomerContribution = 0.8, Authorised = true },
// Low priority
new { StrategicValue = 0.2, ImmediateCustomerContribution = 0.1, Authorised = false },
new { StrategicValue = 0.4, ImmediateCustomerContribution = 0.2, Authorised = false }
};
var inputs = decisionHistory
.Select(decision => new[]
{
decision.StrategicValue,
decision.ImmediateCustomerContribution
})
.ToArrary();
var outputs = decisionHistory.Select(decision => decision.Authorised).ToArray();
var smo = new SequentialMinimalOptimization<Linear>();
var svm = smo.Learn(inputs, outputs);
The training data is very similar to before in that all authorised decisions still have a feature sum of more than 1 and all rejected decisions have a sum of 1 or less. However, something seems to have gone wrong because when I ask the trained SVM what it thinks of the "lowPriority" example -
var lowPriority = svm.Decide(new[] { 0.26, 0.14 });
.. it returns true! This is not what I want.
The only way that this could happen is if the prediction model that has been generated is completely wonky somehow. To put this to the test, I'm going to use a mechanism that Accord has where you can double-check your trained SVM by running the training data back through it to see how well the prediction model managed to fit it. This can be useful in cases where you're not sure if the SVM kernel that you're using is appropriate, since it can highlight a badly-fitting model. To calculate the error rate when the training data is passed back through the SVM, do the following:
var predicted = svm.Decide(inputs);
var error = new ZeroOneLoss(outputs).Loss(predicted);
This just uses the model to calculate a prediction for each of the inputs and then compares the results to the expected values (then it works out what proportion are incorrect). In this case, the error rate is 0.2857142857142857, which is 2/7. Looking at the predicted values (an array of bool), every value is true! This isn't right, the last two inputs (the "low priority" data points) should result in a false prediction. I guess that that explains why the "lowPriority" example returns true from this model - it seems to return for everything!
We know that a linear model will fit this data because we know that it's a straight line on a graph that separates everything above 1 (which are "decision authorised" results) from everything else (which are "decision rejected" results). So it's not the kernel that's the problem. The only other thing to do is to look for some options to fiddle with. Poring through the documentation, one that sounds promising is "Complexity" (also referred to as "cost") -
The cost parameter C controls the trade off between allowing training errors and forcing rigid margins. It creates a soft margin that permits some misclassifications. Increasing the value of C increases the cost of misclassifying points and forces the creation of a more accurate model that may not generalize well.
That description makes it sound like a bad thing to try increasing the complexity, I think I want a model that will generalise well. However, leaving the complexity at its default is clearly not working well for us in this case. So, I tried changing the SequentialMinimalOptimization initialisation to:
var smo = new SequentialMinimalOptimization<Linear> { Complexity = 10 };
.. and re-running. This time, the predicted array precisely matched the output array, which means that the error rate is now zero. When I ask the new model to predict a value for the "lowPriority" features, it returns false - which is much better!
I've only experienced this problem when working with small amounts of data. To train a face classification SVM, we're going to throw a lot of training data at it and so this shouldn't be a problem (there will be no need to fiddle with Complexity or any other settings). I only mention it now in case you decide to do a few experiments of your own and fall into the same trap that I did!
Training data for faces
We have all the tools that we need now, the final piece of the puzzle is that we need training data to teach an SVM what looks like a face and what doesn't.
I could take the pictures that I found on my computer, run them through the skin tone face detector, manually categorise each maybe-a-face region and then use that information to train an SVM. I would use the HOG feature extractor to generate the training inputs and the list of output values would be the manual classifications that I would have to prepare (eg. sub-image-1 is a face, sub-image-2 is not a face, etc..). This should result in an SVM that could them tell apart each of the sub images automatically. However, that would be cheating! What I want to do is train a classifier with one lot of data and then use the SVM on my Easter Weekend photos to prove that it's worked. (Testing an SVM using the same data used to train it is a bit pointless, it gives you no indication whether you have produced something that is useful for general purpose or if you've only succeeded in training an SVM that is specialised and only works with that particular set of inputs).
It's crucial to train it using both positive images (ie. face images) and negative images (non-face images), otherwise the SVM will have no idea to classify. If, for example, you tried to train an SVM using only positive images then all you teach it is that everything is a positive image! (By always returning true, it would produce a zero error rate for the training data but it's not very useful to alway returns true when trying to classify real work data). So we need both kinds of input and I think that we ideally want to have an equal number of positive and negative images.
(If I had to really think about it, maybe it should be the case that we want at least as many negative images as positive as there are only so many variations of a face that exist but there are loads of things that aren't faces.. however, an equal number of positive/negative has worked well for me and so I haven't felt the need to experiment with different ratios)
I've found various places that have databases of images of faces but I found it difficult to decide how to get a set of negative images. I'm sure that in some things I read, people spoke about using images of scenery.. but I can't see why there should be any particular kind of negative image (such as scenery) that should be used - it could be anything (so long as it's not a face)!
What I did in the end was download the "Caltech 10,000 Web Faces" data set, which includes lots of photos downloaded from various Google image searches along with a text file that, crucially, has coordinates of the faces in the photos. From this data set, I extracted the faces from images but also extracted other parts of the images at random that didn't contain faces. For each face entry in the "Ground Truth" text file, I extracted three images - one where the edges of the sub-image were close around the face and then two where there was a little more background around the face. This should help produce an SVM that can recognise faces when the region around the face is very tight and when it's less so, which is important for classifying the skin tone face detection results - Tiger Woods' detected-face-region is quite tight while the other photos show that much looser face regions may be identified for other photos.
There's no exciting implementation details here. The "CalTechWebFacesSvmTrainer" class is given a bunch of configuration options: path containing the CalTech web face images, path to the Ground Truth text file (which lists all of the face regions in the images), standard size of image to use to generate SVM inputs (128x128), block size for HOG generation (8), normaliser (the OverlappingBlockwiseNormaliser we saw earlier, with block size 2) and number of training images to process. These options will train an SVM on positive and negative images from the Caltech data set and the "TrainFromCaltechData" method will return an IClassifyPotentialFaces implementation, which wraps the SVM and exposes has a single method -
bool IsFace(Bitmap image);
Now, we can take the possible-face sub-images identified by the skin tone pass and pass them to "IsFace". This method will resize the specified Bitmap to the standard image size that the SVM requires, generate normalised HOG data from it and then query the SVM - which returns the final result; is this or is this not a face?
The only configuration option that I haven't mentioned until now is "number of training images to process". We saw before that trying to train an SVM with very little data can be ineffective (unless you know what kernel settings to fiddle with) but it's very difficult to come up with a hard and fast rule of how much data is enough to train from. I think that the best thing to do is just to experiment. My gut told me that it would surely have to be at least 100s or 1000s of images since the SVM has to be trained to classify many variations of faces (and not-faces) and each of the inputs has a lot of values (8,100 - as we calculated earlier) and so it seems like it's going to need to have a lot of information at its disposal so that it can work out what is and isn't important.

So, initially, I tried specifying 500 training images, which resulted in an SVM that actually did a pretty good job. The group photo shown before had all of the maybe-face regions correctly classified (the faces were all identified as faces and the hands in the photos were all correctly classified as not-faces).
However, there was a problem with the image shown here (the problem, btw, clearly isn't the moves being thrown on the dancefloor, since they look like the very essence of poetry in motion). The problem is that one of the maybe-face regions identified by the skin tone pass has been mis-classified by the SVM as a face, when it's really an arm.
(Note that there are some faces in the background that were not identified by the skin tone pass, but I'm not worried about that - it is to be expected that they would be ignored because they are small, relative to the size of the image.. though it should be possible to tweak the skin tone filter parameters if you wanted to try to capture background faces).
Increasing the number of training images to 1,000 didn't address the problem with this particular image and, in fact, made another image worse (where a non-face region was correctly classified as not-a-face before, with 1,000 training images the SVM thought that it was a face). Increasing to 1,500 training images corrected the classification of the dancing image regions but there were still false positives in other images. Such as this one of that same individual who appears to now be wearing a flag (which reminds me of a scene from Fear and Loathing in Las Vegas).

2,000 training images seemed to be the sweet spot. The classifier produced the correct results for every case that I expected it to.
The quantity of training data is going to vary from application to application and will depend upon what sort of feature extraction logic you are using. I think that it makes sense to start with lower quantities, if only because it's faster to train an SVM with less data and you can experiment more quickly with the other variables. To illustrate, on my computer (with the code as it currently stands, which is in a completely unoptimised state, but running a release build) it takes 17s to load the 2,000 images and extract the features from them, it then takes 27s to train the SVM on them. With 500 images it takes 5s to load the image data and 2s to train the SVM. With 5,000 images it takes 42s and 168s.

There's one final tweak that I'd like to mention before bringing everything to a close. The SVM requires that the inputs be fixed dimensions, so the "IsFace" implementation resizes the input image if it's too big or too small. If it's the wrong dimensions, though, then it leaves black bars above-and-below or left-and-right of the input (which is part of the process that I described in "Feature extraction for maybe-a-face images"). I found that the classification accuracy improved slightly if I expanded the maybe-a-face region so that it matched the aspect ratio of the SVM's input dimensions first. For example, if the skin tone pass identified a face region that was 91x241px and I knew that the SVM was configured to work with input images of 128x128px then I would first expand the 91x241px region to 241x241px (similarly, if I had a region that was 123x56px then I would expand it to 123x123px).
Performance
In the context of this kind of work, "performance" relates to two distinct areas - how accurately does it perform its work and how quickly does it do it? To an extent, the two are related since we could make the skin tone filter work more quickly (if we reduced the limit from no-input-dimension-may-be-more-than-400px to 300px or 200px) but at the risk of it no longer identifying regions that we want it to. As we've just seen with the SVM training, the time it takes to train it depends upon the quantity of data (both the size of the input image that features are extracted from and the number of input images) - so the inputs could be reduced (so that the training time would be shorter) but this negatively affects the accuracy of the classifier.
(A handy tip that I used when I was happy with the SVM training but experimenting with the skin tone pass was that the Accord.NET SVM class may be serialised using the BinaryFormatter - so I was persisting it to disk between runs, rather than having to re-train it on every run)
Once the SVM is trained, it is very quick at classifying. Which makes sense, since all it needs to do is take a feature set, apply its linear formula and see which side of the hyperplane the data point sits on. There is a little work required to extract the feature data from a maybe-face sub-image in order to give the SVM something to work on but it takes less then 15ms per sub-image on my computer. The skin tone pass is slower, taking between 150 and 300ms for the images that I've been testing with (which are all about 1000px on the largest side and so are resized down to 400px before being processed). I'd like to cut this time down because I like the idea of being able to apply this processing to video and I feel that it needs to be able to process at least five frames a second to convincingly track faces. I haven't made any effort towards this yet but reducing the total time down to 200ms feels reasonable since the code has been written to be easy to follow and tweak, rather than to be fast, so there is surely plenty of performance tuning potential.
Another reason that I haven't spent any time optimising the current code is that it might be wiser to spend time researching alternative algorithms. For example, Accord.NET has some support for face detection, such as the FaceHaarCascade class (which I believe is the same class of detector as the Viola–Jones object detection framework) -
Rectangle[] faceRegions;
using (var image = new Bitmap(path))
{
var detector = new HaarObjectDetector(new FaceHaarCascade());
faceRegions = detector.ProcessFrame(image);
}
However, it gave poor results for my images. It seemed to do well with very small faces but struggled with larger images (or the images where the faces took up a large proportion of the image). It's very possible that I could improve the accuracy by tweaking the parameters. If my images are too large, maybe they should just be shrunk down further before processing? That might help the false negative rate but I'm also concerned about the false positive rate and I'm not sure that shrinking the image first would help with that.

One approach that sounds very promising: if the SVM classifier is so fast and effective then maybe we should get rid of the skin tone processing altogether and just generate segments from all over the image, then filter them with the classifier. This is discussed and recommended by many people and is referred to as the "sliding window" approach (see Sliding Windows for Object Detection with Python and OpenCV, for example). The idea is that you pick a window size (eg. 50px if limiting the source image to no more than 400px on a side) and then start at the top left of the image and take that top-left 50x50px as the first sub-image to pass to the classifier. Then you move the window over a bit (say, 10px) and then use that as the second sub-image. Keep going until you can't go any further and then go back to the left but go down 10px - moving across then back-and-down until you have covered the entire image. Then do the same with some other window sizes (maybe 75px and then 100px), since you don't know whether the faces on an image are going to be small (relative to the size of the image) or large. This will give you many, many regions to classify - but that's no problem because linear SVM classification is very fast. Unfortunately, I did try this but I got an enormous false positive rate (as you can see here with Tiger - if you can make him out from behind all the green "this is a face!" boxes). Surely this approach can be made to work since it's so commonly presented as a solution to this problem.. it may just be that I need to tweak how the SVM is trained, maybe it needs more than 2,000 training images (though I did also try it with 10,000 training images and the results were not much better).

To return to the performance of the skin-tone-pass-following-by-(2k-image-trained-)SVM-classification model that I've talked about for most of this post; in terms of accuracy I'm very happy with it. In the test images that I've been using, there are zero false positives. There are a couple of false negatives but I think that they are understandable. The first obvious failing that it has is with a black-and-white photo - since the skin tone face detector looks for particular hues and saturations, it's not going to work on if there is no colour in the image. That's just a built-in limitation of the approach.

Another failure is with a face that is half hidden behind someone else (in the top right of this group photo). The skin tone face detector identifies the face but the SVM classifies it as not-a-face. Since the face is half-hidden, I think that this is acceptable.


Last but not least is this unfortunate guy who foolishly entered some sort of drinking contest. I don't know if he won but he doesn't look too good about it one way or the other. The red liquid erupting from his lips falls within the first phase's looks-like-skin-tones bounds, as you can see by looking at the skin mask image. Not only is his head tilted in the shot but the vomit-detected-as-skin means that his face isn't centered in the maybe-face region. So I'm not surprised that the SVM doesn't correctly classify it.
In summary, it's not perfect but I'm still very happy with the results.
Article references
I want to close this post off by linking to the sites and papers that helped me get to this point. It's been a fun journey and is hopefully only my first step on the machine learning track!
The "Naked People Skin Filter (Fleck & Forsyth)" and "Face Detection in Color Images" papers were amongst the first that I found that had easily understandable material (for a face detection novice) that didn't use a third party library in some way.
Once I had implemented the skin tone logic and was looking to improve the results, one of the articles that I found most inspiring (partly because it was so approachable) was "Machine Learning is Fun! Part 4: Modern Face Recognition with Deep Learning" (by Adam Geitgey). This talks about taking things to the next step and performing facial recognition - not just locating faces but also trying to identify who they are, against a known database. I haven't got to that advanced point yet but it's definitely something that I'd like to explore. The only thing that I would say about this article is that it doesn't go into a lot of depth about generating HOGs or normalising them or what sort of input image size and other parameters to use. He does link to some Python code that uses third party libraries in lieu of more details, though. Since I wanted to write C# and (ideally) only take C# dependencies this wasn't very helpful to me. The article itself, though, got me really excited about the possibilities and I enjoyed the guy's writing style (and intend to read the rest of his "Machine Learning is Fun" series).
An article that did go into the details was the "HOG Person Detector Tutorial" (by Chris McCormick). This was also really well written and very approachable. Although it talks about detecting a person in a photo, rather than a face, the principles are the same. The description of the HOG generation and normalisation really helped me clarify in my mind how it should all work. This article links to the original HOG person detector paper by Dalal and Triggs [PDF], which is full of research information and graphs and equations - so if you want to dig deep then this is the place to start!
The Triggs and Dalal paper state in the introduction that "For simplicity and speed, we use linear SVM as a baseline classifier throughout the study". Later on they mention that they tried a non-linear kernel but that "Replacing the linear SVM with a Gaussian kernel one improves performance by about 3%.. at the cost of much higher run times". If this "why is a linear SVM classifier appropriate" explanation feels too light for you then it is discussed in greater depth in "Why do linear SVMs trained on HOG features perform so well? [PDF].
Finally, I want to mention again the article "Kernel Support Vector Machines for Classification and Regression in C#" by Accord.NET's César Souza. Here, he introduces the SVM in a much more formal way than I've done here, he includes a video about "The Kernel Trick" (which is a simple yet mind-blowing way in which the linear kernel can be used to classify data that doesn't immediately look like it would work for), he talks about other kernels (aside from linear he also describes polynomial and gaussian) and he describes how the Sequential Minimal Optimization learning algorithm works. There's a lot of code and there's illustrated examples at the end. When I found this article fairly early on in my research, I recognised how much care had gone into preparing it but also knew that I needed something a little more beginner-level first! So I bookmarked it for future reference and now I think that I understand (almost all of) it. Hopefully, if you started off knowing nothing but have followed all the way through this post, then you will too!
Posted at 18:39
About
Dan is a big geek who likes making stuff with computers! He can be quite outspoken so clearly needs a blog :)
In the last few minutes he seems to have taken to referring to himself in the third person. He's quite enjoying it.
Recent Posts
- Hosting a DigitalOcean App Platform app on a custom subdomain (with CORS)
- (Approximately) correcting perspective with C# (fixing a blurry presentation video - part two)
- Finding the brightest area in an image with C# (fixing a blurry presentation video - part one)
- So.. what is machine learning? (#NoCodeIntro)
- Parallelising (LINQ) work in C#
Highlights
- Face or no face (finding faces in photos using C# and Accord.NET)
- When a disk cache performs better than an in-memory cache (befriending the .NET GC)
- Performance tuning a Bridge.NET / React app
- Creating a C# ("Roslyn") Analyser - For beginners by a beginner
- Translating VBScript into C#
- Entity Framework projections to Immutable Types (IEnumerable vs IQueryable)
Archives
- April 2025 (1)
- March 2022 (2)
- February 2022 (1)
- August 2021 (1)
- April 2021 (2)
- March 2021 (1)
- August 2020 (3)
- July 2019 (2)
- September 2018 (1)
- April 2018 (1)
- March 2018 (1)
- July 2017 (1)
- June 2017 (1)
- February 2017 (1)
- November 2016 (1)
- September 2016 (2)
- August 2016 (1)
- July 2016 (1)
- June 2016 (1)
- May 2016 (3)
- March 2016 (3)
- February 2016 (2)
- December 2015 (1)
- November 2015 (2)
- August 2015 (3)
- July 2015 (1)
- June 2015 (1)
- May 2015 (2)
- April 2015 (1)
- March 2015 (1)
- January 2015 (2)
- December 2014 (1)
- November 2014 (1)
- October 2014 (2)
- September 2014 (2)
- August 2014 (1)
- July 2014 (1)
- June 2014 (1)
- May 2014 (2)
- February 2014 (1)
- January 2014 (1)
- December 2013 (1)
- November 2013 (1)
- October 2013 (1)
- August 2013 (3)
- July 2013 (3)
- June 2013 (1)
- May 2013 (2)
- April 2013 (1)
- March 2013 (8)
- February 2013 (2)
- January 2013 (2)
- December 2012 (3)
- November 2012 (4)
- September 2012 (1)
- August 2012 (1)
- July 2012 (3)
- June 2012 (3)
- May 2012 (2)
- February 2012 (3)
- January 2012 (4)
- December 2011 (7)
- August 2011 (2)
- July 2011 (1)
- May 2011 (1)
- April 2011 (2)
- March 2011 (3)