Writing F# to implement 'The Single Layer Perceptron'
TL;DR
This picks up from my last post Learning F# via some Machine Learning: The Single Layer Perceptron where I described a simple neural network ("The Single Layer Perceptron") and took a C# implementation (from an article on the site Robosoup) and rewrote it into a style of "functional C#" with the intention of then translating it into F#. Trying to do that all in one post would have made for a very very long read and so part two, here, picks things up from that point.
I'm still an F# beginner and so I'm hoping that having the pain so fresh in my mind of trying to pick it up as a new language will make it easier for me to help others get started. I'm going to assume zero knowledge from the reader.
(I'm also going to try to dive straight right into things, rather than covering loads of theory first - I think that there are a lot of good resources out there that introduce you to F# and functional concepts at a more abstract level but I'm going to take the approach that we want to tackle something specific and we'll discuss new F# concepts only when we encounter them while trying to get this work done!)
Translating the code into F#
Visual Studio 2017 includes support for F# without having to install anything extra. To get started, create a new project of type Visual F# / Console Application. This will generate a Program.fs file that will let you build and run (it won't be anything very interesting if you run it but that doesn't matter because we're going rewrite the file from scratch!).
In the C# code from last time, the core logic was contained within a static method called "Go" within a static class. To set up the scaffolding for something similar in F# we'll use the following code:
open System;
let private Go (r: Random) =
"TODO: Implement this"
[<EntryPoint>]
let private Main _ =
Go (new Random(0)) |> ignore
0
In F#, functions are declared by the keyword "let" optionally followed by an accessibility modifier (eg. "private") followed by their name followed by their arguments followed by "=" followed by the function body.
The last line of the function body will be a value that is returned by the function (unlike C#, there is no need for an explicit "return" keyword).
Above, there is a function "Go" that takes a Random argument named "r" and that returns a string. The return type is not explicitly declared anywhere but F# relies upon type inference a lot of the time to make reduce the "syntactic noise" around declaring types where the compiler can work them out on its own. If you wanted reassurance that the type inference has worked as you expect then you can hover over the word "Go" and you'll see the following signature for the function -
val private Go : r:Random -> string
This confirms that the function "Go" takes an argument named "r" of type random and that it returns a string.
If we changed the "Go" function to this:
let private Go r =
"TODO: Implement this"
.. and then hovered over the word "Go" then we'd see the following signature:
val private Go : r:'a -> string
This essentially means that the type "r" is not fixed and that it may be any type because there is no way for the compiler to apply any restrictions to it based upon the code that it has access to. When comparing to C#, you might imagine that this would be equivalent to this:
private string Go(object r)
.. but it would actually be more accurate to think about it like a generic method - eg.
private string Go<T>(T r)
The difference isn't important right now it's worth bearing in mind.
There's also a function "Main" that takes a single string argument argument named "_" and that returns an int. Just looking at this code, you may imagine that "_" would also be of an unknown / generic type but if you hover to the word "Main" then you'll see this signature:
val private main : string [] -> int
F# has applied some extra logic here, based upon the fact that the function has been annotated with [<EntryPoint>] - this requires that the function matches the particular signature of string-array-to-string and you will get a compile error if you try to declare a function signature that differs from this.
The string array is a list of arguments passed to the compiled executable if called from the command line. This will never be of use in this program and so I've named that argument "_" to tell F# that I will never want to access it. I do this because F# will warn you if you have any unused arguments because it suggests that you have forgotten something (why specify an argument if you don't need it??). If you really don't care about one, though (as is the case here), if you give it an underscore prefix (or call it simply "_") then the compiler won't warn you about it.
In a similar vein, F# will warn you if you call a function and ignore its return value. If the idea is that all functions be pure (and so have no side effects) then a function is useless if you ignore its return value. In the scaffolding above, though, we just want to call "Go" (which will do some calculations and write a summary to the console) - we don't really care about its return value. To tell the compiler this, we use a special function called "ignore" that we pass the return value of the "Go" function to. The C# way to do this might look something like this:
ignore(Go(new Random(0)))
This is valid F# but it's criticised as having to be read "inside out". It's more common in F# to see it like this:
Go (new Random(0)) |> ignore
The "pipe forward" operator (|>) effectively means take the value on the left and use it as the last argument in the function on the right. Since "ignore" only takes one argument, the two versions above are equivalent.
If a function has more than one argument then the pipe operator only provides the last one. To illustrate this, consider the method "List.map" that takes two arguments; a "mapping" delegate and a list of items. It's very similar to LINQ's "Select" method. You could call it like this:
let numbers = [1;2;3]
let squares = List.map (fun x -> x * x) numbers
I'll breeze through some of the syntax above in a moment but the important point here is that there is a method that takes two arguments where the second is a list.
It could be argued that this syntax is back-to-front because you may describe this in English as:
given a list of values, perform an operation on each item (and return a new list containing the transformed - or "mapped" - values)
.. but the code puts things in the opposite order ("list of values" is mentioned last instead of first).
However, the pipe operator changes that -
let numbers = [1;2;3]
let squares = numbers |> List.map (fun x -> x * x)
The code now is able to say "here is the list, perform this operation on each value to provide me with a new list".
Because the pipe operator passes the value on the left as the last argument to the function on the right, F# often has list-based functions where the list is the last argument. This is often the opposite order to C# functions, where the "subject" of the operation is the commonly first argument.
Now, as promised, a quick rundown of F# syntax introduced above. The "let" keyword is very similar to C#'s "var" in that it use type inference to determine what type the specific reference should be. Unlike "var", though, you can't change the reference later on - eg.
let numbers = [1;2;3]
// Invalid! This "=" operator is treated as a comparison whose return value is ignored
// rather than this statement being a reassignment - the "numbers" reference is still
// a list with the values 1, 2 and 3 (a compiler warning will be displayed)
numbers = [1;2;3;4]
Because F# only allows you to set value in statements that include the "let" operator, it makes it easier for the F# compiler to know whether the code fragment:
a = b
is an assignment or a comparison - if it follows a "let" then it's always an assignment but otherwise it's a comparison.
This is unlike C# where the following is acceptable:
var numbers = new[] { 1, 2, 3 };
// This is allowed in C#
numbers = new[] { 1, 2, 3, 4 };
.. and this means that the C# compiler can't as easily tell whether the code fragment "a = b" is an assignment or a comparison and that is why C# has the assignment operator "=" and a separate equality comparison operator "==" (and why F# can use "=" as both the assignment operator and equality comparison operator).
The next thing to talk about is that F# allows you to declare a list of values using square brackets and semi-colons as the separators. So the below are similar (but not equivalent, as I'll explain) in C#
and F# -
var numbers = new List<int> { 1, 2, 3 }; // C#
let numbers = [1;2;3] // F#
The reason that they're similar and not identical is that the C# code uses the System.Collections.Generic.List<T> type, which is mutable (you can add, remove and replace items within a list). In F#, the list is immutable and so any operation (such as add, remove or replace) would return a new list reference, rather than mutating the existing list.
You may have noticed that semi-colons are not present at the end of each F# line in the examples above. That's because they are not required. F# uses whitespace (such as line returns and indenting) to determine when statements terminate and when they continue and so semi-colons are not used to specify where statements finish (unlike in C#, where they are).
Finally, there was a delegate shown in the above code -
(fun x -> x * x)
This is an anonymous function. The F# code:
let numbers = [1;2;3]
let squares = numbers |> List.map (fun x -> x * x)
is roughly the same as the following C# code:
var numbers = new[] { 1, 2, 3 };
var squares = numbers.Select(x => x * x);
It's not precisely the same since "numbers" in the F# code is an immutable list reference and in C# it's an array but it's close enough. The point is that the "fun" keyword is used to declare an anonymous function and that brackets are required around that function declaration in order to segregate that code and make it clear to the compiler that the function declaration should be considered as a single value that is being passed to the "List.map" function.
Declaring training data
In the C# perceptron code from last week, there was an array of Tuple values that contained each pair of inputs and the expected result -
var trainingData = new[]
{
Pattern(0.08, 0.94, true),
// .. more patterns
};
The "Pattern" function was just this:
private static Tuple<double[], bool> Pattern(double x, double y, bool output)
{
return Tuple.Create(new[] { x, y }, output);
}
The Tuple class is a very convenient way to represent small groups of values (such as an input array and the expected boolean output) but one thing that I don't like is that the properties are named "Item1", "Item2", etc.. rather than it being possible to give them more descriptive labels.
I could have defined a class to contain these values but that can involve a lot of boilerplate code (particularly if it's an immutable class, which would be my preference when creating classes that describe data that should be initialised once and never changed).
Fortunately, F# has a convenient way to describe data like this called "Records" - immutable types that may be defined using very little syntax, such as by pasting the following into the F# scaffolding from earlier, just after "Open System" -
type private Input = { Values: float list; Result: bool }
It is now possible to define an input list / output boolean object with properties name "Values" and "Result" like this:
let x = { Values = [0.08; 0.94]; Result = true }
The type of "x" is not explicitly specified in the code but the compiler will be able to match it to the Input type.
double vs float
Note that I've defined the "Values" property to be of type "float list" (which is equivalent to "list<float>" - which is also valid syntax in F#) as opposed to "double list". In C#, Double and double represent a "double-precision floating point number" while Single and float represent a "single-precision floating point number". In F#, float is a double-precision floating point number while float32 is a single-precision floating point number. So "float" in F# is the same as "double" in C#. To make things more confusing, you can also specify the type double in F# and it means the same as float in F# - however, type signatures in the F# library specify float when a double-precision floating point number is returned and so I'm specifying float to try to be consistent with other F# code. For example, the library function "Double.Parse" returns float according to intellisense.
This seems quite confusing to me (coming at this from C#) but I decided to try to be as F#-like as possible and so "float list" is what I'm using.
Back to declaring training data..
To declare all of the training data in F#, we want a list of patterns -
let trainingData = [
{ Values = [0.08; 0.94]; Result = true }
{ Values = [0.13; 0.95]; Result = true }
// .. more patterns
]
When declaring a list (items within square brackets), they may either be separated by semi-colons or by line returns. So, above, each pattern is on its own line and so no semi-colons need to separate them while the individual numbers within the "Values" lists do need semi-colon separators since there are no line returns to break them up.
In the C# code, the "Pattern" function specifically took two "x" and "y" arguments and so each Tuple had an "Item1" property which was an array with two elements. In the above code, there would be no compiler warning if I accidentally included a line where the pattern had more "Values" entries than the others. As a sanity check, we can include the following code after the "trainingData" list is declared -
let inputLengths =
trainingData
|> List.map (fun input -> input.Values.Length)
|> List.distinct
|> List.length
if (inputLengths > 1) then raise (Exception "Inconsistent pattern input lengths!")
There's a lot of piping here, which seems to be quite common in F# code. Hopefully, though, it illustrates how using the pipe operator allows code to be written in a more logical order. Here, we're saying:
- Take the trainingData list
- Construct a list where each entry in the new list corresponds to the number of inputs in a trainingData entry
- Build a new list from this by taking this list-of-input-lengths and excluding any duplicates
- If the list from step 3 has more than one entry then the trainingData must not have entries that all have the same number of inputs
If the "trainingData" has patterns which all have the same number of inputs then there should only be one unique input input-list-length. If some patterns had two inputs and some patterns had three inputs then we would get more than one unique input-list-length and that would not be good.
Since F# has a concept of "significant whitespace" (meaning that it uses line returns and indentation to indicate where expressions start and end, which is why semi-colons are not required to terminate lines), sometimes it can get a bit demanding about what it thinks it ok and what isn't. In the code above, if you tried to put the "trainingData" on the same line as the "let inputLengths =" and then have the pipe operator lines start underneath it then you will get cryptic errors such as "The block following this 'let' is unfinished". Using the format above not only means that your code will be more consistent with other F# "in the wild" but it also means that the compiler will understand it!
// The F# compiler is happy with this..
let inputLengths =
trainingData
|> List.map (fun input -> input.Values.Length)
|> List.distinct
|> List.length
// .. it is NOT happy with this..
let inputLengths = trainingData
|> List.map (fun input -> input.Values.Length)
|> List.distinct
|> List.length
(I would not have thought that putting "trainingData" on the same line as "let inputLengths =" would introduce any ambiguity but presumably doing similar things must do in some situations).
Translating the network-training code
The c# code that we ended up with last time for training a network looked like this:
const double learningRate = 0.1;
var finalResult = Enumerable.Range(0, int.MaxValue)
.Scan(
seed: new
{
Weights = new[] { r.NextDouble(), r.NextDouble() },
Bias = 0d,
GlobalError = double.MaxValue
},
func: (previousState, iteration) =>
{
var resultForIteration = trainingData.Aggregate(
seed: new { Weights = previousState.Weights, Bias = previousState.Bias, GlobalError = 0d },
func: (stateSoFar, pattern) =>
{
var output = Output(stateSoFar.Weights, stateSoFar.Bias, pattern.Item1) ? 1 : -1;
var localError = (pattern.Item2 ? 1 : -1) - output;
return new
{
Weights = UpdateWeights(stateSoFar.Weights, learningRate, localError, pattern.Item1),
Bias = stateSoFar.Bias + (learningRate * localError),
GlobalError = stateSoFar.GlobalError + Math.Abs(localError)
};
}
);
Console.WriteLine("Iteration {0}\tError {1}", iteration, resultForIteration.GlobalError);
return resultForIteration;
}
)
.First(state => state.GlobalError <= 0);
.. and relied upon the following two functions:
private static bool Output(double[] weights, double bias, double[] inputs)
{
var sum = inputs.Zip(weights, (input, weight) => input * weight).Sum() + bias;
return (sum >= 0);
}
private static double[] UpdateWeights(double[] weights, double learningRate, double localError, double[] inputs)
{
if (localError == 0)
return weights;
return weights
.Zip(inputs, (weight, input) => weight + (learningRate * localError * input))
.ToArray();
}
I'm going to start with translating the "Output" function first because it will be relatively straight forward but it will also demonstrate some interesting abilities of the F# compiler's type inference abilities.
Type inference means that there are a lot of types that you don't have to specify in F# code because the compiler will be able to work out what they are. But this can be confusing sometimes if you don't have a strong enough grasp on how the compiler does this.
Because I'm still an F# noob, I like to specify function arguments types to begin with and then remove them afterwards once I can see that the compiler is happy without them and when I understand how the compiler knows. So I'll start with this:
let Output (weights: float list) (bias: float) (inputs: float list) =
let sum = (List.zip weights inputs |> List.map (fun (weight, input) -> weight * input) |> List.sum) + bias
sum >= float 0
The brackets around the arguments are required to "group" the argument name and its type into one value. When we remove the type annotations shortly, the argument brackets will no longer be necessary.
The "List.zip" function is very similar to LINQ's "Zip" function except that it has no facility to take a delegate to combine the two values, instead it always returns a tuple for each pair of values that it combines.
(I didn't use the pipe operator with the "List.zip" call above because I think that it read more naturally without it in this case - I think of this as "zipping the weights and inputs lists together" and that is what the code says)
F# has nice support for tuples that allows us to avoid having to rely upon "Item1" and "Item2" accesses. The lambda above that performs multiplication would have to look something like this in C# if the input was a tuple:
weightAndInput => weightAndInput.Item1 * weightAndInput.Item2
.. but F# allows us to "deconstruct" the tuple by providing names for the tuple properties - ie.
fun (weight, input) -> weight * input
This is still a function that takes a single argument, it's just that that single argument is a two-item tuple and we're accessing its two items through named references "weight" and "input".
Hopefully the rest of the code is easy to understand, "List.zip" is like LINQ's "Zip" and "List.map" is like LINQ's "Select" and "List.sum" is like LINQ's "Sum".
The second line "sum >= float 0" is the return value for the function - either true or false. The expression "float 0" is important because the "sum" value will be a float and F# will not attempt any type coercion when comparing values. In C#, if you have two numeric types then you can compare them - eg.
// Valid in C#
double x1 = 0; // double
int x2 = 0; // int
var isMatch = (x1 == x2);
.. but in F# this is not allowed. If you tried to write the following:
// Not allowed in F#
let x1 = float 0 // float
let x2 = 0 // int
let isMatch = (x1 = x2)
.. then you would get the following error:
This expression was expected to have type 'float' but here has type 'int'
Now that we're happy with the function implementation, we can remove the type annotations and reduce it to this:
let Output weights bias inputs =
let sum = (List.zip weights inputs |> List.map (fun (weight, input) -> weight * input) |> List.sum) + bias
sum >= float 0
The compiler is able to infer all of those types. Some of the inference is quite simple - for example, both "weights" and "inputs" must be lists of some type because they are passed to "List.zip".
Some of the inference is more complicated, though..
Firstly, the "weights" and "inputs" list must have element types that support a "*" operator (in F#, this means any of the numeric types or any type that has got a custom "*" overload implemented on it).
Secondly, when elements are combined from "weight" and "inputs" using "*", it must be possible to use the "+" operator on the result because "List.sum" requires it (the internal implementation of "List.sum" is to combine all of the values passed to it using "+").
Thirdly, the result from "List.sum" must also support the "+" operator in conjunction with whatever type that "bias" is.
Fourthly, this result must support the ">=" operator in conjunction with "float 0".
Working backwards, because F# does not support any type coercion when comparing numeric values, the type of "sum" must be float in order for it to be compared to "float 0". This means that the result of "List.sum" must be float and so "bias" must be float. This means that the "weights" and "inputs" must be lists of float. (The return type of the function is boolean because the return value is always true or false as it is the result of an ">=" comparison).
This type inference is very powerful and can lead to clean and succint code. However, it can also lead to confusion if you haven't perfectly internalised its workings or if you're dealing with incomplete code. It's for both of those reasons that I prefer to start with more argument type annotations than necessary and then remove them later, when I'm happy with what I've written.
The "UpdateWeights" function may be translated in a similar manner -
let UpdateWeights weights localError inputs =
if (localError = float 0)
then weights
else
List.zip weights inputs
|> List.map (fun (weight, input) -> weight + (learningRate * localError * input))
In F#, if / then / else is a bit different to C#. In F#, it is an expression that returns a value, so you could write something like:
// Valid F#
let x = if something then 1 else 2
// Not valid C#
var x = if something then 1 else 2
So, in the F# "UpdateWeights" function, the "if" expression returns either the original "weights" reference or the updated list.
We've actually seen quite a lot of F# syntax, just in the code above - variable and function definitions, type annotations (and discussed how they are optional in many cases), anonymous functions (with the "fun" keyword), the pipe forward operator, record types, tuple deconstruction. Let's throw in another one; nested functions. The two functions shown above ("Output" and "UpdateWeights") will only be called from within the "Go" function that was part of the initial scaffolding code. We could make these private functions at the same level as "Go".. or we can make them nested functions within "Go" so that their scope is as restrictive as possible (which is a good thing in my book) -
let private Go (r: Random) =
let Output weights bias inputs =
let sum = (List.zip weights inputs |> List.map (fun (weight, input) -> weight * input) |> List.sum) + bias
sum >= float 0
let UpdateWeights weights localError inputs =
if (localError = float 0)
then weights
else
List.zip weights inputs
|> List.map (fun (weight, input) -> weight + (learningRate * localError * input))
"TODO: Implement this"
Sidebar: The influence of F# on C#
It seems that quite a lot of features from F# are coming over to C# from C# 7 onwards. For example, nested functions are already available (they weren't in C# 6 but they are in C# 7) - eg.
public static void Go()
{
int GetNumber()
{
return 123;
}
Console.WriteLine(GetNumber());
}
Similarly, Tuple deconstruction is also now available -
public static void Go()
{
var (inputs, output) = GetPattern();
Console.WriteLine(string.Join(", ", inputs));
Console.WriteLine(output);
}
// Note: We're not returning a "Tuple<double[], bool>" here, it's a different type (and it requires
// the "System.ValueType" package to be added to the project
private static (double[] inputs, bool output) GetPattern()
{
return (new[] { 0.5, 0.6 }, true);
}
Coming at some point (looks like it will be C# 8), there will be support for defining record types -
// This syntax is not yet available (as of January 2018)
public class Point(int X, int Y);
The Point class will have X and Y properties that are set through a constructor call. It will have an "Equals" implementation that will return true for two Point references that have the same X and Y values (and probably have == and != operator overloads that do the same thing) and it will have a "With" method that allows you to take an instance of a Point and create a new instance that has a new value for either X or Y - eg.
var p1 = new Point(1, 2);
var p2 = new Point(1, 2);
Console.WriteLine(p1 == p2); // True!
p2 = p2.With(X: 7);
Console.WriteLine(p1 == p2); // False
(For more details about C# record types, see the records proposal).
It's interesting to see these features working their way into C# and hopefully it will make it easier for someone in the future to try F# if they already know C#. (Some may argue that it could make F# less appealing with more of its features being added to C# but I think that it will still have enough differences to stand apart - having immutability and non-nulls by default is not something that is likely to be incorporated into C# because it would require enormous changes).
Back to translating the network-training code..
Now that the supporting functions ("Output" and "UpdateWeights") have been translated, we need to look back at the main training code. This time I'm going to go "outside in" and translate this:
const double learningRate = 0.1;
var finalResult = Enumerable.Range(0, int.MaxValue)
.Scan(
seed: new
{
Weights = new[] { r.NextDouble(), r.NextDouble() },
Bias = 0d,
GlobalError = double.MaxValue
},
func: (previousState, iteration) =>
{
// Do work here..
}
)
.First(state => state.GlobalError <= 0);
The "Enumerable.Range(0, int.MaxValue)" line was basically a way to say "keep enumerating for ever" (int.MaxValue isn't technically the same as "forever" but in this context it's good enough because we'll die of boredom waiting for the code to perform two billion iterations).
In F# there is a function that seems closer to what we want called "Seq.initInfinite" - this takes a single argument that is a delegate that takes an int and returns a value in the generated sequence based upon that int. It could be implemented in C# like this:
public static IEnumerable<T> InitInfinite<T>(Func<int, T> initialiser)
{
return Enumerable.Range(0, int.MaxValue).Select(initialiser);
}
This is also limited to int.MaxValue iterations since the delegate argument is an int but we're still not going to worry too much about whether it's really infinite or not.
From my last post, we know that "Scan" is already an F# concept and so that should be easy to translate.
The last function to translate is "First" and this has a corresponding function in F#; "Seq.find".
The only issue that we have to tackle now is that F# does not support anonymous types and so we'll need to declare another record type that I'll call "CalculationState".
type private CalculationState = {
Weights: List<float>
Bias: float
GlobalError: float
}
When I defined the "Input" record earlier, I used a single line definition and so each property had to be separated by semi-colons. Above, each property is on its line and so semi-colon delimiters are not required.
Now we can translate the above C# into this F#:
let finalResult =
Seq.initInfinite (fun i -> i)
|> Seq.scan
(fun previousState iteration ->
// Do work here..
)
{ Weights = [r.NextDouble(); r.NextDouble()]; Bias = float 0; GlobalError = Double.MaxValue }
|> Seq.find (fun state -> state.GlobalError = float 0)
The "// Do work here.." code looks like this in C# -
var resultForIteration = trainingData.Aggregate(
seed: new { Weights = previousState.Weights, Bias = previousState.Bias, GlobalError = 0d },
func: (stateSoFar, pattern) =>
{
var output = Output(stateSoFar.Weights, stateSoFar.Bias, pattern.Item1) ? 1 : -1;
var localError = (pattern.Item2 ? 1 : -1) - output;
return new
{
Weights = UpdateWeights(stateSoFar.Weights, learningRate, localError, pattern.Item1),
Bias = stateSoFar.Bias + (learningRate * localError),
GlobalError = stateSoFar.GlobalError + Math.Abs(localError)
};
}
);
Console.WriteLine("Iteration {0}\tError {1}", iteration, resultForIteration.GlobalError);
return resultForIteration;
I'm going to break this out into a separate function in the F# code because I want to avoid the final code being too "dense" (particularly while I'm still getting used to reading F# syntax and common structures / flow) so I'll change the F# outer code to this:
let finalResult =
Seq.initInfinite (fun i -> i)
|> Seq.scan
CalculateNextState
{ Weights = [r.NextDouble(); r.NextDouble()]; Bias = float 0; GlobalError = Double.MaxValue }
|> Seq.find (fun state -> state.GlobalError = float 0)
.. and then define this nested function:
let CalculateNextState (state: CalculationState) (iteration: int) =
// Do work here..
(Again, I've started by including explicit type annotations for the arguments but I'll be able to remove them later).
The C# code used the "Aggregate" function which corresponds to "List.fold" in F# and "Console.WriteLine" which corresponds to "printfn". With everything that we've covered already, it shouldn't be a big leap to see that the complete implementation of the "CalculateNextState" function will be as follows:
let CalculateNextState (state: CalculationState) (iteration: int) =
let resultForIteration =
List.fold
(fun stateSoFar input ->
let output = if (Output stateSoFar.Weights stateSoFar.Bias input.Values) then 1 else -1
let localError = float ((if input.Result then 1 else -1) - output)
{
Weights =
if (localError = float 0)
then stateSoFar.Weights
else UpdateWeights stateSoFar.Weights localError input.Values
Bias =
if (localError = float 0)
then stateSoFar.Bias
else stateSoFar.Bias + (learningRate * localError)
GlobalError = stateSoFar.GlobalError + Math.Abs(localError)
}
)
{ Weights = state.Weights; Bias = state.Bias; GlobalError = float 0 }
trainingData
printfn "Iteration %i\tError %i" iteration (int resultForIteration.GlobalError)
resultForIteration
It's still taking me a little while to get used to there being no "return" keyword and so I sometimes have to remind myself that the anonymous function passed to "List.fold" returns the { Weights, Bias, GlobalError } value and that the "CalculateNextState" function returns the "resultForIteration" that is on its last line.
Now that the function is fully defined, the type annotations can be removed from the "state" and "iteration" arguments. The "state" type is inferred because "List.fold" takes an initial value that has the properties Weights (float list) / Bias (float) / GlobalError (float) and the anonymous function also returns a value of that type and the only record type that matches those properties is "CalculationState". The "iteration" argument is inferred because it is used as an argument in the "printfn" call to populate a "%i" placeholder and "%i" placeholder values have to be integers.
Writing to console using printfn and "string interpolation"
You might have noticed that in the code above, the C# write-info-to-console line:
Console.WriteLine("Iteration {0}\tError {1}", iteration, resultForIteration.GlobalError);
was translated into this in F#:
printfn "Iteration %i\tError %i" iteration (int resultForIteration.GlobalError)
In principle, it's very similar; there are placeholders in the format string (which is what the "%i" values are in the F# code above) that will be populated with arguments passed to Console.WriteLine / printfn but there are a couple of key differences. The first is that the "%i% placeholder requires that the value used to populate it is an integer (alternatives are "%s" for strings, "%f" for floats and "%b" for booleans) but the second is much more exciting - the format string and the provided arguments are verified at compile time in the F# code whereas the C# code is only verified at run time. To make it really crystal clear what I mean by this, the following C# code will compile but fail when it's run -
// This will fail at runtime with "System.FormatException: 'Index (zero based) must be greater
// than or equal to zero and less than the size of the argument list.'" because there are two
// placeholders in the format string but only one value provided
Console.WriteLine("Hello {0}, {1}", "test");
On the other hand, the following F# won't even compile -
// Will refuse to compile: "This expression is a function value, i.e. is missing arguments."
printfn "Hello %s, %s" "test"
This makes me happy because I'm all about making the compiler catch simple mistakes instead of allowing them to surface at runtime.
Now, I will admit that I was using a somewhat old school method of writing messages there in C#. C#6 introduced its own interpretation of "string interpolation" that allows us to combine the "template string" with the placeholder values so that we don't accidentally include too many or too few placeholder value arguments. Instead of writing this:
// Old style
Console.WriteLine("Iteration {0}\tError {1}", iteration, resultForIteration.GlobalError);
.. we could write this:
// C# 6 string interpolation
Console.WriteLine($"Iteration {iteration}\tError {resultForIteration.GlobalError});
I would argue that this is even better again than the F# approach and it's unfortunate that F# doesn't currently have anything quite like this. That is one of the downsides to F# pioneering and pushing a lot of useful techniques that were later incorporated in to C#, I suppose!
(There is a proposal to add something similar to F# but it doesn't exist yet and I don't think that there is any suggestions that it will become available any time soon - see F# RFC FS-1001 - String Interpolation)
Sidebar: Selecting F# BCL functions
A little earlier, I nonchalantly said that
The C# code used the "Aggregate" function which corresponds to "List.fold" in F#
.. and you may (quite reasonably) have wondered how you or I were supposed to know that "Aggregate" in C# is equivalent to "fold" in F#.
You may also have picked up on the fact that sometimes I'm using "Seq" functions (such as "Seq.initInfinite") and sometimes I'm using "List" functions (such as "List.fold") and be wondering how I'm deciding which to use.
I'll address the second point first. As I do so, it's worth bearing in mind that I'm going to explain how I have been deciding up to this point and hopefully it's a sensible approach but there's always a chance that someone who knows better (maybe me in six months!) will have a slightly different take on things..
In a nutshell, I'm going to use "List" if I'm certain that I want to fully evaluate the set of items. In the "CalculateNextState" function, I want to take all of the weights in the current state and generate a completely updated set of weights to use in the next iteration - in that next iteration, I will be using all of the just-calculated weights to generate another completely updated set of weights. Every time, I will be considering every weight value and there would be no benefit to lazily evaluating the data and I think that lazy evaluation is one of the main benefits to using "Seq". When I don't know how many iterations will be required, I start by lazily evaluating an infinite set of items by calling "Seq.initInfinite" and then terminating enumeration when I get a state with a sufficiently low GlobalError. This approach only works because the sequence is evaluated "lazily" - it would make no sense for there to be a "List.initInfinite" because that list's contents would have to be fully populated at runtime and you'd run out of memory!
I suspect that a case could be made for always using "Seq" unless you find a compelling reason not to.. where a compelling case is that you need pattern matching* or if you're sure that using "Seq" is resulting in expensive operations being repeated because you are enumerating over a sequence multiple times and the operations in each enumeration are complex / expensive (if you used "List" then you would be sure that the work to build the list would only be done once, no matter how many times you enumerated over it).
* (which we haven't encountered yet but which is fairly common in F# code and which only works with instances of list and not of seq)
F# also supports arrays but these tend to used in fairly niche situations - such as when interoperating with other .NET code that requires an array or when you've found a performance bottleneck in your code relating to indexed access into your set of items (for both a seq and a list it's relatively slow to jump straight to the nth item because you have to start at the beginning and walk that many items into the list, whereas with an array you can jump straight there).. but arrays have their disadvantages, such as being mutable (bleurgh, filthy!) and having no cheap way to create a new version with a single new item (which also applies to seq but which is something that list can do well).
So (for now?) I'll be using a list if I have a known set of items and will be performing an operation on every item each iteration and a seq otherwise.. unless I encounter a really exciting reason to do otherwise*.
* (Spoiler alert: in a future post in the series, I will find a case where there is a huge difference in memory usage between list and array when loading data from disk - brace yourself for that thrill!)
To return to my first point in relation to "Selecting F# BCL functions" - how did I know that "List.fold" is equivalent to "Aggregate"? The simple answer is by looking through the docs.. the MSDN pages are pretty good (here is the one for List.fold) and the number of base library functions is not that large. You can often guess what many of them do (such as "List.average" and "List.distinct") but you might need to read the documentation for others (either on MSDN or just via the intellisense tooltips) for others. If you are familiar with LINQ then it shouldn't take you too long to learn the names of the F# equivalents of many of your old favourites!
Demonstrating the network's abilities
Before I went on a couple of tangents about writing to the console and learning the F# BCL, we had actually finished translating the code that trained the network (it may be an extremely simple one but it is still technically a network!). Now the only C# that remains to be translated is the code that passes pairs of inputs through the network to see what output it generates for each pair - just to ensure that it matches our expectations. This is how we left it last time:
const double startAt = 0;
const double endAt = 1;
const double increment = 0.25;
var range = Enumerable.Range(0, (int)((endAt - startAt) / increment) + 1).Select(value => value * increment);
var xyPairs = range.SelectMany(value => range, (x, y) => new[] { x, y });
Console.WriteLine(string.Join(
Environment.NewLine,
xyPairs.Select(inputs => $"{string.Join("\t", inputs)}\t{(Output(finalResult.Weights, finalResult.Bias, inputs) ? "Yes" : "No")}")
));
The first thing that will be nice about translating this into F# is that it has better support for defining ranges. In C#, we used "Enumerable.Range" but that only works with integers and so we then had to do some division. In F#, we're able to say "define a range by starting at x and incrementing by y until you get to z". So we could replace this:
const double startAt = 0;
const double endAt = 1;
const double increment = 0.25;
var range = Enumerable.Range(0, (int)((endAt - startAt) / increment) + 1).Select(value => value * increment);
.. with this:
let range = { float 0 .. float 0.25 .. float 1 }
We could then translate the rest of the C# shown above in a like-for-like fashion into F# or we could get a tiny bit fancier with some code that I found on Stack Overflow that takes one set of values and transforms it by combining every value with other value (so if your input set was the numbers 1 and 2 then the output would be {1,1} and {1,2} and {2,1} and {2,2}). This is sometimes referred to as taking the "cross product" and is the same concept as doing a "cross join" in SQL.
The code to do it is as follows:
// Inspired by https://stackoverflow.com/a/482922/3813189
let crossproductWithSelf xs = seq { for x1 in xs do for x2 in xs do yield x1, x2 }
Using this means that our "Display network generalisation" summary code looks like this:
let crossproductWithSelf xs = seq { for x1 in xs do for x2 in xs do yield x1, x2 }
let calculatedResults =
{ float 0 .. float 0.25 .. float 1 }
|> crossproductWithSelf
|> Seq.map (fun (x, y) ->
x.ToString() + ",\t" +
y.ToString() + ",\t" +
(if (Output finalResult.Weights finalResult.Bias [x; y]) then "Yes" else "No")
)
printfn ""
printfn "X,\tY,\tOutput"
printfn "%s" (String.concat Environment.NewLine calculatedResults)
Pretty neat and tidy, I think!
Done! What's next?
Phew! Well that felt like quite a lot of work. Getting to grips with a new language can be mentally taxing, particularly when it involves a new paradigm (like making the leap from OOP to functional programming) and I think that that's why it's taken me several attempts at getting started with F# to even get this far.
And although this is a good start, the "machine learning" aspect of the Single Layer Perceptron is very basic and it should be fun to try to dig a little deeper and attempt something more complicated. To that end, I have a few more posts that I'd like to write that will explain how to train a neural network (that has more layers than just the input and output layers) using the Backpropagation Algorithm and then use this to recognise handwritten digits from the famous MNIST image database.
As with the code here, I will be starting with C# from the Robosoup blog and translating it into a functional style before rewriting it as F#. I think that it's exciting stuff!
One more thing - in case you're curious to see the complete F# code that was scattered through this post, here it is:
open System
type private Input = { Values: list<float>; Result: bool }
type private CalculationState = {
Weights: List<float>
Bias: float
GlobalError: float
}
let Go (r: Random) =
let trainingData = [
{ Values = [0.08; 0.94]; Result = true }; { Values = [0.13; 0.95]; Result = true };
{ Values = [0.28; 0.66]; Result = true }; { Values = [0.3; 0.59]; Result = true };
{ Values = [0.31; 0.51]; Result = true }; { Values = [0.34; 0.67]; Result = true };
{ Values = [0.34; 0.63]; Result = true }; { Values = [0.36; 0.55]; Result = true };
{ Values = [0.38; 0.67]; Result = true }; { Values = [0.4; 0.59]; Result = true };
{ Values = [0.4; 0.68]; Result = true }; { Values = [0.41; 0.5]; Result = true };
{ Values = [0.42; 0.53]; Result = true }; { Values = [0.43; 0.65]; Result = true };
{ Values = [0.44; 0.56]; Result = true }; { Values = [0.47; 0.61]; Result = true };
{ Values = [0.47; 0.5]; Result = true }; { Values = [0.48; 0.66]; Result = true };
{ Values = [0.52; 0.53]; Result = true }; { Values = [0.53; 0.58]; Result = true };
{ Values = [0.55; 0.6]; Result = true }; { Values = [0.56; 0.44]; Result = true };
{ Values = [0.58; 0.63]; Result = true }; { Values = [0.62; 0.57]; Result = true };
{ Values = [0.68; 0.42]; Result = true }; { Values = [0.69; 0.21]; Result = true }
{ Values = [0.7; 0.31]; Result = true }; { Values = [0.73; 0.48]; Result = true };
{ Values = [0.74; 0.47]; Result = true }; { Values = [0.74; 0.42]; Result = true };
{ Values = [0.76; 0.34]; Result = true }; { Values = [0.78; 0.5]; Result = true };
{ Values = [0.78; 0.26]; Result = true }; { Values = [0.81; 0.48]; Result = true };
{ Values = [0.83; 0.32]; Result = true }; { Values = [0.83; 0.28]; Result = true };
{ Values = [0.85; 0.07]; Result = true }; { Values = [0.85; 0.45]; Result = true };
{ Values = [0.88; 0.4]; Result = true }; { Values = [0.89; 0.92]; Result = true };
{ Values = [0.9; 0.33]; Result = true }; { Values = [0.91; 0.05]; Result = true };
{ Values = [0.92; 0.44]; Result = true }; { Values = [0.95; 0.94]; Result = true };
{ Values = [0.96; 0.08]; Result = true };
{ Values = [0.02; 0.76]; Result = false }; { Values = [0.06; 0.22]; Result = false };
{ Values = [0.07; 0.16]; Result = false }; { Values = [0.09; 0.43]; Result = false };
{ Values = [0.1; 0.08]; Result = false }; { Values = [0.14; 0.07]; Result = false };
{ Values = [0.15; 0.23]; Result = false }; { Values = [0.17; 0.18]; Result = false };
{ Values = [0.17; 0.11]; Result = false }; { Values = [0.21; 0.28]; Result = false };
{ Values = [0.22; 0.17]; Result = false }; { Values = [0.25; 0.09]; Result = false };
{ Values = [0.28; 0.28]; Result = false }; { Values = [0.28; 0.27]; Result = false };
{ Values = [0.29; 0.22]; Result = false }; { Values = [0.29; 0.29]; Result = false };
{ Values = [0.3; 0.29]; Result = false }; { Values = [0.31; 0.14]; Result = false };
{ Values = [0.33; 0.19]; Result = false }; { Values = [0.33; 0.06]; Result = false };
{ Values = [0.39; 0.15]; Result = false }; { Values = [0.52; 0.1]; Result = false };
{ Values = [0.65; 0.07]; Result = false }; { Values = [0.71; 0.1]; Result = false };
{ Values = [0.74; 0.05]; Result = false }
]
let inputLengths =
trainingData
|> List.map (fun input -> input.Values.Length)
|> List.distinct
|> List.length
if (inputLengths > 1) then raise (Exception "Inconsistent pattern input lengths!")
let learningRate = 0.1
let Output weights bias inputs =
let sum = (List.zip weights inputs |> List.map (fun (weight, input) -> weight * input) |> List.sum) + bias
sum >= float 0
let UpdateWeights weights localError inputs =
if (localError = float 0)
then weights
else
List.zip weights inputs
|> List.map (fun (weight, input) -> weight + (learningRate * localError * input))
let CalculateNextState state iteration =
let resultForIteration =
List.fold
(fun stateSoFar input ->
let output = if (Output stateSoFar.Weights stateSoFar.Bias input.Values) then 1 else -1
let localError = float ((if input.Result then 1 else -1) - output)
{
Weights =
if (localError = float 0)
then stateSoFar.Weights
else UpdateWeights stateSoFar.Weights localError input.Values
Bias =
if (localError = float 0)
then stateSoFar.Bias
else stateSoFar.Bias + (learningRate * localError)
GlobalError = stateSoFar.GlobalError + Math.Abs(localError)
}
)
{ Weights = state.Weights; Bias = state.Bias; GlobalError = float 0 }
trainingData
printfn "Iteration %i\tError %i" iteration (int resultForIteration.GlobalError)
resultForIteration
let finalResult =
Seq.initInfinite (fun i -> i)
|> Seq.scan
CalculateNextState
{ Weights = [r.NextDouble(); r.NextDouble()]; Bias = float 0; GlobalError = Double.MaxValue }
|> Seq.find (fun state -> state.GlobalError = float 0)
let crossproductWithSelf xs = seq { for x1 in xs do for x2 in xs do yield x1, x2 }
let calculatedResults =
{ float 0 .. float 0.25 .. float 1 }
|> crossproductWithSelf
|> Seq.map (fun (x, y) ->
x.ToString() + ",\t" +
y.ToString() + ",\t" +
(if (Output finalResult.Weights finalResult.Bias [x; y]) then "Yes" else "No")
)
printfn ""
printfn "X,\tY,\tOutput"
printfn "%s" (String.concat Environment.NewLine calculatedResults)
Go (new Random(0))
Posted at 23:24
Learning F# via some Machine Learning: The Single Layer Perceptron
TL;DR
I know C# well and I want to learn F#. I want to wrap my head about some of the underlying algorithms that enable the machine learning that seems so prevalent in the world today (voice recognition, computer vision, sales prediction, semantic analysis, translation). I'm going to try to do both together and prove to myself that I have a good understanding of them both by writing about it.
The lure of F#
For a few years now, I've been wanting to have a proper crack at learning F#. There's a lot about it that sounds very appealing - immutability-by-default and better representation / handling of null values while still being able to use Visual Studio and use the .NET framework library (as well as other .NET assemblies). I've tried a couple of times in the past but without any concrete project to work on, I find that I struggle to motivate myself without a target to work towards that is more tangible than "feel like I've learned a bit of a new language".
To address this, I've decided to combine learning-some-F# with learning-some-machine-learning-basics so that I have a more solid goal. As I go, I thought that I'd write a few posts about the process for two reasons; firstly, being able to explain something clearly is a good indicator that you understand it yourself and, secondly, there is a chance (admittedly slim!) that this might be useful to someone else in a similar position to me, who is familiar with C# and wants to get to grips with F# - I wouldn't even consider myself intermediately competent yet and so I'm still encountering the pain points of being an F# beginner and seeing how I deal with them might be helpful to others.
Last year, I wrote Face or no face (finding faces in photos using C# and Accord.NET), which classified image regions using a linear support vector machine. This was technically a machine learning solution but it's only one particular algorithm and there are limitations to the sorts of problem that it can tackle. I want to work up to implementing a Back-Propagation Neural Network that will categorise hand written digits (0-9) but I'm going to start a little simpler.
While trying to decide how I was going to get started, I read (or scan-read, in many cases, if I'm being honest) what felt like hundreds of articles about neural networks. One of the issues with trying to learn something like this through the research of others is that the people writing about it already have a level of knowledge far above my own on the matter and it feels like there is a lot of knowledge that it assumed that the reader will have. Another issue is that there is often maths involved that can seem sufficiently complicated that it is off-putting. In my posts, I'm going to try to keep things as simple as possible (which may well mean brushing some "whys" under the carpet - leaving it as an exercise to the reader to find out more from other people, once the basics are understood). One series of posts that I did find very approachable, though, was on a site "Robosoup" - which is for a consultancy based in London that specialise in machine learning. The first post in the series is "The Single Layer Perceptron C#" and I'm actually going to start with some of the code there and the example data. I'm going to try to explain things my own way but much of the content here will owe a debt to that Robosoup article (I got in touch with John Wakefield at Robosoup and he said that he was happy for me share his code - rest assured that I'm not just stealing it without asking for permission first!).
The Single Layer Perceptron
The concept of an "artificial neural network" is, essentially, that there is a system of neurons that are connected together and that have a series of inputs that send signals into the system and which eventually get (somehow) transformed into a series of outputs. Each output represents a particular result. If, for example, the neural network was intended to categorise images then the inputs will all be derived from the image data in some way and there may be an output for "dog" and an output for "cat" and these output will end up with a stronger or weaker signal depending upon the input data. The connections between the neurons will have different "weights" and so different input values will somehow result in different outputs. These different weights will have to calculated as part of the network's "training". This sort of description is often accompanied by complicated-looking diagrams such as this:
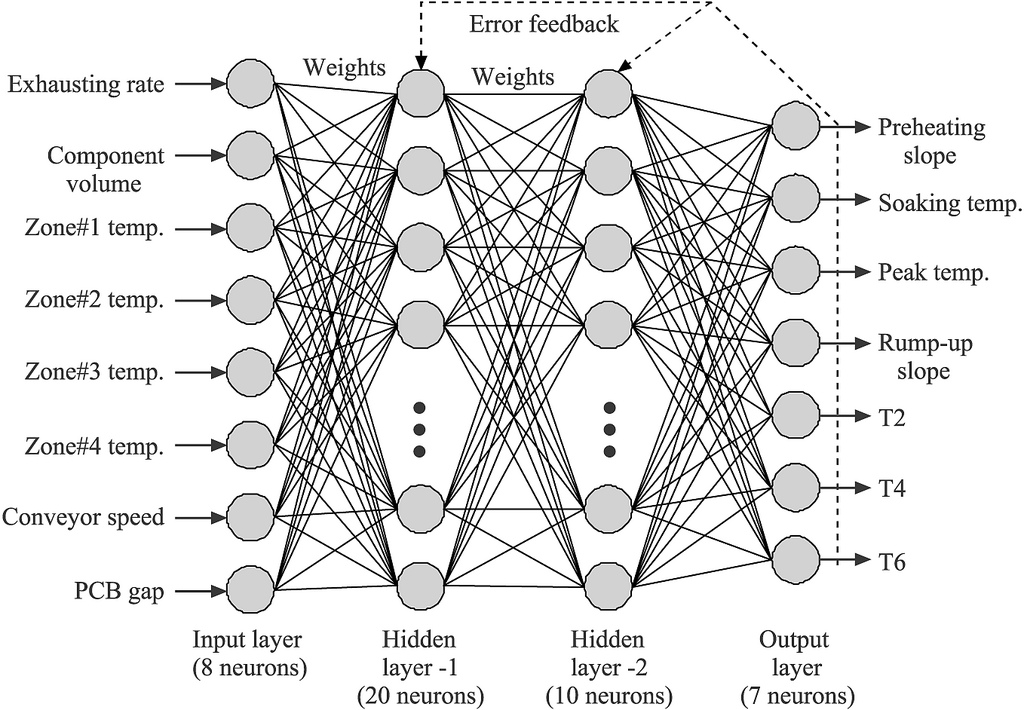
(Taken from Cesar Harada's Flickr under license conditions)
This raises a lot of questions and feels like far too complicated a place to start! (Though, in later posts, I will be talking about multi-layered multi-output neural networks similar to what is shown above).
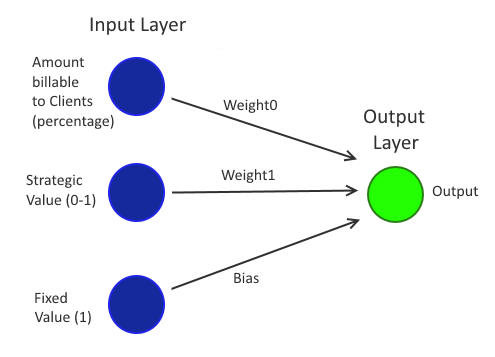
The "Single Layer Perceptron" is simpler - it only has one input "layer" and one output "layer", where a layer is a list of "neurons". A neuron is something that takes an input value (a value from -1 to 1), multiplies it by a "weight" (also a value from -1 to 1) and then passes that value onto every node that it is connected to in the layer ahead of it. Pretty much the simplest possible network imaginable that would fit this description would be just two neurons in the input layer and a single neuron in the output layer. Like this:
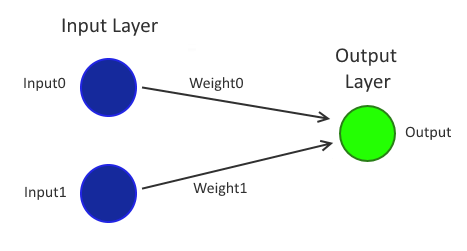
Now this might almost seem too simple! Can this really do anything useful? Well, actually, it's entirely possible to configure a network like this to act as a classifier for any data that is "linearly separable" in as many dimensions as there are inputs. This is already sounding like mumbo jumbo, so I'll go over those terms..
A "classifier" will look at its inputs and give a yes/no answer (for example, an "is this a cat?" classifier might look at a photograph and report whether there appears to be a cat in it or not).
"Linearly separable" is simplest to understand in 2D - if the data is plotted on a graph then it's "linearly separable" if it's possible to draw a straight line across the graph that puts all of the values for "yes" lie on one side and all inputs for "no" lie on the other side. When I wrote about linear support vector machines, I talked about a fictional decision history for a manager, where they would give the go-ahead (or not) to a new feature based upon how much of it could be billed to Clients and what strategic value it had to the company.
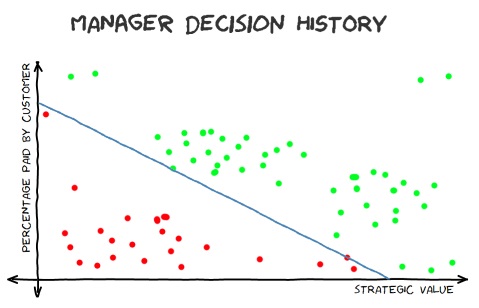
This data is linearly separable because it's possible to draw a line on the graph where all of the data above gets a "yes" response and all of the data below gets a "no".
Some data sets will not fit this model and so are not linearly separable. That won't make it impossible to classify using a neural network but it will make it impossible for a perceptron to classify (without some form of processing of the data before classification - which is out of the scope of what I want to cover today).
2D data like this would involve a perceptron with two inputs. 3D data that is linearly separable would have all of its data points separable by a plane in the 3D space - all points on one side would be "yes" and all points on the other would be "no"; this data would involve a perceptron with three inputs.
While it's not as easy to envisage this in more dimensions, the same principle holds. For this sort of multi-dimensional data, the additional dimensions tend to be additional measurable factors that are thought to have affected the outcome (for example, maybe the manager in the example above is predictably less likely to give the go-ahead to features on Monday and Tuesday because they're always snowed under with emails for those first two days of the week and they're less likely to sign off on things when they're hungry; that would mean that there would be four dimensions to consider, which would be "amount of cost that can be put onto Clients", "strategic value of the work", "day of the week" and "time since last ate" - these four dimensions would require a perceptron with four inputs to model the data).
Training a perceptron
I said above that it's possible to configure a network to act as a classifier for linearly separable data. All that is required to configure the network is to assign the weight0 and weight1 values (at least, that is the case for 2D data - since each input has its own weight value then 2D data requires two inputs but if the input is three dimensional then there will be three weight values that must be set and if there were four dimensions then there would be four weight values, etc..). When it is correctly configured, it will be possible to apply any values to the input neurons and to get a single output value. If this output value is higher than a particular threshold then the output will be considered a positive response and otherwise it will be considered a negative response.
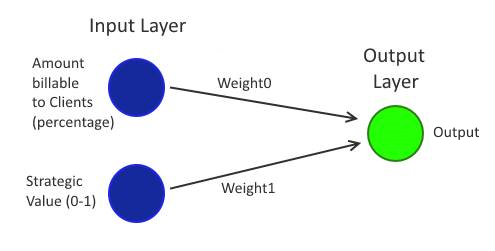
Returning to the Manager Decision data, one of the inputs will be for the "amount of cost that can be put onto Clients" while the other will be the "strategic value of the work". For the data and the code that I'm going to look at further down, all inputs and outputs are in the 0-1 range (this is convenient enough for "amount of cost that can be put onto Clients" but it may be more difficult in the real world to fit all features into a 0-1 range for "strategic value of the work" - but since that data is just a fictional example, we don't need to worry about that too much).
The question, then, is how should we determine the weights for each neuron? This is where the "machine learning" part comes into it. What we're going to do is "train" a network by using historical data.
At its essence, the way that a trained network like this is produced is by -
- Setting all of the weights to be random values between 0 and 1
- Passing all of the historical data (aka "training data") through it and, for each "pattern" (which is the name given to a series of inputs)
- Calculating the "local error" (the error for that particular pattern)
- Adjusting the weights based upon this local error
- Taking the "total error" or "global error" (the sum of all of the local errors from the training data) and either finding that it is less than a predetermined threshold (in which case the network training is considered complete - hurrah!) or going back to step 2
There are a lot of things to consider there - what precisely are the "local errors", how are the weights adjusted each iteration and what threshold should we stop at? Let's work through each of those in order..
The local error for a particular pattern is how far away the output of the network is from the expected result. Since all of the input data has a yes/no expected output, we'll translate "yes" into 1 and "no" into 0. For each pattern, we take its inputs and set the input neurons with those values. Then we calculate the output for the network (by multiplying the first input by the first weight and the second input by the second weight and then adding those two values together). Then we compare this output value to the expected 1 or 0 - so, if we get 0.3 as the output value for the first pattern and we expected 1 then that's an error of 0.7 (since 0.3 is 0.7 away from the expected value of 1). If we get 0.6 for the output value for the second pattern and we expected 0 then that's an error of 0.6 (since 0.6 is 0.6 away from the expected value of 0).
In order to adjust the weights after each pattern has been run through the network, a fairly simple equation is used - each new weight is calculated using:
weight[i] = weight[i] + (learningRate * localError * patternInput[i])
For this network, there are only two inputs and so there will only be two values for "i".
The "learning rate" is a value between 0 and 1 that determines how quickly the weights change as the network is trained. Clearly, a value of 0 would mean that the weights don't change each iteration, which would be useless. The larger the value of the learning rate, the more that the weights will be adjusted each iteration - however, larger is not always better because the adjustments may swing too far each time and, instead of slowing homing in on a well-trained network, the weights may alternate back and forth and never significantly improve. In the example code that I'm going to look at, I'm using a learning rate of 0.1* but this is a value that you may wish to try playing with when experimenting with training - there seem to be many guidelines when it comes to machine learning and many sensible approaches to classes or problem but there aren't always hard and fast rules for all of the variables and there are often things to tweak here and there that may affect how quickly you get a result (or if you get one at all).
* (To be honest, I've "decided" to use a learning rate of 0.1 because much of the initial C# code below comes from the Robosoup article that I mentioned earlier and a 0.1 learning rate is used there!)
The acceptable "global error" is another "tunable parameter" in that a higher acceptable threshold should mean that training will complete more quickly but also that the resulting network will be less accurate. On the other hand, it may be impossible to train a network (particularly so simple a network as a single perceptron) to match all of the training data perfectly and so a reasonable threshold must be accepted. In the example code below, a network that perfectly matches the training data is possible and won't take long to train and so we'll aim for a zero global error.
I'm not going to go into any more detail about how you may set these tunable parameters (learning rate and global error threshold) because there's a lot of material to cover and I want to try to stick to practical concepts and code (and because I'm still not very confident that I've got a great system for deciding them!).
Input bias
Using the training method described above, you will always get a line that cuts through the data at the point (0, 0). This would not work for the "Manager Decision History" graph because there is no way that a line starting at the bottom left of the graph could correctly cut through the data with all of the red points on one side and all of the green points on the other (on that graph all values are 0-1 and so the bottom left is the 0, 0 point).
A way to address this is to introduce an additional "bias" value. This is effectively like adding an additional neuron whose input value is always one and that has its own weight, just like every other input. Every time that a pattern is passed through the system while it is being trained, when the weights are adjusted, the bias should also be adjusted using the following formula:
bias = bias + (learningRate * localError)
(The formula is basically the same as the weight-adjusting formula except that the "patternInput[i]" value is removed because the bias neuron's input value is always 1)
This bias value means that the line that separates the yes/no values no longer has to go through (0, 0) but it has no other effect on training process, other than there being more slightly more work to do (although, without it, we wouldn't be able to get an answer for many sets of data - so it's not really more work at all!).
I've just said that it would not be possible to train a simple network of this form for some data sets without a bias.. which begs the question "for what data sets should a bias node be introduced?" - I think that it makes sense to always include one since, presumably, you don't know what solution the neural net should produce and so you don't know whether or not it would strictly be necessary to have a bias. So it's better to err on the safe side. If the data does not require a bias then the trained network should end up with a small (ie. close to zero) bias value and it will have little impact.
(This "input bias" is very different to moral biases that can creep into machine learning predictions due to biases, that are often unintentionally included, in the training data - see "Forget Killer Robots—Bias Is the Real AI Danger")
From C# to F#..
The format that I intend to follow for these posts is roughly as follows:
- Talk about the theory (we've already done that today!)
- Look at some fairly standard C# code
- Look at making the C# code more functional by removing variable mutations (including loops)
- Rewrite the "functional C#" in F#
As an F# beginner, this is the approach that I've been using for trying to learn it - until I've internalised it further, it still feels like a big ask to take regular C# and rewrite it into idiomatic F# and so the "functional C#" stage helps me a lot. The syntax of F# is not that big of a deal but thinking in (functional) F# is still something that I'm working towards.
(It's worth noting that, for me, getting my head around F# and functional programming is the priority. Much of the C# that we'll be looking will be doing in-place mutations - which, arguably, is a good model for doing the processing that we'll be looking at when it's done on a single thread - and since we'll be moving to using immutable structures then there is a good chance that the performance will be worse in the final F# code. If that turns out to be the case, though, then I'm not going to worry about it. I think that performance concerns are for when you have a better grasp of the technology that you're working with and I'm not there yet with F# - so I don't mind if I end up with worse-performing code in the context of this post so long as I've learned a lot from writing it!)
// Code slightly modified from that at
// http://www.robosoup.com/2008/09/the-single-layer-perceptron-c.html
public static class Perceptron
{
public static void Go(Random r)
{
// Load sample input patterns and expected outputs
var trainingData = new[]
{
Pattern(0.08, 0.94, true), Pattern(0.13, 0.95, true), Pattern(0.28, 0.66, true),
Pattern(0.3, 0.59, true), Pattern(0.31, 0.51, true), Pattern(0.34, 0.67, true),
Pattern(0.34, 0.63, true), Pattern(0.36, 0.55, true), Pattern(0.38, 0.67, true),
Pattern(0.4, 0.59, true), Pattern(0.4, 0.68, true), Pattern(0.41, 0.5, true),
Pattern(0.42, 0.53, true), Pattern(0.43, 0.65, true), Pattern(0.44, 0.56, true),
Pattern(0.47, 0.61, true), Pattern(0.47, 0.5, true), Pattern(0.48, 0.66, true),
Pattern(0.52, 0.53, true), Pattern(0.53, 0.58, true), Pattern(0.55, 0.6, true),
Pattern(0.56, 0.44, true), Pattern(0.58, 0.63, true), Pattern(0.62, 0.57, true),
Pattern(0.68, 0.42, true), Pattern(0.69, 0.21, true), Pattern(0.7, 0.31, true),
Pattern(0.73, 0.48, true), Pattern(0.74, 0.47, true), Pattern(0.74, 0.42, true),
Pattern(0.76, 0.34, true), Pattern(0.78, 0.5, true), Pattern(0.78, 0.26, true),
Pattern(0.81, 0.48, true), Pattern(0.83, 0.32, true), Pattern(0.83, 0.28, true),
Pattern(0.85, 0.07, true), Pattern(0.85, 0.45, true), Pattern(0.88, 0.4, true),
Pattern(0.89, 0.92, true), Pattern(0.9, 0.33, true), Pattern(0.91, 0.05, true),
Pattern(0.92, 0.44, true), Pattern(0.95, 0.94, true), Pattern(0.96, 0.08, true),
Pattern(0.02, 0.76, false), Pattern(0.06, 0.22, false), Pattern(0.07, 0.16, false),
Pattern(0.09, 0.43, false), Pattern(0.1, 0.08, false), Pattern(0.14, 0.07, false),
Pattern(0.15, 0.23, false), Pattern(0.17, 0.18, false), Pattern(0.17, 0.11, false),
Pattern(0.21, 0.28, false), Pattern(0.22, 0.17, false), Pattern(0.25, 0.09, false),
Pattern(0.28, 0.28, false), Pattern(0.28, 0.27, false), Pattern(0.29, 0.22, false),
Pattern(0.29, 0.29, false), Pattern(0.3, 0.29, false), Pattern(0.31, 0.14, false),
Pattern(0.33, 0.19, false), Pattern(0.33, 0.06, false), Pattern(0.39, 0.15, false),
Pattern(0.52, 0.1, false), Pattern(0.65, 0.07, false), Pattern(0.71, 0.1, false),
Pattern(0.74, 0.05, false)
};
// Randomise weights
var weights = new[] { r.NextDouble(), r.NextDouble() };
var bias = 0d;
// Set learning rate
var learningRate = 0.1;
var iteration = 0;
double globalError;
do
{
globalError = 0;
for (var p = 0; p < trainingData.Length; p++)
{
// Calculate output
var inputs = trainingData[p].Item1;
var output = Output(weights, bias, inputs[0], inputs[1]) ? 1 : -1;
// Calculate error
var expected = trainingData[p].Item2;
var localError = (expected ? 1 : -1) - output;
if (localError != 0)
{
// Update weights
for (var i = 0; i < 2; i++)
{
weights[i] += learningRate * localError * inputs[i];
}
bias += learningRate * localError;
}
// Convert error to absolute value
globalError += Math.Abs(localError);
}
Console.WriteLine("Iteration {0}\tError {1}", iteration, globalError);
iteration++;
} while (globalError != 0);
Console.WriteLine();
Console.WriteLine(
$"Final weights: {weights[0]}, {weights[1]}, Bias: {bias} => Error: {globalError}"
);
// Display network generalisation (note: the "Manager Decision" data has input values that
// are all in the range 0-1 in both dimensions and so we will only look at values in this
// range in this preview here)
Console.WriteLine();
Console.WriteLine("X,\tY,\tOutput");
for (double x = 0; x <= 1; x += .25)
{
for (double y = 0; y <= 1; y += .25)
{
var output = Output(weights, bias, x, y);
Console.WriteLine("{0},\t{1},\t{2}", x, y, output ? "Yes" : "No");
}
}
Console.WriteLine();
}
private static bool Output(double[] weights, double bias, double x, double y)
{
var sum = (x * weights[0]) + (y * weights[1]) + bias;
return (sum >= 0);
}
/// <summary>Helper for initialising training data</summary>
private static Tuple<double[], bool> Pattern(double x, double y, bool output)
{
return Tuple.Create(new[] { x, y }, output);
}
}
This code is fairly straightforward and it goes through the steps that I described before:
- Set weights to be random values and the bias to be zero
- Take each training data entry's input and calculate the output using the current weights (and bias), adjusting the weights (and bias) if the calculated output did not match the expected output
- Compare the total error against a threshold (of zero) and go back to step 2 if it's too high
The way that I'm going to change this code from "regular" (I would call it "object oriented" C# but the code shown here is probably closer to being "procedural") to "functional*" C# is by looking for things that would seem out of place in functional code and replacing them.
* ("functional" is often interpreted as meaning that you avoid side effects and avoid mutation - we can argue about that definition another day if you like but it's a good enough place to start for now!)
Immediately, the following things jump out at me:
- Variables whose values are explicitly changed during processing (eg. "iteration" and "globalError")
- Variables whose values change as part of looping constructs (eg. "i", "x" and "y")
- The do..while loop will not be useful if values are not to be mutated with it and so that will need to be replaced with something else
I suppose the question, then, is how can we possibly write code like this without changing / mutating / updating values?
The first thing to recognise is that LINQ made a more functional style of processing much more mainstream within C# and seem less alien. Before LINQ, if you had an array of values and you wanted an array containing the squares of these values (contrived example, I know, but bear with me) then you may well have achieved this in a fairly procedural manner - eg.
var values = new[] { 1, 2, 3 };
var squaredValues = new int[values.Length];
for (var i = 0; i < values.Length; i++)
squaredValues[i] = values[i] * values[i];
Each time the loop is executed, the value of "i" changes and the "squareValues" array is updated.
Until the for loop has been fully executed, the "squaredValues" array is only partially initialised.
Within the loop, it's technically possible to change the value of "i" and move it backwards or forwards (such as by throwing in a bonus "i++" to keep future code maintainers on their toes) and this can be the cause of potential coding errors in loops more complicated than the one shown here.
Since all we want to do is transform every single value in one array and create a new array from the results, it would be nice if we could be more descriptive in what we are trying to do and to remove some "book keeping" (such as tracking the "i" value using the for loop). This is what would happen if LINQ was used to perform the same work -
var values = new[] { 1, 2, 3 };
var squaredValues = values
.Select(value => value * value)
.ToArray();
Note that there is no mutation occurring here. Each time that the lambda that is passed to the "Select" method is called, a new "value" reference is created (unlike "i", which was a single variable shared across each iteration of the loop).
This is one technique that will be useful to remove mutation from code.
Another is the "Aggregate" method for enumerating a list of items and reducing it to a single reference. To try to illustrate; if I had a collection of words and I wanted to get the total number of words and the total number of letters then I might write procedural code like this:
static void ShowLetterAndWordCount(IEnumerable<string> words)
{
var numberOfLetters = 0;
var numberOfWords = 0;
foreach (var word in words)
{
numberOfLetters += word.Length;
numberOfWords++;
}
Console.WriteLine("Total number of letters: " + numberOfLetters);
Console.WriteLine("Total number of words: " + numberOfWords);
}
.. or I could achieve the same thing without any mutating variables by using the following code:
static void ShowLetterAndWordCount(IEnumerable<string> words)
{
var summary = words.Aggregate(
seed: new { NumberOfLetters = 0, NumberOfWords = 0 },
func: (valueSoFar, nextWord) => new
{
NumberOfLetters = valueSoFar.NumberOfLetters + nextWord.Length,
NumberOfWords = valueSoFar.NumberOfWords + 1
}
);
Console.WriteLine("Total number of letters: " + summary.NumberOfLetters);
Console.WriteLine("Total number of words: " + summary.NumberOfWords);
}
What "Aggregate" does is it takes a "seed" value and the first value of the list of items and combines them using the "func" lambda. It then takes this result and combines it with the second value of the list, also using the "func" lambda. It will then take this result and combines it with the third value of the list, etc.. until one final combined value is returned. In the code above, I've used an anonymous type for the seed (and so the final "summary" reference will also be an instance of that anonymous type and so have "NumberOfLetters" and "NumberOfWords" properties) but the seed can be a class or a primitive or any type that you need.
All of the "book keeping" required by the Aggregate method is handled by the method itself - there is no loop variable to worry about and there are no variables outside of the loop (such as "numberOfLetters" and "numberOfWords") that must be tracked. You need only to tell it what the initial "seed" value should be and how it should combine the "value so far" with a single item from the input list.
This is the advantage that it has over the procedural version (which may initially appear "less complicated") - you only need to consider what actually happens within a single operation and you don't have to look after any variables that must be maintained across the entire loop (which was the case with "numberOfLetters" and "numberOfWords" in the first version).
At its core, this means that the scope of variables is reduced and when they don't change (ie. they are immutable) there are less moving parts for you to mentally consider when trying to reason about any particular line of code.
I'm finding that the F# version of Aggregate (called "fold") is a very powerful and useful technique and so having a good grasp on how it works is very useful. Just to make it extra clear (apologies if this is belabouring the point but Aggregate doesn't, in my experience, tend to be commonly used in C# and so it may not be familiar to some), here's another example:
var values = new[] { 1, 2, 3, 4, 5 };
var sumOfValues = words.Aggregate(
seed: 0,
func: (valueSoFar, value) => valueSoFar + value
);
This will return 15 because it will just add all of the values together. It begins with a seed value of 0 and adds it to the first value (which is 1) to get 1. It then adds this "value so far" to the second value (which is 2) to get 3. It adds this to the third value (which is 3) to get 6 and adds this to the fourth value (which is 4) to get 10 and adds this to the fifth value (which is 5) to get 15.
Not a particularly useful piece of code - and one that could have been written more clearly as:
var values = new[] { 1, 2, 3, 4, 5 };
var sumOfValues = words.Sum();
.. but hopefully it reinforces how the Aggregate method operates on data. And hopefully it makes it clear how powerful Aggregate can be because so many other operations may be built on top of it, such as Min or Max -
static int? Min(IEnumerable<int> values)
{
return values.Aggregate(
seed: (int?)null,
func: (valueSoFar, nextValue) => (valueSoFar.HasValue && valueSoFar < nextValue)
? valueSoFar
: nextValue
);
}
static int? Max(IEnumerable<int> values)
{
return values.Aggregate(
seed: (int?)null,
func: (valueSoFar, nextValue) => (valueSoFar.HasValue && valueSoFar > nextValue)
? valueSoFar
: nextValue
);
}
To functional code.. one step at a time
Back to the Single Layer Perceptron code.. The way that I'm approaching this is to take one logical section of code and replace the procedural style of code with functional constructs.
The first that I'll tackle is the do..while loop and the mutation of the outer "iteration", "weights", "bias" and "globalError" variables.
This will be straightforward if we use the Aggregate method where the "value so far" contains a "Weights" array, a "Bias" value and a "GlobalError" value that will be re-calculated each iteration.
The input list passed to Aggregate will be an incrementing list of integers representing the current iteration number. The "func" lambda will take the previous Weights / Bias / GlobalError state and calculate the next Weight / Bias / GlobalError state. If the "previousState" already has a low enough GlobalError then the "func" lambda won't have to do any more calculating and can just return the previousState reference immediately (meaning that we don't have to do any more work and we can just let Aggregate finish as many iterations as it is configured to do so until the Aggregate call completes - if that sounds a bit unclear then hopefully it will make more sense after you see the code and I talk more about it below).
const double learningRate = 0.1;
const int maxNumberOfIterationsToPerform = 100; // See notes below code
var finalResult = Enumerable.Range(0, maxNumberOfIterationsToPerform)
.Aggregate(
seed: new
{
Weights = new[] { r.NextDouble(), r.NextDouble() },
Bias = 0d,
GlobalError = double.MaxValue
},
func: (previousState, iteration) =>
{
// The network is already trained - no more calculations required
if (previousState.GlobalError == 0)
return previousState;
var weights = previousState.Weights;
var bias = previousState.Bias;
var globalError = 0d;
for (var p = 0; p < trainingData.Length; p++)
{
// Calculate output
var inputs = trainingData[p].Item1;
var output = Output(weights, bias, inputs[0], inputs[1]) ? 1 : -1;
// Calculate error
var expected = trainingData[p].Item2;
var localError = (expected ? 1 : -1) - output;
if (localError != 0)
{
// Update weights (taking a copy of the weights array rather than altering its values)
weights = weights.ToArray();
for (var i = 0; i < 2; i++)
{
weights[i] += learningRate * localError * inputs[i];
}
bias += learningRate * localError;
}
// Convert error to absolute value
globalError += Math.Abs(localError);
}
Console.WriteLine("Iteration {0}\tError {1}", iteration, globalError);
return new { Weights = weights, Bias = bias, GlobalError = globalError };
}
);
(You may notice that I also changing "learningRate" from being a variable to be a const - since this will never change, it makes sense).
I've had to make a compromise in how I've written this code - I've had to specify a "maxNumberOfIterationsToPerform" value because the Aggregate method has no way to say "stop processing now, we have an answer that we're happy with". This is why there is the check at the top of the "func" lambda that says "if previousState's GlobalError is low enough then do no more calculation" - the Aggregate method will keep running through every single value in the input list. But how do we know that 100 iterations will be enough to get a zero Global Error? We don't!
What would be really helpful would be if we could have a variation of Aggregate that returns an IEnumerable of all of the intermediate calculation states (all of the "previousState" values) so that we could stop enumerating as soon as one of them has a GlobalError of zero - that way we wouldn't have to limit ourselves to a low maxNumberOfIterationsToPerform value. Something that would let us write code like this:
const double learningRate = 0.1;
var finalResult = Enumerable.Range(0, int.MaxValue)
.AggregateAndReturnIntermediateStates(
seed: new
{
// Same as in earlier code sample..
},
func: (previousState, iteration) =>
{
// Same as in earlier code sample but without the need to check GlobalError..
}
)
.First(state => state.GlobalError == 0);
I searched through the LINQ and the F# library documentation and I couldn't find anything in LINQ that I could use to do this but I did find something in F# called "scan". To implement it as a LINQ-esque C# extension method, though, is simple. If we start by considering what an implementation of Aggregate would look like:
public static TAccumulate Aggregate<TSource, TAccumulate>(
this IEnumerable<TSource> source,
TAccumulate seed,
Func<TAccumulate, TSource, TAccumulate> func)
{
var valueSoFar = seed;
foreach (var value in source)
valueSoFar = func(valueSoFar, value);
return valueSoFar;
}
.. we need only to change the return type from TAccumulate to IEnumerable<TAccumulate> and to throw in some "yield return" magic to produce "Scan":
public static IEnumerable<TAccumulate> Scan<TSource, TAccumulate>(
this IEnumerable<TSource> source,
TAccumulate seed,
Func<TAccumulate, TSource, TAccumulate> func)
{
yield return seed;
var valueSoFar = seed;
foreach (var value in source)
{
valueSoFar = func(valueSoFar, value);
yield return valueSoFar;
}
}
This means that I can now write:
const double learningRate = 0.1;
var finalResult = Enumerable.Range(0, int.MaxValue)
.Scan(
seed: new
{
// Same as in earlier code sample..
},
func: (previousState, iteration) =>
{
// Same as in earlier code sample (but still without the need to check GlobalError)..
}
)
.First(state => state.GlobalError == 0);
Hurrah! That's a good step forward!
Now I need to tackle the inner section:
var weights = previousState.Weights;
var bias = previousState.Bias;
var globalError = 0d;
for (var p = 0; p < trainingData.Length; p++)
{
// Calculate output
var inputs = trainingData[p].Item1;
var output = Output(weights, bias, inputs[0], inputs[1]) ? 1 : -1;
// Calculate error
var expected = trainingData[p].Item2;
var localError = (expected ? 1 : -1) - output;
if (localError != 0)
{
// Update weights (taking a copy of the weights array rather than altering its values)
weights = weights.ToArray();
for (var i = 0; i < 2; i++)
{
weights[i] += learningRate * localError * inputs[i];
}
bias += learningRate * localError;
}
// Convert error to absolute value
globalError += Math.Abs(localError);
}
Console.WriteLine("Iteration {0}\tError {1}", iteration, globalError);
return new { Weights = weights, Bias = bias, GlobalError = globalError };
I'm going to start from the inside and work outward this time. The first thing that I want to get rid of is the loop that is used to update weights. What this loop is effectively doing is walking through two arrays ("weights" and "inputs") and performing an operation on a single pair of items from each (each loop iteration, we do something with one weight value and one input value).
This is just what the "Zip" LINQ function does and so we can use that here. We'll replace:
// Update weights (taking a copy of the weights array rather than altering its values)
weights = weights.ToArray();
for (var i = 0; i < 2; i++)
{
weights[i] += learningRate * localError * inputs[i];
}
.. with this:
weights
.Zip(inputs, (weight, input) => weight + (learningRate * localError * input))
.ToArray();
To maker the "inner section" simpler, I'm going to hide that logic into a function:
private static double[] UpdateWeights(double[] weights, double learningRate, double localError, double[] inputs)
{
if (localError == 0)
return weights;
return weights
.Zip(inputs, (weight, input) => weight + (learningRate * localError * input))
.ToArray();
}
I've also pulled the "is localError zero" check into the method. It feels a little unnecessary when there are only two weights and two inputs but this new version of the weight-updating code may be called with any number of inputs and so it may make sense to avoid looping through them all when the localError is zero (because we won't be making any changes to the weights in that case).
The next thing to do is to get rid of the other for-loop and the values that it mutates on each iteration. This part:
var weights = previousState.Weights;
var bias = previousState.Bias;
var globalError = 0d;
for (var p = 0; p < trainingData.Length; p++)
{
// Apply current pattern and alter weights, bias and globalError accordingly..
}
If we group the "weights / bias / globalError" values into a single value then we can replace this with an Aggregate call, like we saw earlier:
var resultForIteration = trainingData.Aggregate(
seed: new { Weights = previousState.Weights, Bias = previousState.Bias, GlobalError = 0d },
func: (stateSoFar, pattern) =>
{
// Apply current pattern and calculate new weights, bias and globalError values..
// .. and return new object wrapping these values
return new { Weights = newWeights, Bias = newBias, GlobalError = newGlobalError },
}
);
Before I pull it all together, I want to make a small change to the "Output" function - the current version only works if there are precisely two inputs and two weights but the "UpdateWeights" function from a moment ago works with any number of inputs and so I think that "Output" should too. So we'll replace this:
private static bool Output(double[] weights, double bias, double x, double y)
{
var sum = (x * weights[0]) + (y * weights[1]) + bias;
return (sum >= 0);
}
.. with this:
private static bool Output(double[] weights, double bias, double[] inputs)
{
var sum = inputs.Zip(weights, (input, weight) => input * weight).Sum() + bias;
return (sum >= 0);
}
(Note that using "Zip" again means that we don't have to resort to any for loops)
Combining all of this, the network-training code becomes the following:
const double learningRate = 0.1;
var finalResult = Enumerable.Range(0, int.MaxValue)
.Scan(
seed: new
{
Weights = new[] { r.NextDouble(), r.NextDouble() },
Bias = 0d,
GlobalError = double.MaxValue
},
func: (previousState, iteration) =>
{
var resultForIteration = trainingData.Aggregate(
seed: new { Weights = previousState.Weights, Bias = previousState.Bias, GlobalError = 0d },
func: (stateSoFar, pattern) =>
{
var output = Output(stateSoFar.Weights, stateSoFar.Bias, pattern.Item1) ? 1 : -1;
var localError = (pattern.Item2 ? 1 : -1) - output;
return new
{
Weights = UpdateWeights(stateSoFar.Weights, learningRate, localError, pattern.Item1),
Bias = stateSoFar.Bias + (learningRate * localError),
GlobalError = stateSoFar.GlobalError + Math.Abs(localError)
};
}
);
Console.WriteLine("Iteration {0}\tError {1}", iteration, resultForIteration.GlobalError);
return resultForIteration;
}
)
.First(state => state.GlobalError <= 0);
The final piece of the puzzle is to change the "Display network generalisation" code to remove the for loops from there too -
for (double x = 0; x <= 1; x += .25)
{
for (double y = 0; y <= 1; y += .25)
{
var output = Output(weights, bias, new[] { x, y });
Console.WriteLine("{0},\t{1},\t{2}", x, y, output ? "Yes" : "No");
}
}
The natural thing would seem to be to replace those loops with Enumerable.Range calls.. however, "Range" only works int values and we need to use double in order to increment by 0.25 each time. We could write a new "Range" extension method that would take double values or we could just workaround the limitation. If we want the values 0, 0.25, 0.5, 0.75, 1 then that's five distinct values. The number of items may be calculated by taking the end value, subtracting the start value, dividing by the increment and then adding one (to ensure that we get the start value and the end value).
In this case, that would be ((1 - 0) / 0.25) + 1 = 4 + 1 = 5.
We can do that in code like this:
const double startAt = 0;
const double endAt = 1;
const double increment = 0.25;
var range = Enumerable.Range(0, (int)((endAt - startAt) / increment) + 1)
.Select(value => value * increment);
We then want to "cross join" range with itself so that we loop through every (x, y) combination. We can do that with creative use of "SelectMany" -
var xyPairs = range.SelectMany(value => range, (x, y) => new[] { x, y });
And now that nested for-loop may be replaced by this:
const double startAt = 0;
const double endAt = 1;
const double increment = 0.25;
var range = Enumerable.Range(0, (int)((endAt - startAt) / increment) + 1)
.Select(value => value * increment);
var xyPairs = range.SelectMany(value => range, (x, y) => new[] { x, y });
Console.WriteLine(string.Join(
Environment.NewLine,
xyPairs.Select(inputs => $"{string.Join("\t", inputs)}\t{(Output(finalResult.Weights, finalResult.Bias, inputs) ? "Yes" : "No")}")
));
That's the final piece of the convert-to-functional-code puzzle. Now we just need to translate it into F#!
Sidebar: "Function" vs "Method"
I find that in languages that are thought to be object oriented, the words "function" and "method" are commonly used interchangeably. Since beginning to become interested in so-called "functional programming", I've tried to find out whether there is a definitive or accepted difference between the two (after all, it's called functional programming rather than methodical programming, so surely someone thought that there was a difference!).
A few times, I've heard that the difference is that a "function" should not have any side effects and so should always return the same value given the same inputs. On the other hand, a "method" may cause side effects or rely upon ambient references - if the code writes to disk or reads DateTime.Now then it's not "pure" (where "pure" means that it relies only upon its arguments and does not produce any side effects - it only produces a return value and does not manipulate anything else) and so should be described as being part of a method rather than part of a function. Most recently I've seen it described in this Software Engineering Stack Exchange answer.
I try to use the word "function" only when it is known to be a pure function and a "method" otherwise (when it either definitely causes / relies upon side effects or if it's not clear). I still get it wrong from time to time (for example, I've been referring to LINQ "methods" in this post and we can probably presume that they are pure functions in most cases) but I'm still in the process of trying to internalise this terminology while I'm trying to internalise writing a more "functional" style of code for writing F#.
Writing F# code
If you've read this far then you may be detecting an unexpectedly abrupt end to the post judging by your browser's scrollbar!
Originally, I had intended to include all of the above content and go into how precisely to translate the functional C# code into F# but it quickly became clear that the post would be insanely large (I've written my fair share of monster posts in the past and I think that the time has come to put an end to them - this one's already pretty hefty).
Cliffhanger!
Sorry.
My next post will jump straight into F#. I will assume zero prior knowledge of the language itself but I also want to proceed at a decent rate. Hopefully this will mean that you won't get bored if you already have a little exposure to F# (or maybe it will be the worst of both worlds and be too slow for F# novices but too fast for those who've never seen it before). Let's wait and see*!
* (Should you be desperately excited and dying for part two, rest assured that it's already written and just needs a thorough proof-read - so it should be published early next week at the latest)
I'm not sure how many posts there will be in the series in total but the Single Layer Perceptron is just the first model that I want to cover before moving onto the Back Propagation Neural Network model and then onto the Multi-Output variation (which will be necessary in order to classify hand written digits from 0-9 as opposed to being a simple yes/no classifier). Although I said that performance is not my primary concern for this playing-with-F# process, there are a couple of interesting things that I'd like to talk about on that front. So there should be a lot to come over the next few months!
Posted at 22:18
About
Dan is a big geek who likes making stuff with computers! He can be quite outspoken so clearly needs a blog :)
In the last few minutes he seems to have taken to referring to himself in the third person. He's quite enjoying it.
Recent Posts
- Hosting a DigitalOcean App Platform app on a custom subdomain (with CORS)
- (Approximately) correcting perspective with C# (fixing a blurry presentation video - part two)
- Finding the brightest area in an image with C# (fixing a blurry presentation video - part one)
- So.. what is machine learning? (#NoCodeIntro)
- Parallelising (LINQ) work in C#
Highlights
- Face or no face (finding faces in photos using C# and Accord.NET)
- When a disk cache performs better than an in-memory cache (befriending the .NET GC)
- Performance tuning a Bridge.NET / React app
- Creating a C# ("Roslyn") Analyser - For beginners by a beginner
- Translating VBScript into C#
- Entity Framework projections to Immutable Types (IEnumerable vs IQueryable)
Archives
- April 2025 (1)
- March 2022 (2)
- February 2022 (1)
- August 2021 (1)
- April 2021 (2)
- March 2021 (1)
- August 2020 (3)
- July 2019 (2)
- September 2018 (1)
- April 2018 (1)
- March 2018 (1)
- July 2017 (1)
- June 2017 (1)
- February 2017 (1)
- November 2016 (1)
- September 2016 (2)
- August 2016 (1)
- July 2016 (1)
- June 2016 (1)
- May 2016 (3)
- March 2016 (3)
- February 2016 (2)
- December 2015 (1)
- November 2015 (2)
- August 2015 (3)
- July 2015 (1)
- June 2015 (1)
- May 2015 (2)
- April 2015 (1)
- March 2015 (1)
- January 2015 (2)
- December 2014 (1)
- November 2014 (1)
- October 2014 (2)
- September 2014 (2)
- August 2014 (1)
- July 2014 (1)
- June 2014 (1)
- May 2014 (2)
- February 2014 (1)
- January 2014 (1)
- December 2013 (1)
- November 2013 (1)
- October 2013 (1)
- August 2013 (3)
- July 2013 (3)
- June 2013 (1)
- May 2013 (2)
- April 2013 (1)
- March 2013 (8)
- February 2013 (2)
- January 2013 (2)
- December 2012 (3)
- November 2012 (4)
- September 2012 (1)
- August 2012 (1)
- July 2012 (3)
- June 2012 (3)
- May 2012 (2)
- February 2012 (3)
- January 2012 (4)
- December 2011 (7)
- August 2011 (2)
- July 2011 (1)
- May 2011 (1)
- April 2011 (2)
- March 2011 (3)